← Ana Rapor / YAMAN ÖZKAN / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
13 December 2025, 05:54
Bitiş
Devam ediyor
Süre
17 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Üçgen
  • Üçgen İnşası
Kazanımlar:
  • Matematiksel araç ve teknoloji yardımıyla düzlemde iki noktada kesişen çember çiftinin merkezleri ve kesişim noktalarından biri ile inşa edilen üçgenlerin kenar özelliklerine yönelik muhakeme yapabilme

Detaylı Değerlendirme

Genel Değerlendirme
Öğrenci, üçgenlerin iç açıları toplamı ve açılarına göre sınıflandırılması gibi temel konularda bilgi sahibidir. Basit ve doğrudan hesaplama gerektiren soruları doğru yanıtlayabilmektedir. Ancak, bu temel bilgileri daha karmaşık, cebirsel ifade içeren problemlere uygulama ve geometrik inşa gibi soyut ve kurala dayalı konseptleri anlama konusunda belirgin zorluklar yaşamaktadır.

Öğrencinin İyi Olduğu Konular
Öğrenci, aşağıdaki konularda başarılı bir performans göstermiştir:
- Üçgenlerin Açı Özellikleri: Bir üçgenin iç açılarının toplamının 180° olduğunu anladığını göstermiştir. İki açısı verilen bir üçgenin üçüncü açısını doğru bir şekilde hesaplayabilmektedir.
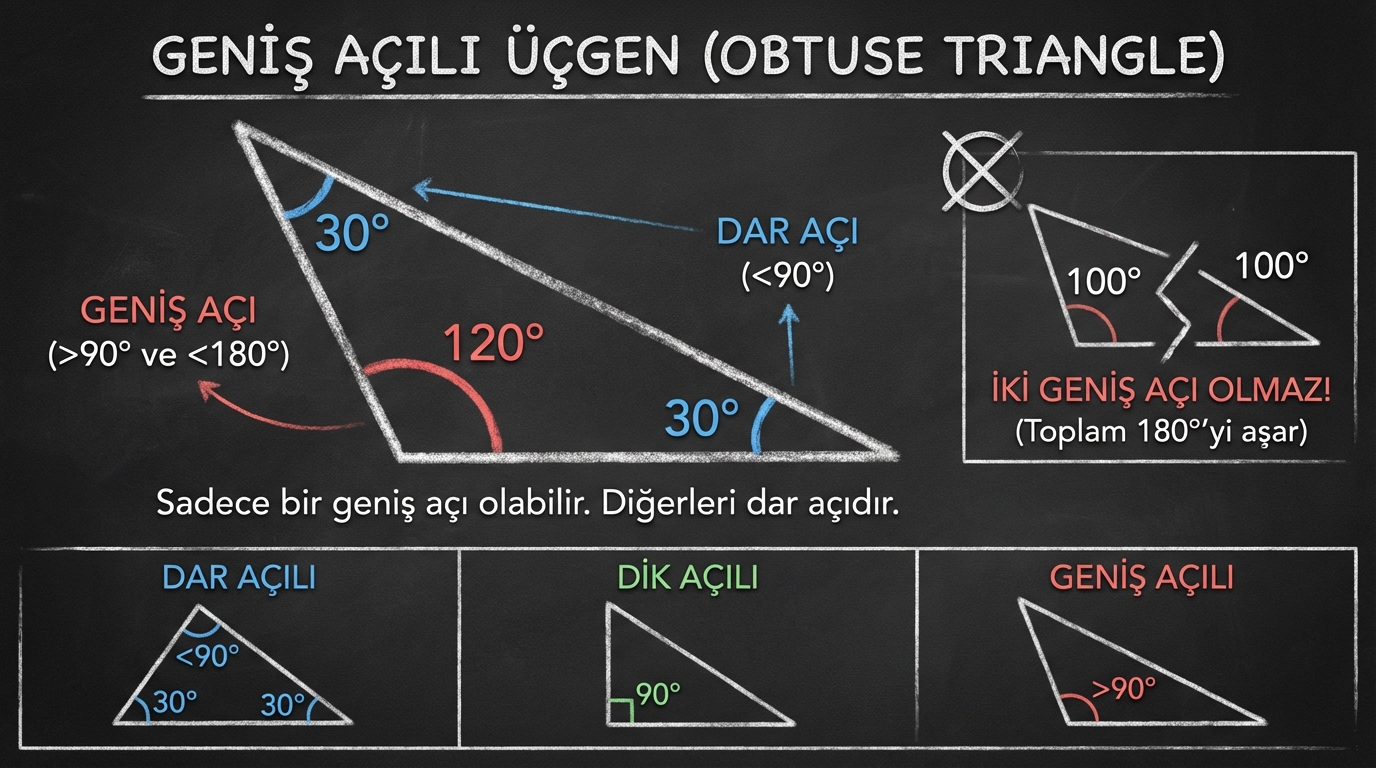
- Açılarına Göre Üçgen Çeşitleri: Verilen açılara göre bir üçgenin dar, dik veya geniş açılı olup olmadığını doğru bir şekilde tanımlayabilmektedir. Özellikle bir üçgende neden iki dik açı olamayacağını mantığıyla birlikte açıklamıştır.

Öğrencinin Eksik Olduğu Konular
Öğrencinin ders sırasında zorlandığı ve yanlış cevaplar verdiği konular şunlardır:
- Üçgen (Problem Çözme): Üçgenin iç açıları toplamı bilgisini, içinde bilinmeyen ve cebirsel ifade barındıran bir probleme uygulamada başarısız olmuştur. En büyük açısı 110° olan ve diğer iki açı arasında oransal bir ilişki bulunan soruyu yanlış çözmüştür. Bu durum, temel bilgiyi problem çözme becerisine aktarmada eksiklik olduğunu göstermektedir.
- Üçgen İnşası: Geometrik inşanın temel mantığını anlamakta zorlanmıştır. "Ölçüsüz cetvel" kullanımının amacını kavrayamamış ve pergel ile uzunluk taşıma prensibini gözden kaçırmıştır. Sorulan soruda, geometrik inşadaki bir hatayı tespit etmesi istenirken, konunun ana fikrinden uzaklaşarak sayısal bir cevap vermiştir. Bu, konunun kavramsal temelinde eksiklik olduğunu göstermektedir.

Ders Dışı Soru/Yorum
- Derste tamamen konu dışı bir soru veya yorum kaydedilmemiştir.

📜 Oturum Detayları

05:54:56
Öğrenci
Evet, hazırım Hocam! Bu konuyu detaylıca anlatır mısın?
05:54:57
💭 AI Öğretmen
Harika, başlıyorum
05:55:00
AI Öğretmen
Üçgen, üç tane kenarı ve üç tane köşesi olan kapalı bir şekildir.
05:55:02
AI Öğretmen
Bir üçgenin köşelerindeki açıların ölçüsüne bakarak, farklı türlerde üçgenler olduğunu görebiliriz.
05:55:04
AI Öğretmen
Bu türlerden biri de dik açılı üçgendir.
05:55:05
AI Öğretmen
Bir dik açılı üçgende, köşelerden yalnızca bir tanesinin ölçüsü $90°$ olur.
05:55:06
AI Öğretmen
$90°$ olan açıya dik açı adı verilir.
05:55:07
AI Öğretmen
Örneğin bir defterin köşesi, bir dik açıya örnek olarak düşünülebilir.
05:55:09
AI Öğretmen
Eğer bir üçgende bir köşe böyleyse, yani $90°$ ise, o üçgen dik açılı üçgendir.
05:55:11
AI Öğretmen
Bir üçgende iki tane dik açı olamaz çünkü üçgenin iç açıları toplandığında $180°$ etmelidir.
05:55:15
AI Öğretmen
Eğer iki açı $90°$ olsaydı, $90° + 90° = 180°$ olurdu ve üçüncü açıya hiç yer kalmazdı.
05:55:16
AI Öğretmen
Bu yüzden bir üçgende sadece bir tane dik açı olabilir.
05:55:17
AI Öğretmen
Buraya kadar olan kısmı anladın mı?
05:56:31
Öğrenci
Anladım
05:56:34
💭 AI Öğretmen
Güzel, devam edelim
05:56:34
❓ Soru medium
Aslı, bir üçgenin iç açılarından ikisinin 90° olabileceğini iddia ediyor ve böyle bir üçgen çizmeye çalışıyor. Aslı'nın bu iddiasının geometrik olarak neden yanlış olduğunu üçgenin iç açıları toplamı kuralını kullanarak açıklayınız. Eğer bir üçgenin iki açısı gerçekten 90° olsaydı, üçüncü açının ölçüsü kaç derece olurdu ve bu durum neden bir üçgen oluşturmazdı?
05:57:20
Öğrenci
Cevabım: 0 derece olurdu bu yüzden üçgenin diğer köşesi olmazdı
05:57:21
💭 AI Öğretmen
Hemen Bakıyorum
05:57:25
AI Öğretmen
Harika bir cevap! Tam isabet!
05:57:26
AI Öğretmen
Üçgenin iç açılarının toplamının 180° olması kuralını çok iyi kavramışsın.
05:57:28
AI Öğretmen
Eğer iki açı 90° olsaydı, üçüncü açının 0° olması gerektiğini ve bunun da bir üçgen oluşturamayacağını doğru bir şekilde belirttin. Aferin!
05:57:28
AI Öğretmen
Derse devam edelim mi?
05:57:45
Öğrenci
Olur, devam edelim
05:57:46
💭 AI Öğretmen
Güzel, devam edelim
05:57:53
AI Öğretmen
Dar açılı üçgen, üçgenlerin açılarına göre yapılan bir sınıflandırmadır.
05:57:54
AI Öğretmen
Bir üçgenin üç köşesindeki açıların hepsi 90 dereceden küçükse, bu üçgen dar açılı üçgen olur.
05:57:56
AI Öğretmen
Yani böyle bir üçgende her açı hem sivri hem de dardır.
05:57:59
AI Öğretmen
Hiçbir köşe 90 dereceye eşit olamaz ve hiçbiri 90 dereceden büyük olamaz.
05:58:01
AI Öğretmen
Bir üçgenin yalnızca bir veya iki açısı dar ise bu üçgen dar açılı olmaz; tüm açılar dar olmalıdır.
05:58:03
AI Öğretmen
Eğer üçgenin iki açısı dar, bir açısı dik açıysa bu bir dik üçgen olur, dar açılı üçgen sayılmaz.
05:58:04
AI Öğretmen
Kısacası bir üçgenin dar açılı sayılması için üç açısı da küçük ve sivri olmalı, 90 dereceden büyük veya eşit açı olmamalıdır.
05:58:05
AI Öğretmen
Dar açılı üçgenlerle ilgili anlattıklarımızı anladın mı?
05:58:37
Öğrenci
Anladım
05:58:42
💭 AI Öğretmen
Pekala, güzel
05:58:42
❓ Soru medium
Bir üçgenin iç açılarından ikisinin ölçüsü 55° ve 65°'dir. Bu üçgenin açılarına göre türünü belirleyiniz ve nedenini açıklayınız.
05:59:34
Öğrenci
Cevabım: Dar açılı üçgen olur çünkü bütün açılar dar
05:59:34
💭 AI Öğretmen
Hemen Bakıyorum
05:59:37
AI Öğretmen
Harika bir cevap! Tebrikler!
05:59:39
AI Öğretmen
Üçüncü açıyı (60°) doğru bir şekilde buldun ve tüm açıların 90 dereceden küçük olduğunu fark ederek üçgenin dar açılı olduğunu doğru belirttin.
05:59:41
AI Öğretmen
Bu, bir üçgenin iç açılarının toplamının 180° olduğunu ve dar açılı üçgenin tanımını çok iyi anladığını gösteriyor.
05:59:42
AI Öğretmen
Bu bilgileri kullanarak farklı üçgen türlerini kolayca belirleyebilirsin!
05:59:43
AI Öğretmen
Dolayısıyla doğru cevap dar açılı üçgendir.
05:59:43
AI Öğretmen
Derse devam edelim mi?
06:00:06
Öğrenci
Olur, devam edelim
06:00:08
💭 AI Öğretmen
Hmm
06:00:17
Görsel
Görsel
06:00:20
AI Öğretmen
Bir üçgenin açılarından biri 90 dereceden büyükse bu üçgene geniş açılı üçgen denir.
06:00:21
AI Öğretmen
Geniş açı, 90 derece ile 180 derece arasında ölçüsü olan açı anlamına gelir, bu yüzden geniş açılı üçgenlerin bir köşesi düz ve diğerlerinden daha geniş görünür.
06:00:24
AI Öğretmen
Bir üçgende iç açıların toplamı 180 derece olduğundan, bir üçgende iki geniş açı olamaz çünkü iki geniş açı toplanınca 180 dereceyi bulur ya da aşar ve üçüncü açı için yer kalmaz.
06:00:26
AI Öğretmen
Bu nedenle geniş açılı üçgenlerde sadece bir iç açı geniş olabilir ve kalan iki açı mutlaka dar açı olmalıdır.
06:00:29
AI Öğretmen
Geniş açılı üçgenler, bir üçgendeki açı ölçülerine göre yapılan sınıflandırmada, dar açılı ve dik üçgenlerle birlikte temel üçgen çeşitlerinden biridir.
06:00:30
AI Öğretmen
Geniş açılı üçgenlerle ilgili bu açıklamayı anladın mı?
06:01:15
Öğrenci
Anladım
06:01:19
💭 AI Öğretmen
Güzel, şimdi ilerleyelim
06:01:19
❓ Soru medium
Bir KLM üçgeni geniş açılı bir üçgendir. Bu üçgenin en büyük açısının ölçüsü 110°'dir. Diğer iki açıdan birinin ölçüsü diğerinin 3 katından 10° fazla olduğuna göre, bu üçgenin en küçük açısı kaç derecedir?
06:04:04
Öğrenci
Cevabım: 20
06:04:05
💭 AI Öğretmen
Hemen Bakıyorum
06:04:10
AI Öğretmen
Cevabınız doğru değil, çünkü üçgenin iç açılarının toplamı her zaman 180°'dir.
06:04:13
AI Öğretmen
Burada en büyük açı 110° olduğuna göre, diğer iki açının toplamı 180° - 110° = 70° olmalıdır.
06:04:14
AI Öğretmen
Diğer iki açıdan küçük olanına x dersek, büyük olan açı 3x + 10° olur. Bu yüzden denklemi x + (3x + 10) = 70 olarak kurarız.
06:04:17
AI Öğretmen
Denklemi çözdüğümüzde 4x + 10 = 70, yani 4x = 60 ve x = 15 bulunur. Bu da en küçük açının 15° olduğunu gösterir.
06:04:19
AI Öğretmen
Muhtemelen toplam açıların 180° olduğunu ve verilen ifadeyi denklem olarak kurmayı atlamış olabilirsiniz.
06:04:21
AI Öğretmen
Örnek olarak, eğer küçük açı 15° ise, diğer açı 3*15 + 10 = 55°, toplamları da 70° yapar; 110° ile toplandığında 180° olur.
06:04:21
AI Öğretmen
Bu yüzden doğru cevap en küçük açı için 15° olmalıdır.
06:04:22
AI Öğretmen
Derse devam edelim mi?
06:05:11
Öğrenci
Olur, devam edelim
06:05:13
💭 AI Öğretmen
Tamam, devam edelim
06:05:23
AI Öğretmen
Her tür üçgende geçerli olan temel bir kural vardır: Üçgenin iç açılarının toplamı daima $180^\circ$'dir.
06:05:25
AI Öğretmen
Bu kural, üçgenin dar açılı, dik açılı ya da geniş açılı olması fark etmeksizin, her zaman geçerlidir.
06:05:26
AI Öğretmen
Yani bir üçgenin üç iç açısını topladığımızda, sonuç mutlaka $180^\circ$ olur.
06:05:27
AI Öğretmen
Eğer bir üçgende iki iç açının ölçüsünü biliyorsak, bu iki açının ölçülerini toplarız.
06:05:28
AI Öğretmen
Topladığımız bu değeri $180^\circ$'den çıkararak, üçüncü açının ölçüsünü bulabiliriz.
06:05:31
AI Öğretmen
Bir üçgende eğer bir iç açı $90^\circ$ ise, o üçgen dik üçgendir.
06:05:32
AI Öğretmen
Üç iç açının hepsi $90^\circ$'den küçükse, bu üçgene dar açılı üçgen denir.
06:05:33
AI Öğretmen
Bir iç açı $90^\circ$'den büyükse, o üçgen geniş açılı üçgendir.
06:05:35
AI Öğretmen
Sonuç olarak, üçgenin tipi ne olursa olsun, iç açılarının toplamı her zaman $180^\circ$'dir ve bu tüm üçgenlerde ortak bir özelliktir.
06:05:36
AI Öğretmen
Üçgenlerin iç açılarının toplamının neden her zaman 180 derece olduğunu anladın mı?
06:06:23
Öğrenci
Anladım
06:06:27
💭 AI Öğretmen
Güzel, devam edelim
06:06:27
❓ Soru medium
Bir ABC üçgeninde A açısının ölçüsü 62° ve B açısının ölçüsü 48°'dir. Ali, C açısının ölçüsünü bulmak için şu işlemi yapmıştır: Önce 62 ile 48'i toplayarak 110 bulmuş, sonra da 180'den 110'u çıkararak sonucu 80° olarak hesaplamıştır. Ancak Ali'nin çıkarma işleminde bir hata vardır. Ali'nin hatasını düzelterek C açısının doğru ölçüsünü bulunuz ve bu üçgenin açılarına göre türünü (dar açılı, dik açılı, geniş açılı) belirtiniz.
06:07:05
Öğrenci
Cevabım: 70 derece çıkar ve dar açılı olur
06:07:06
💭 AI Öğretmen
Hemen Bakıyorum
06:07:09
AI Öğretmen
Harika bir iş çıkardın! C açısının ölçüsünü ve üçgenin türünü doğru buldun!
06:07:11
AI Öğretmen
Bir üçgenin iç açılarının toplamı her zaman 180°'dir ve tüm açıları 90°'den küçükse o üçgen dar açılıdır.
06:07:12
AI Öğretmen
Bu temel bilgileri kullanarak çok güzel bir çözüm yaptın, tebrikler!
06:07:14
AI Öğretmen
Bu nedenle, C açısı 70° ve üçgen dar açılıdır.
06:07:14
AI Öğretmen
Derse devam edelim mi?
06:07:34
Öğrenci
Olur, devam edelim
06:07:36
💭 AI Öğretmen
Güzel, devam edelim
06:07:40
Görsel
Görsel
06:07:42
AI Öğretmen
Geometrik inşa, sayıların doğrudan kullanılmadığı, sadece belirli araçlar kullanılarak şekillerin oluşturulduğu bir yöntemdir.
06:07:45
AI Öğretmen
Bu yöntemde, uzunluklar “5 cm, 7 cm” diye ölçülmez, bunun yerine verilen bir uzunluk, açı ya da konum; kullanılan araçlar sayesinde başka bir yere taşınır veya tekrar elde edilir.
06:07:46
AI Öğretmen
Geometrik inşada amaç, bize verilen şartlara göre doğru ve tam bir şekil oluşturmaktır ve burada yalnızca çizim kurallarına uyulur.
06:07:47
AI Öğretmen
Bu tür inşalarda iki önemli araç vardır.
06:07:48
AI Öğretmen
Pergel, çember çizmek için ve bir noktadan alınan bir uzunluğu başka bir noktaya taşımak için kullanılır.
06:07:51
AI Öğretmen
Pergelin açıklığını bir kez ayarladığınızda, bu büyüklükte aralıkları istediğiniz kadar tekrar tekrar işaretleyebilirsiniz.
06:07:53
AI Öğretmen
Ölçüsüz cetvel ise yalnızca doğru çizmek için kullanılır, cetvelin üzerindeki sayı ya da ölçü işaretleri dikkate alınmaz.
06:07:53
AI Öğretmen
Ölçüsüz cetvelle iki noktayı birleştiren düz çizgiler çizilir.
06:07:55
AI Öğretmen
Böylece pergel ve ölçüsüz cetvel beraber kullanılarak, sayı kullanmadan, sadece çizim ve çemberlerin özelliklerinden faydalanarak üçgen gibi şekiller oluşturulabilir.
06:07:57
AI Öğretmen
Geometrik inşanın en önemli noktası, çemberlerin ve doğruların kesiştiği yerlerden yeni noktalar elde ederek, istediğimiz üçgenleri oluşturabilmektir.
06:07:57
AI Öğretmen
Bu kısmı anladın mı, yoksa üzerinde durmamı istediğin bir nokta var mı?
06:09:05
Öğrenci
Anladım
06:09:09
💭 AI Öğretmen
Güzel, devam edelim
06:09:09
❓ Soru medium
Bir matematik projesinde, Elif'in görevi sadece pergel ve ölçüsüz cetvel kullanarak bir üçgen çizmektir. Elif çizime başlarken ilk olarak cetvelin üzerindeki santimetre işaretlerini kullanarak 8 cm uzunluğunda bir doğru parçası çizer ve bunu üçgenin ilk kenarı olarak belirler. Elif'in bu ilk adımı, metinde anlatılan geometrik inşa kurallarına göre neden hatalıdır ve bu kenarı doğru bir şekilde çizmek için ne yapmalıydı?
06:10:12
Öğrenci
Cevabım: 7cm
06:10:12
💭 AI Öğretmen
Hemen Bakıyorum
06:10:18
AI Öğretmen
Cevabınız yanlış, çünkü sadece bir sayı vermişsiniz ve Elif'in yaptığı hatayı açıklamamışsınız.
06:10:19
AI Öğretmen
Elif'in hatası, ölçüsüz cetveli bir ölçüm aracı gibi kullanmasıdır. Geometrik inşada cetvel üzerindeki santimetre işaretleri kullanılmaz, sadece düz çizgi çizmek için kullanılır.
06:10:22
AI Öğretmen
Doğru yöntem, pergel kullanarak verilen uzunluğu ölçmeden kopyalamaktır. Pergelin uçlarını başlangıç doğru parçasının uçlarına yerleştirip, bu aralığı bozmadan yeni bir noktaya taşıyarak yay çizmelidir.
06:10:23
AI Öğretmen
Bu şekilde uzunluk sayısal olarak ölçülmeden, sadece geometrik araçlarla doğru şekilde taşınmış olur. Bu temel kuralı unutmamak önemli.
06:10:24
AI Öğretmen
Bu yüzden doğru cevap, Elif'in ölçüsüz cetveldeki işaretleri kullanmaması ve pergeli bu şekilde kullanması gerektiğidir.
06:10:25
AI Öğretmen
Derse devam edelim mi?
06:11:10
Öğrenci
Olur, devam edelim
06:11:12
💭 AI Öğretmen
Tamam, devam edelim
06:11:20
AI Öğretmen
İkizkenar üçgen, üç kenarından ikisi birbirine eşit olan bir üçgen türüdür.
06:11:21
AI Öğretmen
İkizkenar üçgen yapmak için pergel ve ölçüsüz bir cetvel kullanılır.
06:11:22
AI Öğretmen
Pergelin açıklığı değiştirilmeden iki tane aynı büyüklükte çember çizilir.
06:11:25
AI Öğretmen
Bu çemberler çizilirken hem yarıçapları eşit olmalıdır hem de birbirini kesmelidir, yani çemberlerin merkezleri farklı olmalı ve kesişen iki çember olmalıdır.
06:11:27
AI Öğretmen
Daha sonra, bu iki çemberin merkezleri ve çemberlerin yukarıda buluştuğu, yani kesişme noktası cetvelle birleştirilir.
06:11:28
AI Öğretmen
Çemberlerin yarıçapı eşit olduğu için merkezlerden kesişim noktasına giden iki mesafe birbirine eşit olur.
06:11:30
AI Öğretmen
Bu iki eş uzunluk da üçgenin iki kenarını oluşturur.
06:11:31
AI Öğretmen
Sonuçta elde edilen üçgenin iki kenarı eşit olur ve bu da ikizkenar üçgen demektir.
06:11:33
AI Öğretmen
İkizkenar üçgenin nasıl inşa edildiğini anladın mı?

Voltran Okul Analiz Sistemi