← Ana Rapor / DİREN SOYDAN / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
21 October 2025, 16:25
Bitiş
21 October 2025, 16:46
Süre
19 dakika
Durum
Tamamlandı

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Çarpanlar Ve Katlar
Alt Konular:
  • Pozitif Tam Sayıların Pozitif Tam Sayı Çarpanları
Kazanımlar:
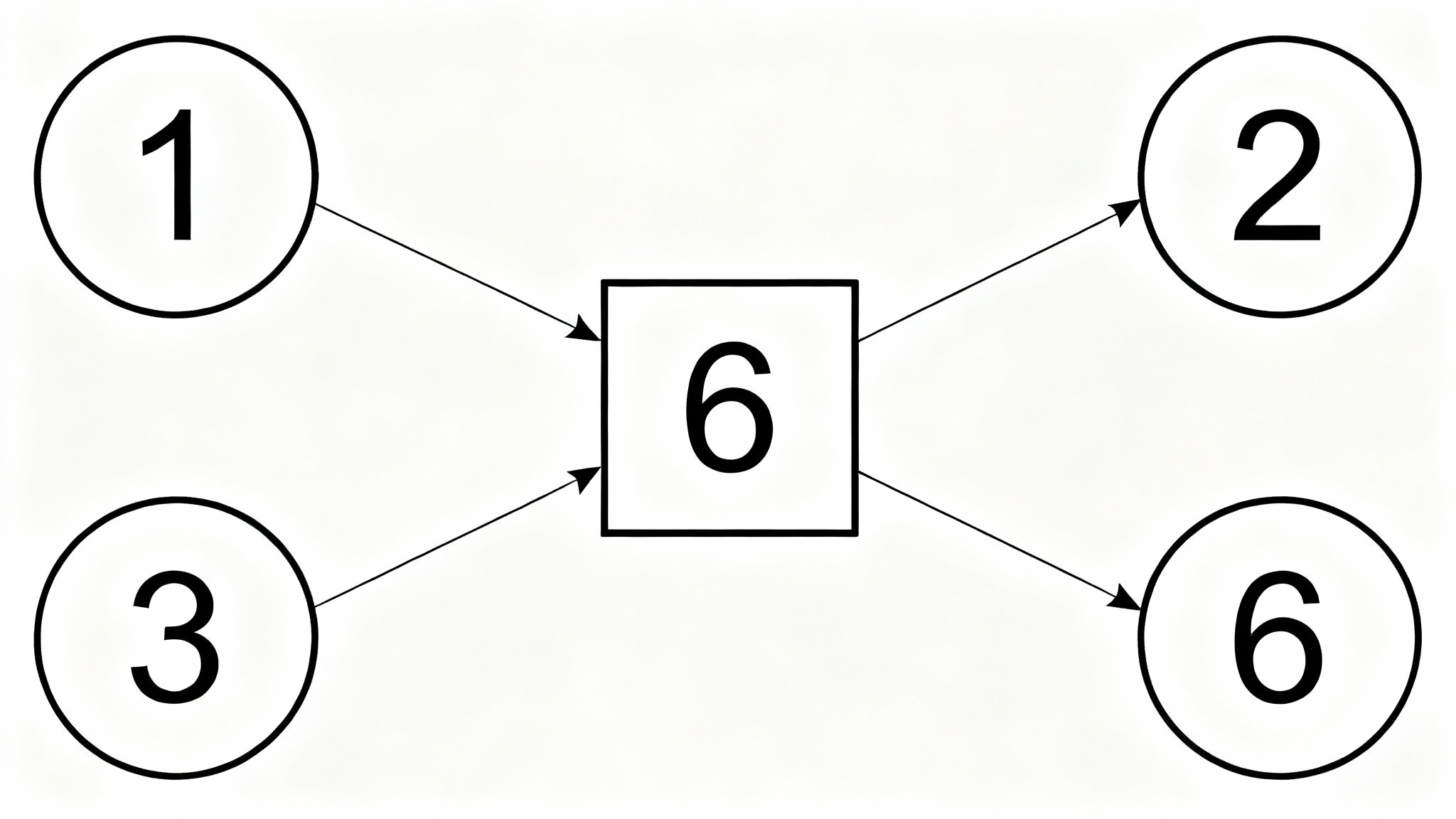
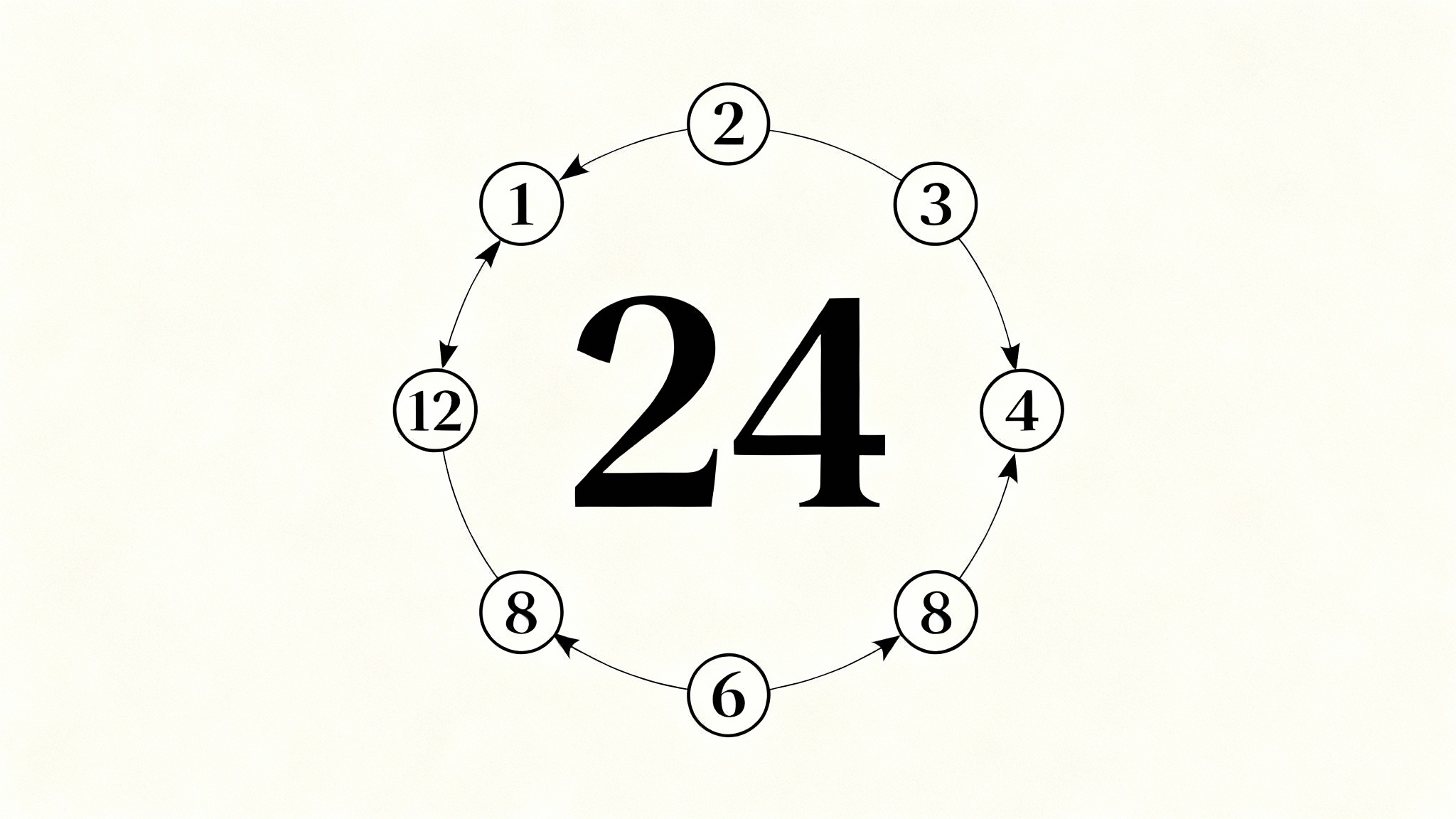
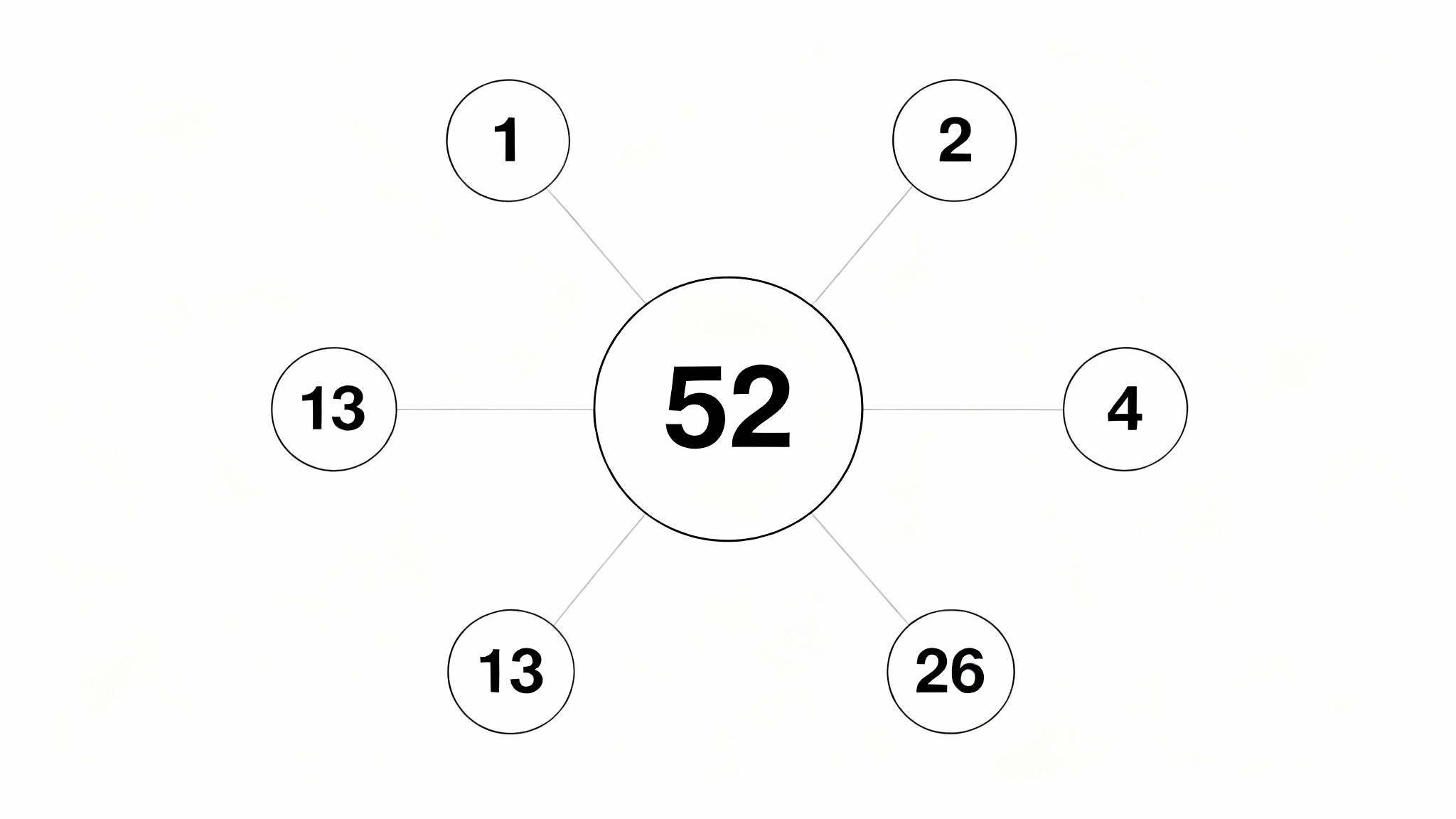
  • Verilen pozitif tam sayıların pozitif tam sayı çarpanlarını bulur, pozitif tam sayıların pozitif tam sayı çarpanlarını üslü ifadelerin çarpımı şeklinde yazar.

Detaylı Değerlendirme

Öğrenci Performans Analizi

Öğrencinin "Çarpanlar ve Katlar" konusundaki performansı değişkenlik göstermektedir. Konunun temel mantığını anladığını belirtse de, problem çözme ve uygulama aşamalarında belirgin eksiklikleri bulunmaktadır.

Genel Değerlendirme:
- Öğrenci, bir sayının pozitif tam sayı çarpanlarını bulma mantığını temel düzeyde kavramıştır. Ancak, bu bilgiyi karmaşık veya çok adımlı problemlere uygulamakta zorlanmaktadır.
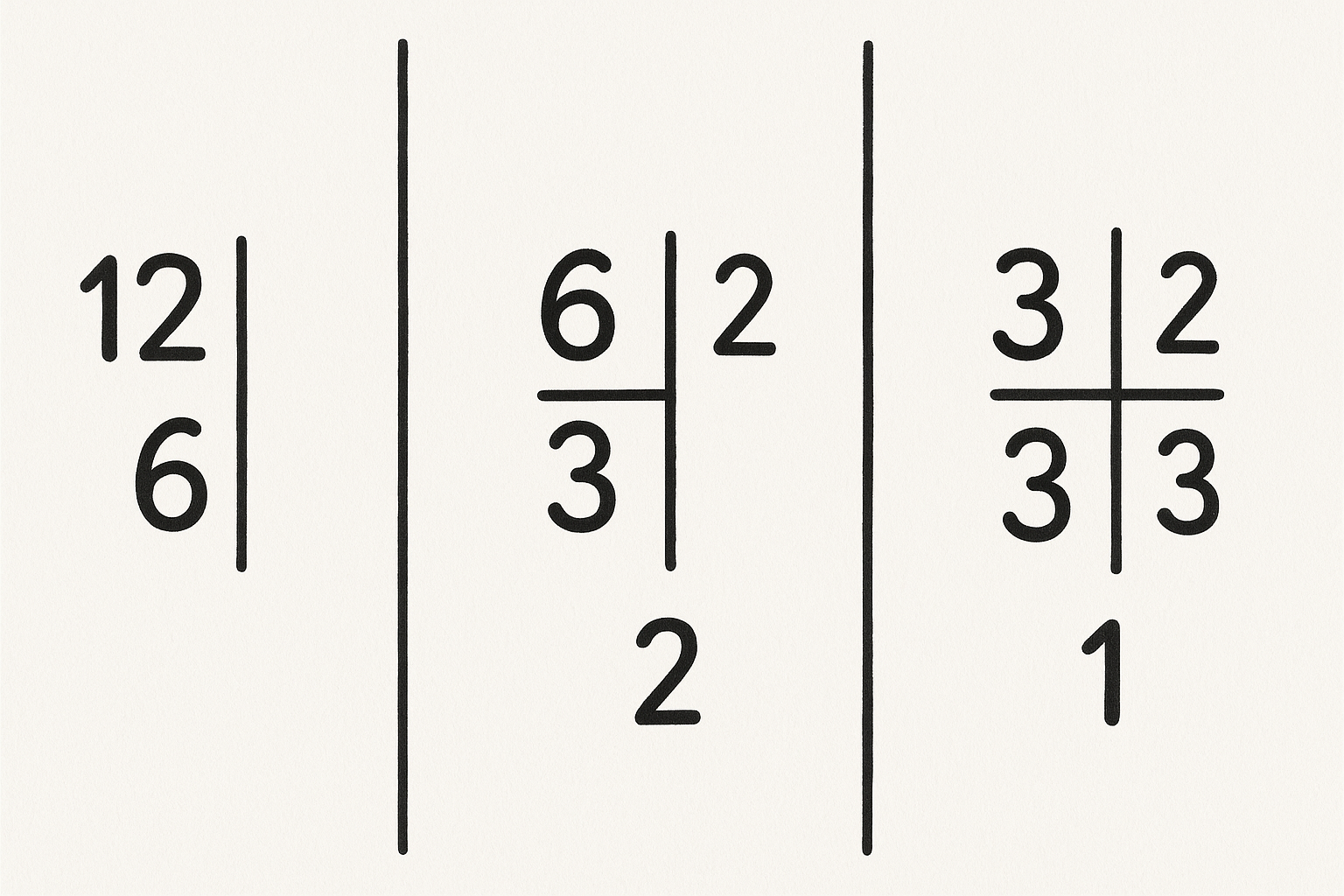
- Dersin başındaki, pozitif tam sayı çarpanlarının sayısını bulmaya yönelik soruyu ("bilmiyorum" diyerek) yanıtsız bırakması, asal çarpanlara ayırma ve üsleri kullanarak çarpan sayısı bulma formülünü bilmediğini veya hatırlamadığını göstermektedir.
- Dikdörtgenin alanından çevresini bulma ile ilgili ikinci soruda, 72'nin tüm çarpan çiftlerini bulamayarak hatalı bir sonuca ulaşmıştır. Bu durum, çarpanları sistematik bir şekilde bulma konusunda pratik eksiği olduğunu göstermektedir.
- Bununla birlikte, dersin sonlarına doğru sorulan ve alanı 144 cm² olan dikdörtgenin en büyük ve en küçük çevre değerleriyle ilgili problemi doğru çözmesi, konsepti anladığında uygulayabildiğini göstermektedir. Bu sorudaki başarısı olumlu bir işarettir.
- "Karekök sınırı neden çarpan bulmada önemli?" gibi bir soru sorması, konuyu ezberlemek yerine mantığını anlamaya çalıştığını gösteren olumlu bir davranıştır.

Öneri:
Öğrencinin, özellikle bir sayının tüm pozitif çarpanlarını eksiksiz bulma ve pozitif çarpan sayısını asal çarpanların üslerinden faydalanarak hesaplama konularında daha fazla pratik yapması gerekmektedir. Temel bilgiye sahip olsa da, bu bilgiyi problem çözme hızına ve doğruluğuna yansıtmak için alıştırmalara ihtiyacı vardır.

📜 Oturum Detayları

16:27:54
Öğrenci
Evet, hazırım Hocam! Bu konuyu detaylıca anlatır mısın?
16:27:54
💭 AI Öğretmen
Tabii, hemen başlıyorum
16:27:54
Görsel
Görsel
16:27:55
AI Öğretmen
Her doğal sayı, iki doğal sayının çarpımı şeklinde yazılabilir.
16:27:55
AI Öğretmen
Bu şekilde çarpılan iki sayıya, ilgili doğal sayının çarpanları denir.
16:27:55
AI Öğretmen
Bir doğal sayının pozitif tam sayı çarpanları, o sayıyı kalansız bölebilen pozitif tam sayılardır.
16:27:55
AI Öğretmen
Yani, pozitif tam sayı çarpanları aynı zamanda o sayının bölenleridir.
16:27:55
AI Öğretmen
Çarpanlar konusu, bir sayının hangi sayılara bölünebildiğini anlamamıza yardımcı olur.
16:27:55
AI Öğretmen
Örnek olarak; 6 sayısının çarpanları 1, 2, 3 ve 6'dır.
16:27:55
AI Öğretmen
Bu sayılar, 6'yı kalansız bölebilen pozitif tam sayılardır.
16:27:55
AI Öğretmen
Pozitif tam sayıların çarpanlarını bulmak, çarpanlar ve katlar konusunun temelini oluşturur.
16:27:55
AI Öğretmen
Anlattığım çarpanlar konusunu anladın mı?
16:28:07
Öğrenci
Anladım
16:28:08
💭 AI Öğretmen
Şimdi pratik yapalım
16:28:08
❓ Soru medium
$A$ pozitif tam sayısının pozitif tam sayı çarpanlarının sayısı $15$'tir. $A \lt 500$ olduğuna göre, $A$'nın alabileceği tüm değerlerin toplamı kaçtır?
16:29:42
Öğrenci
Cevabım: bilmiyorum
16:29:42
💭 AI Öğretmen
Kontrol ediyorum
16:29:43
AI Öğretmen
Cevabın doğru değil, çünkü soruyu çözmek için bazı temel matematiksel bilgileri uygulamak gerekiyor.
16:29:43
AI Öğretmen
Bir sayının pozitif tam sayı çarpanlarının sayısını bulmak için, sayıyı asal çarpanlarına ayırırız. Örneğin, $A = x^a \cdot y^b \cdot z^c \cdot ...$ şeklindeyse, çarpan sayısı $(a+1)(b+1)(c+1)...$ formülü ile hesaplanır.
16:29:43
AI Öğretmen
Soruda çarpan sayısı 15 verilmiş. 15 sayısını çarpanlarına ayırdığımızda, ya tek bir asal sayının kuvveti şeklinde olur ya da iki asal sayının kuvvetlerinin çarpımı şeklinde olur.
16:29:43
AI Öğretmen
İlk durumda, $(a+1) = 15$ yani $a=14$ olur. Örneğin $2^{14} = 16384$ ama bu sayı $500$'den büyük olduğu için kabul etmiyoruz.
16:29:43
AI Öğretmen
İkinci durumda ise, $(a+1)(b+1) = 15$ ve bu çarpanlar 3 ve 5 olabilir. Yani $a=2$ ve $b=4$ ya da tam tersi.
16:29:43
AI Öğretmen
Bu durumda $A = x^4 \cdot y^2$ veya $A = x^2 \cdot y^4$ şeklinde olur. En küçük asal sayılar olan 2, 3 ve 5'i deneyerek $A < 500$ şartını sağlayan sayıları bulabiliriz.
16:29:43
AI Öğretmen
Örnekler: $2^4 \cdot 3^2 = 16 \cdot 9 = 144$, $3^4 \cdot 2^2 = 81 \cdot 4 = 324$, $2^4 \cdot 5^2 = 16 \cdot 25 = 400$ sayıları $500$'den küçüktür ve çarpan sayısı 15'tir.
16:29:43
AI Öğretmen
Bu sayılar dışında $500$'den küçük ve 15 çarpanı olan başka sayı yoktur. Bu sayıların toplamı $144 + 324 + 400 = 868$ olur.
16:29:43
AI Öğretmen
Bu yüzden doğru cevap $868$'dir. Böyle sorularda asal çarpanlara ayırma ve çarpan sayısı formülünü kullanmak çok önemlidir, pratik yapmaya devam etmeni öneririm!
16:29:43
AI Öğretmen
Derse devam edelim mi?
16:32:50
Öğrenci
Olur, devam edelim
16:32:50
💭 AI Öğretmen
Harika, devam edelim
16:32:51
Görsel
Görsel
16:32:51
AI Öğretmen
Bir sayının çarpanları, o sayıyı kalansız bölerek elde edilen pozitif tam sayılardır.
16:32:51
AI Öğretmen
24 sayısının çarpanlarını bulmak için çarpan çiftlerine bakabiliriz: 1 × 24, 2 × 12, 3 × 8 ve 4 × 6.
16:32:51
AI Öğretmen
Bu çarpan çiftlerinden hareketle, 24'ü kalansız bölen pozitif tam sayılar 1, 2, 3, 4, 6, 8, 12 ve 24'tür.
16:32:51
AI Öğretmen
Her bir sayı, başka bir pozitif tam sayı ile çarpıldığında sonucu 24 eder.
16:32:51
AI Öğretmen
Örneğin, 2 × 12 = 24 olduğu için hem 2 hem de 12, 24'ün çarpanlarıdır.
16:32:51
AI Öğretmen
Aynı şekilde, 3 × 8 = 24 ve 4 × 6 = 24 çarpımları da diğer çarpanları gösterir.
16:32:51
AI Öğretmen
Sonuç olarak, 24'ü kalansız bölen pozitif tam sayılar 1, 2, 3, 4, 6, 8, 12 ve 24'tür.
16:32:51
AI Öğretmen
24 sayısının çarpanlarını bulma konusunu anladın mı?
16:33:35
Öğrenci
Anladım
16:33:36
💭 AI Öğretmen
Şimdi bir soru geliyor
16:33:36
❓ Soru medium
Alanı $72$ cm$^2$ olan bir dikdörtgenin kenar uzunlukları, santimetre cinsinden $1$'den büyük birer tam sayıdır. Bu dikdörtgenin çevre uzunluğunun alabileceği kaç farklı tam sayı değeri vardır?
16:34:39
Öğrenci
Cevabım: 4
16:34:40
💭 AI Öğretmen
Kontrol ediyorum
16:34:40
AI Öğretmen
Cevabın doğru değil, çünkü çevre uzunluğunun alabileceği farklı tam sayı değerlerinin sayısını 4 olarak belirtmişsin.
16:34:40
AI Öğretmen
Alanı 72 cm² olan bir dikdörtgenin kenar uzunlukları, 72 sayısının çarpanlarıdır ve 1'den büyük tam sayılar olmalıdır. Bu yüzden 1x72 çifti hariç tutulur. Geriye kalan çiftler: (2,36), (3,24), (4,18), (6,12) ve (8,9).
16:34:40
AI Öğretmen
Her bir kenar çifti için çevre uzunluğu 2(a+b) formülüyle hesaplanır ve bu çevreler sırasıyla 76, 54, 44, 36 ve 34 cm'dir. Bunların hepsi farklı tam sayılardır, bu yüzden çevre uzunluğunun alabileceği farklı tam sayı değeri 5'tir.
16:34:40
AI Öğretmen
Muhtemelen eksik bir kenar çifti veya çevre hesabı yapmamış olabilirsin, bu yüzden cevabın 4 çıktı. Bu tür problemlerde tüm çarpan çiftlerini dikkatlice kontrol etmek önemli.
16:34:40
AI Öğretmen
Özetle, doğru cevap 5 farklı tam sayı değeri vardır: 76, 54, 44, 36 ve 34. Öğrenmeye devam et, böylece benzer sorularda daha dikkatli sonuçlar elde edebilirsin!
16:34:40
AI Öğretmen
Derse devam edelim mi?
16:36:29
Öğrenci
Olur, devam edelim
16:36:29
💭 AI Öğretmen
Hemen ilerliyoruz
16:36:29
Görsel
Görsel
16:36:29
AI Öğretmen
Bir sayının pozitif tam sayı çarpanlarını bulmak için, 1’den başlayıp sayıyı kalansız bölen tüm tam sayılar belirlenir.
16:36:29
AI Öğretmen
Şimdi 52 sayısının çarpanlarını adım adım inceleyelim.
16:36:29
AI Öğretmen
İlk olarak 52'yi 1'e böldüğümüzde 52 elde ederiz, bu yüzden 1 ve 52 çarpandır.
16:36:30
AI Öğretmen
Sonra 52'yi 2'ye böldüğümüzde 26 elde ederiz, yani 2 ve 26 da çarpandır.
16:36:30
AI Öğretmen
52 sayısı 3'e tam bölünmez, bu yüzden 3 çarpan değildir.
16:36:30
AI Öğretmen
52'yi 4'e böldüğümüzde 13 elde ederiz, bu yüzden 4 ve 13 çarpandır.
16:36:30
AI Öğretmen
52 sayısı 5, 6 ve 7'ye tam bölünmez, bu yüzden bu sayılar çarpan değildir.
16:36:30
AI Öğretmen
Başka bir çarpan bulunamadığından, 52'nin tüm pozitif tam sayı çarpanları 1, 2, 4, 13, 26 ve 52'dir.
16:36:30
AI Öğretmen
Pratikte, sadece √52'ye (yaklaşık 7,2) kadar olan sayıları kontrol ederek eşleşen çarpanlar bulunabilir.
16:36:30
AI Öğretmen
52 sayısının pozitif tam sayı çarpanlarını bulma yöntemini anladın mı?
16:38:25
Öğrenci
Karekök sınırı neden çarpan bulmada önemli?
16:38:26
💭 AI Öğretmen
Güzel soru, açıklıyorum
16:38:26
AI Öğretmen
Karekök sınırı, çarpan bulmada önemli çünkü bir sayının çarpanları genellikle kareköküne kadar olan sayılar arasında bulunur.
16:38:26
AI Öğretmen
Örneğin, $52$ sayısında olduğu gibi, $\sqrt{52} \approx 7.2$ olduğundan, sadece 1’den 7’ye kadar olan sayıları kontrol etmek yeterlidir.
16:38:26
AI Öğretmen
Bunun sebebi, eğer $a$ sayısı $n$ sayısının bir çarpanı ise, $n = a \times b$ olur ve $a$ ile $b$ çarpan çifti oluşturur.
16:38:26
AI Öğretmen
Bu durumda, $a$ küçükse $b$ büyüktür ve tam tersi; dolayısıyla her çarpan çifti birisi karekökten küçük, diğeri ise büyük olur.
16:38:26
AI Öğretmen
Bu yüzden karekök sınırı, gereksiz kontrolleri azaltarak işlemi hızlandırır ve kolaylaştırır.
16:38:26
AI Öğretmen
Bu açıklama çarpan bulmadaki karekök sınırını anlamana yardımcı oldu mu?
16:39:01
Öğrenci
Anladım
16:39:02
💭 AI Öğretmen
Şimdi bir soru soracağım
16:39:02
❓ Soru medium
Kenar uzunlukları santimetre cinsinden birer pozitif tam sayı olan bir dikdörtgenin alanı $144 \text{ cm}^2$'dir. Bu bilgilere göre, bu dikdörtgenin çevre uzunluğunun alabileceği en büyük değer ile en küçük değerin farkı kaç santimetredir?
16:40:06
Öğrenci
Cevabım: 242
16:40:06
💭 AI Öğretmen
Kontrol ediyorum
16:40:06
AI Öğretmen
Tebrikler! Cevabın kesinlikle doğru!
16:40:06
AI Öğretmen
Dikdörtgenin alanı sabitken, çevresinin en büyük olması için kenarlarının birbirinden en uzak (1 ve 144), en küçük olması için ise en yakın (12 ve 12) olması gerektiğini çok iyi anlamışsın.
16:40:06
AI Öğretmen
Bu problem, çarpanları kullanarak farklı kenar uzunluklarını bulma ve çevre formülünü doğru uygulama becerini harika bir şekilde gösteriyor.
16:40:06
AI Öğretmen
Bu tür ilişkilendirmeler geometri konularında sana çok yardımcı olacak!
16:40:06
AI Öğretmen
Doğru cevap 242'dir.
16:40:07
AI Öğretmen
Derse devam edelim mi?
16:41:03
Öğrenci
Olur, devam edelim
16:41:03
💭 AI Öğretmen
Harika, devam ediyoruz
16:41:03
Görsel
Görsel
16:41:03
AI Öğretmen
Bir sayının pozitif tam sayı çarpanları arasında, kendisi dışında başka pozitif böleni olmayan asal sayılara o sayının asal çarpanları denir.
16:41:03
AI Öğretmen
Asal çarpanlar, verilen sayıyı tam bölen asal sayılardır.
16:41:04
AI Öğretmen
Bir sayının asal çarpanlarını bulmak için en çok kullanılan yöntemlerden biri bölen listesi yöntemidir.
16:41:04
AI Öğretmen
Bölen listesi yönteminin adımları şu şekildedir:
16:41:04
AI Öğretmen
İlk adımda, asal çarpanlarına ayırmak istediğimiz sayıyı yazar ve yanına dik bir çizgi çekeriz.
16:41:04
AI Öğretmen
İkinci adımda, bu sayıyı kalansız bölen en küçük asal sayıyı çizginin sağına yazar ve bölme işlemini başlatırız.
16:41:04
AI Öğretmen
Üçüncü adımda, elde ettiğimiz sonucu çizginin solundaki sayının altına yazarız.
16:41:04
AI Öğretmen
Dördüncü adımda, sonuç 1 olana kadar aynı işlemi tekrarlayarak her seferinde asal sayılarla böleriz.
16:41:04
AI Öğretmen
Beşinci adımda, çizginin sağına yazdığımız farklı asal sayıları listeleriz.
16:41:04
AI Öğretmen
Örneğin, 12 sayısı için bölen listesi yöntemi şu adımları izler:
16:41:04
AI Öğretmen
12 | 2 → 6
16:41:04
AI Öğretmen
6 | 2 → 3
16:41:04
AI Öğretmen
3 | 3 → 1
16:41:04
AI Öğretmen
Bu işlem sonunda, asal çarpanları 2, 2 ve 3 olur ve 12 = 2·2·3 şeklinde ifade edilir.
16:41:04
AI Öğretmen
Anlattıklarımı anladın mı, yoksa bu konuda soracağın bir şey var mı?
16:42:11
Öğrenci
Anladım
16:42:11
💭 AI Öğretmen
Şimdi soruya geçiyoruz
16:42:12
❓ Soru medium
$A$ ve $B$ pozitif tam sayılarının asal çarpanlarına ayrılmış biçimleri aşağıda verilmiştir: $$ A = 2^x \cdot 3^4 \cdot 5^2 $$ $$ B = 2^3 \cdot 3^y \cdot 7^z $$ Bu sayıların en büyük ortak böleni $\text{EBOB}(A, B) = 2^2 \cdot 3^3$ ve en küçük ortak katı $\text{EKOK}(A, B) = 2^3 \cdot 3^4 \cdot 5^2 \cdot 7^5$ olduğuna göre, $x + y + z$ ifadesinin değeri kaçtır?
16:44:30
Öğrenci
Olur, devam edelim
16:44:30
💭 AI Öğretmen
Hemen devam ediyoruz
16:44:30
AI Öğretmen
Bu derste doğal sayıların çarpanları, pozitif tam sayı çarpanlarının nasıl bulunacağı ve asal çarpanlara ayırma yöntemleri üzerinde durduk. Ayrıca, çarpanların sayıların bölünebilme özelliklerini anlamada nasıl kullanıldığını ve asal çarpanlara ayırma için bölen listesi yöntemini öğrendik. Anladığın ya da sormak istediğin herhangi bir şey var mı?
16:47:02
Öğrenci
Yok.
16:47:02
AI Öğretmen
Bir sonraki derste görüşmek üzere!

Voltran Okul Analiz Sistemi