← Ana Rapor / EKREM KAAN AKHAN / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
10 December 2025, 18:11
Bitiş
Devam ediyor
Süre
29 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Rasyonel Sayılarla İşlemler
Alt Konular:
  • Rasyonel Sayı Problemleri
Kazanımlar:
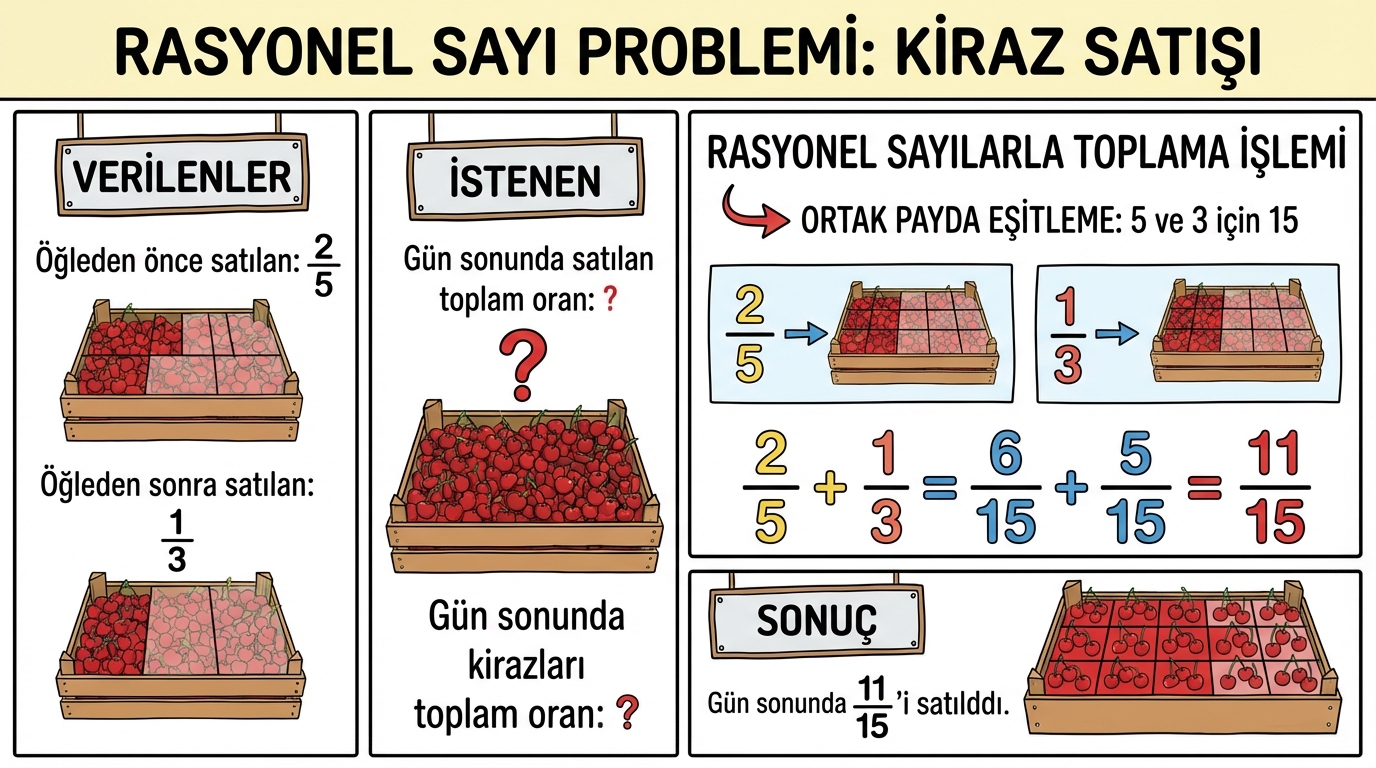
  • Rasyonel sayılarla toplama ve çıkarma işlemlerini yapar.
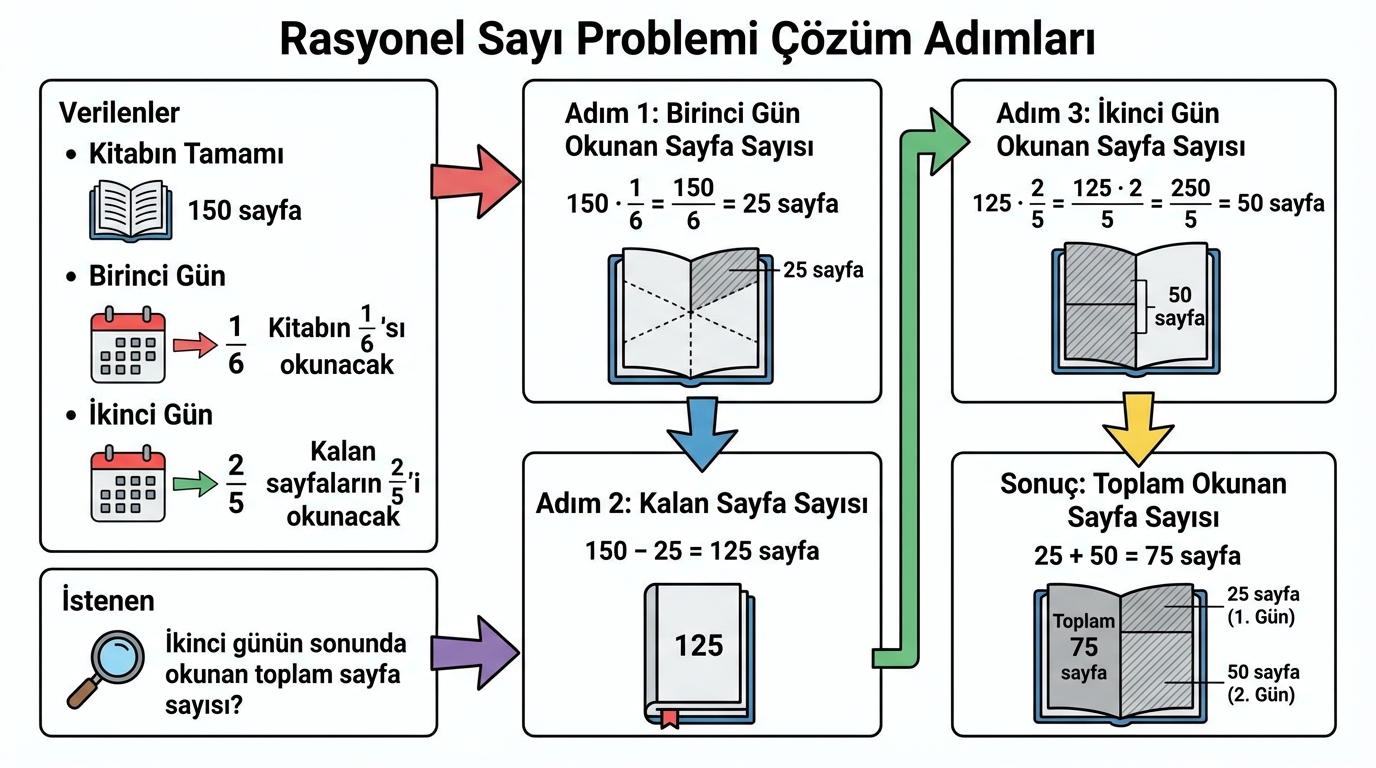
  • Rasyonel sayılarla çok adımlı işlemleri yapar.
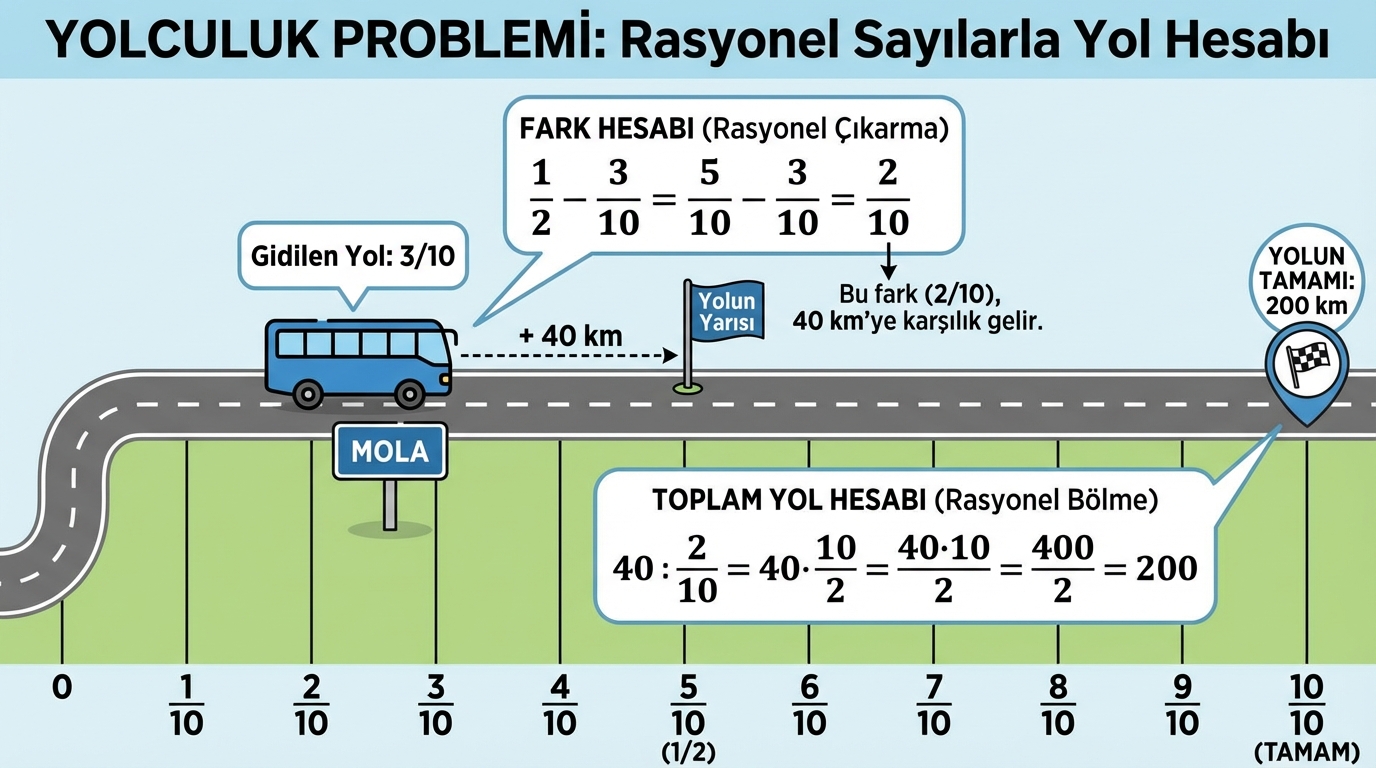
  • Rasyonel sayılarla işlem yapmayı gerektiren problemleri çözer.

Detaylı Değerlendirme

Genel Değerlendirme
Öğrenci, "Rasyonel Sayı Problemleri" konusunda temel zorluklar yaşamaktadır. Dersin başında konuyu anladığını belirtse de, pratik uygulamada önemli hatalar yapmıştır. Özellikle rasyonel sayılarla temel toplama işlemi ve çok adımlı problemlerde eksiklikleri göze çarpmaktadır.

Detaylı Analiz
- Başlangıç: Öğrenci derse konunun detaylıca anlatılmasını isteyerek başlıyor, bu da konuya hazırlıksız olduğunu veya tekrar ihtiyacı duyduğunu gösteriyor.
- Problem Çözme Performansı:
- İlk Soru (Başarılı): Öğrenci, bir problemdeki mantık hatasını ("kalan paranın" ifadesi yerine tüm para üzerinden hesap yapılması) doğru bir şekilde tespit etmiş ve açıklamıştır. Bu, problemdeki kritik noktaları anlama potansiyeli olduğunu göstermektedir.
- İkinci Soru (Başarısız): İki basit rasyonel sayıyı toplama (1/4 + 2/5) sorusunda temel bir hata yapmıştır. Paydaları eşitlemek yerine, işlemi yanlış bir şekilde yaparak `13/5` gibi hatalı bir sonuca ulaşmıştır. Bu, rasyonel sayılarla toplama işleminin temel adımlarında eksikliği olduğunu göstermektedir.
- Üçüncü Soru (Başarısız): "Kalanın kesri" mantığını içeren çok adımlı bir problemi çözmesi istendiğinde (`40` cevabını vermiştir), doğru sonuca (180 TL) ulaşamamıştır. İlk soruda bu tür bir hatayı tespit edebilmesine rağmen, kendisinin bu işlemi yapamaması, teorik bilgiyi pratiğe dökmede zorlandığını göstermektedir.

Sonuç
Öğrencinin rasyonel sayı problemlerini çözebilmesi için öncelikle rasyonel sayılarla temel işlemleri (özellikle toplama ve çıkarma) hatasız yapma becerisini kazanması gerekmektedir. Çok adımlı problemlerde ise "kalanın kesri" gibi ifadelere dikkat etme ve işlem sırasını doğru uygulama konusunda daha fazla pratik yapmaya ihtiyacı vardır.

---

Güçlü Yönler
Bu seansta öğrencinin istikrarlı bir şekilde başarılı olduğu bir konu/kazanım tespit edilememiştir.

Geliştirilmesi Gereken Yönler
Aşağıdaki konularda öğrencinin eksiklikleri tespit edilmiştir:

# Konular:
- Rasyonel Sayılarla İşlemler

# Alt Konular:
- Rasyonel Sayı Problemleri

# Kazanımlar:
- Rasyonel sayılarla toplama ve çıkarma işlemlerini yapar.
- Rasyonel sayılarla çok adımlı işlemleri yapar.
- Rasyonel sayılarla işlem yapmayı gerektiren problemleri çözer.

📜 Oturum Detayları

18:11:46
Öğrenci
Evet, hazırım Hocam! Bu konuyu detaylıca anlatır mısın?
18:11:46
💭 AI Öğretmen
Hemen başlıyorum
18:11:49
AI Öğretmen
Rasyonel sayılarla problemler, kesir ya da ondalık olarak yazılabilen sayıların yani rasyonel sayıların, toplama, çıkarma, çarpma ve bölme işlemlerinin günlük hayattaki durumlara uygulanmasıyla ilgili sorunları içerir.
18:11:50
AI Öğretmen
Bu tip problemleri çözerken, tam sayılarla yapılan problem çözme adımlarını aynen uygularız.
18:11:51
AI Öğretmen
İlk olarak, verilen problemi dikkatlice okuruz.
18:11:53
AI Öğretmen
Daha sonra, bizim için hangi bilgiler verilmiş ve bizden ne isteniyor bunu net bir şekilde belirleriz.
18:11:54
AI Öğretmen
Verilenler, soruyla ilgili bildiğimiz rasyonel sayı bilgilerini, kesirleri, oranları ya da ilişkileri kapsar.
18:11:54
AI Öğretmen
İstenenler ise, bulmamızı isteyen rasyonel sayı veya oranlardır.
18:11:56
AI Öğretmen
Bu adımlardan sonra, problemde verilenler ve istenenler arasındaki ilişkiye göre nasıl bir yol izleyeceğimizi planlarız.
18:11:58
AI Öğretmen
Yani, hangi rasyonel sayıları toplayacağımızı, hangilerini çıkaracağımızı, çarpacağımızı veya böleceğimizi belirleriz.
18:12:01
AI Öğretmen
Son olarak, bu planı adım adım uygularız, işlemleri yaptıktan sonra elde ettiğimiz sonucu problemdeki duruma göre kontrol ederiz.
18:12:01
AI Öğretmen
Rasyonel sayılarla problemleri çözme sürecini anladın mı?
18:13:06
Öğrenci
Anladım
18:13:08
💭 AI Öğretmen
Şimdi bir soru gelecek
18:13:09
❓ Soru medium
Ahmet, başlangıçta sahip olduğu 450 TL'nin 2/5'ini bir kitap almak için harcıyor. Daha sonra, kalan parasının 1/3'ünü bir sinema bileti için kullanıyor. Bu durumu hesaplamaya çalışan bir öğrenci olan Berk, aşağıdaki adımları izliyor: 1. Adım: Kitap için harcanan para: 450 * (2/5) = 180 TL 2. Adım: Sinema bileti için harcanan para: 450 * (1/3) = 150 TL 3. Adım: Toplam harcanan para: 180 + 150 = 330 TL 4. Adım: Kalan para: 450 - 330 = 120 TL Berk'in çözümündeki hata hangi adımda yapılmıştır ve Ahmet'in gerçekte kaç TL'si kalmıştır?
18:16:02
Öğrenci
Cevabım: 2. adımda hata vardır Ferit hocam çünkü kalan paranın değil ilk parasının üçte birini bulmuştur. Gerçekte ise 180 lirası kalmıştır.
18:16:03
💭 AI Öğretmen
Hemen Bakıyorum
18:16:08
AI Öğretmen
Harika bir cevap! Tam isabet!
18:16:09
AI Öğretmen
Berk'in hatasını ve Ahmet'in kalan parasını doğru bir şekilde buldun.
18:16:11
AI Öğretmen
Kesir problemlerinde "kalanın" ifadesine dikkat etmek çok önemli. Önce bir kısmı harcandıktan sonra, ikinci harcamanın kalan miktar üzerinden yapılması gerektiğini çok güzel yakalamışsın.
18:16:12
AI Öğretmen
Bu tür detaylara dikkat etmek, matematik problemlerini doğru çözmenin anahtarıdır. Tebrikler!
18:16:13
AI Öğretmen
Gerçekte ise 180 lirası kalmıştır.
18:16:13
AI Öğretmen
Derse devam edelim mi?
18:16:52
Öğrenci
Olur, devam edelim
18:16:53
💭 AI Öğretmen
Devam ediliyor
18:16:58
Görsel
Görsel
18:17:01
AI Öğretmen
Bir rasyonel sayı problemine başlarken önce soruda verilen bilgilere ve neyin istendiğine dikkatlice bakılır.
18:17:03
AI Öğretmen
Kiraz örneğinde verilen bilgiler, kirazların öğleden önce $\dfrac{2}{5}$'i ve öğleden sonra $\dfrac{1}{3}$'ünün satıldığıdır.
18:17:04
AI Öğretmen
Sorunun bizden istediği ise, bütün gün boyunca toplam satılan kiraz oranını bulmamızdır.
18:17:06
AI Öğretmen
Burada satılan miktarları toplamak için rasyonel sayılarla toplama işlemi yapılır, çünkü her iki zaman diliminde satılan miktarlar ayrı ayrı oranlarla verilmiştir.
18:17:09
AI Öğretmen
Öğleden önce satılan $\dfrac{2}{5}$ ve öğleden sonra satılan $\dfrac{1}{3}$ kesirlerini toplamak gerekir.
18:17:10
AI Öğretmen
Bu iki kesrin paydaları farklı olduğu için önce ortak bir payda bulunur, $5$ ve $3$ için ortak payda $15$'tir.
18:17:12
AI Öğretmen
$\dfrac{2}{5}$ kesrini $15$ paydasına çevirmek için payı ve paydayı $3$ ile çarparız: $\dfrac{2 \times 3}{5 \times 3} = \dfrac{6}{15}$ olur.
18:17:16
AI Öğretmen
Aynı şekilde, $\dfrac{1}{3}$ kesrini $15$ paydasına çevirmek için payı ve paydayı $5$ ile çarparız: $\dfrac{1 \times 5}{3 \times 5} = \dfrac{5}{15}$ olur.
18:17:18
AI Öğretmen
Şimdi bu iki kesri toplayabiliriz: $\dfrac{6}{15} + \dfrac{5}{15} = \dfrac{11}{15}$ elde edilir.
18:17:20
AI Öğretmen
Sonuç olarak, gün sonunda kirazların tamamının $\dfrac{11}{15}$'i satılmıştır.
18:17:20
AI Öğretmen
Bu açıklamayı anladın mı?
18:18:36
Öğrenci
Anladım
18:18:38
💭 AI Öğretmen
Hemen soruya geçiyorum
18:18:39
❓ Soru medium
Bir pastanın önce $\dfrac{1}{4}$'ünü, sonra $\dfrac{2}{5}$'ini yiyen bir kişi hakkında bir arkadaşı, bu kişinin pastanın paylarını toplayarak ($\dfrac{1+2}{4+5} = \dfrac{3}{9}$)'unu, yani sadeleştirerek $\dfrac{1}{3}$'ünü yediğini iddia ediyor. Bu iddiadaki hata nedir ve aslında pastanın toplamda ne kadarı yenmiştir?
18:20:27
Öğrenci
Cevabım: \frac{13}{5}
18:20:28
💭 AI Öğretmen
Hemen Bakıyorum
18:20:32
AI Öğretmen
Cevabınız doğru değil, çünkü kesirlerle toplama yaparken paydaları doğrudan toplamak yanlış olur.
18:20:33
AI Öğretmen
Kesirleri toplarken önce paydaların eşit olması gerekir. Örneğin, \(\frac{1}{4}\) ve \(\frac{2}{5}\) kesirlerinin paydaları farklıdır, bu yüzden en küçük ortak payda bulunur.
18:20:35
AI Öğretmen
Burada 4 ve 5'in en küçük ortak katı 20'dir. Bu yüzden \(\frac{1}{4}\) kesri \(\frac{5}{20}\) ve \(\frac{2}{5}\) kesri \(\frac{8}{20}\) olarak yazılır.
18:20:37
AI Öğretmen
Sonra paylar toplanır: \(5 + 8 = 13\), payda ise 20 olarak kalır. Yani toplam \(\frac{13}{20}\) olur.
18:20:40
AI Öğretmen
Yanlış yapılan şey, payları ve paydaları ayrı ayrı toplamak; bu matematikte doğru değildir. Örneğin \(\frac{1}{2} + \frac{1}{3}\) işlemi \(\frac{1+1}{2+3} = \frac{2}{5}\) değildir, doğru cevap \(\frac{3}{6} + \frac{2}{6} = \frac{5}{6}\)'dır.
18:20:41
AI Öğretmen
Bu yüzden pastanın toplamda \(\frac{13}{20}\)'si yenmiştir, sizin verdiğiniz \(\frac{13}{5}\) cevabı doğru değildir.
18:20:42
AI Öğretmen
Sonuç olarak, doğru cevap \(\frac{13}{20}\) olmalıdır.
18:20:42
AI Öğretmen
Derse devam edelim mi?
18:21:39
Öğrenci
Olur, devam edelim
18:21:40
💭 AI Öğretmen
Devam edelim bakalım
18:21:50
Görsel
Görsel
18:21:52
AI Öğretmen
Bir rasyonel sayı probleminde önce verilenler ve istenen belirlenir.
18:21:53
AI Öğretmen
Bu soruda, kitabın tamamı 150 sayfa olarak verilmiş.
18:21:54
AI Öğretmen
Birinci gün, bu kitabın $\dfrac{1}{6}$'sı okunuyor.
18:21:55
AI Öğretmen
Birinci gün okunan sayfa sayısını bulmak için, 150'nin $\dfrac{1}{6}$'sını hesaplıyoruz:
18:21:57
AI Öğretmen
$$150 \cdot \dfrac{1}{6} = \dfrac{150}{6} = 25 \text{ sayfa}$$
18:21:58
AI Öğretmen
Birinci günün sonunda 25 sayfa okunmuş oluyor.
18:22:00
AI Öğretmen
Kalan sayfa sayısı, 150'den 25 çıkarılarak bulunur:
18:22:02
AI Öğretmen
$150 - 25 = 125$ sayfa kalır.
18:22:04
AI Öğretmen
İkinci gün, bu kalan 125 sayfanın $\dfrac{2}{5}$'i okunuyor.
18:22:05
AI Öğretmen
Bu sefer 125'in $\dfrac{2}{5}$'ini hesaplıyoruz:
18:22:07
AI Öğretmen
$$125 \cdot \dfrac{2}{5} = \dfrac{125 \cdot 2}{5} = \dfrac{250}{5} = 50 \text{ sayfa}$$
18:22:08
AI Öğretmen
İkinci gün 50 sayfa okunmuş olur.
18:22:09
AI Öğretmen
İkinci günün sonunda toplam okunan sayfa sayısı, iki gün okunanların toplamına eşittir.
18:22:11
AI Öğretmen
Toplam okunan sayfa $25 + 50 = 75$ sayfa olur.
18:22:11
AI Öğretmen
Bu kısmı anladın mı?
18:31:29
Öğrenci
Evet, hazırım Hocam! Bu konuyu detaylıca anlatır mısın?
18:31:32
💭 AI Öğretmen
Hemen açıklıyorum
18:31:34
AI Öğretmen
Bu problemde önce kitabın toplam sayfa sayısını ve verilen kesirleri kullanarak her gün kaç sayfa okunduğunu buluyoruz.
18:31:36
AI Öğretmen
Birinci gün kitabın \(\frac{1}{6}\)'sı okunduğunda, toplam 150 sayfanın \(\frac{1}{6}\)'sı olan 25 sayfa okunur.
18:31:38
AI Öğretmen
Birinci günün sonunda kalan sayfa sayısı 150 - 25 = 125'tir. İkinci gün ise kalan sayfaların \(\frac{2}{5}\)'i okunur, bu da 125'in \(\frac{2}{5}\)'i olan 50 sayfadır.
18:31:40
AI Öğretmen
İkinci günün sonunda toplam okunan sayfa sayısı birinci ve ikinci gün okunan sayfaların toplamı, yani 25 + 50 = 75 sayfadır. Anladın mı?
18:32:15
Öğrenci
Anladım
18:32:18
💭 AI Öğretmen
Şimdi bir soru soracağım
18:32:18
❓ Soru medium
Ali, 240 TL parasının önce $\dfrac{1}{4}$'ünü, daha sonra ise kalan parasının $\dfrac{2}{3}$'ünü harcamıştır. Bir öğrenci bu problemi aşağıdaki adımları izleyerek çözmüştür: 1. Adım: İlk harcanan miktar: $240 \cdot \dfrac{1}{4} = 60$ TL 2. Adım: İkinci harcanan miktar: $240 \cdot \dfrac{2}{3} = 160$ TL 3. Adım: Toplam harcanan miktar: $60 + 160 = 220$ TL Bu öğrenci ilk hatayı hangi adımda yapmıştır ve Ali'nin toplam harcadığı miktar gerçekte kaç TL'dir?
18:32:53
Öğrenci
Cevabım: 40
18:32:54
💭 AI Öğretmen
Hemen Bakıyorum
18:33:01
AI Öğretmen
Cevabınız doğru değil, çünkü Ali'nin ikinci harcaması hesaplanırken yanlış bir işlem yapılmış.
18:33:03
AI Öğretmen
İkinci harcama, Ali'nin kalan parasının \(\dfrac{2}{3}\)'ü olarak hesaplanmalı, yani ilk harcamadan sonra kalan para üzerinden işlem yapılmalı.
18:33:06
AI Öğretmen
Adım adım düşünürsek: İlk harcama \(240 \times \dfrac{1}{4} = 60\) TL, kalan para \(240 - 60 = 180\) TL olur.
18:33:08
AI Öğretmen
Sonra ikinci harcama, kalan para üzerinden \(180 \times \dfrac{2}{3} = 120\) TL olarak hesaplanır.
18:33:10
AI Öğretmen
Toplam harcama ise \(60 + 120 = 180\) TL'dir. Öğrenci ikinci adımda kalan para yerine toplam para üzerinden işlem yaparak hata yapmış.
18:33:12
AI Öğretmen
Bu yüzden doğru cevap 180 TL olmalıdır.
18:33:12
AI Öğretmen
Derse devam edelim mi?
18:33:57
Öğrenci
Olur, devam edelim
18:33:58
💭 AI Öğretmen
Devam ediyoruz şimdi
18:34:06
Görsel
Görsel
18:34:10
AI Öğretmen
Bir yolcu otobüsü, gideceği yolun $\dfrac{3}{10}$'unu gittikten sonra mola vermiştir.
18:34:11
AI Öğretmen
Eğer otobüs 40 km daha gitseydi, yolun yarısını yani $\dfrac{1}{2}$'sini tamamlamış olacaktı.
18:34:13
AI Öğretmen
Yolun yarısı ile gidilen kısım arasındaki farkı bulmak için, $\dfrac{1}{2}$ ve $\dfrac{3}{10}$ rasyonel sayılarını birbirinden çıkarıyoruz.
18:34:15
AI Öğretmen
Çıkarma işlemi şöyle yapılır: $\dfrac{1}{2} - \dfrac{3}{10} = \dfrac{5}{10} - \dfrac{3}{10} = \dfrac{2}{10}$
18:34:17
AI Öğretmen
Bu sonuca göre, yolun $\dfrac{2}{10}$'luk kısmı yani beşte biri, 40 km'ye karşılık gelmektedir.
18:34:19
AI Öğretmen
Yolun tamamını bulmak için ise 40 km'yi, bu kısma yani $\dfrac{2}{10}$'a böleriz.
18:34:21
AI Öğretmen
Bir rasyonel sayıya bölme işlemi, bu sayının ters çevrilip çarpılması şeklinde yapılır: $40 : \dfrac{2}{10} = 40 \cdot \dfrac{10}{2}$
18:34:30
AI Öğretmen
Devamında, $40 \cdot \dfrac{10}{2} = \dfrac{400}{2} = 200$ olarak hesaplanır.
18:34:30
AI Öğretmen
Sonuç olarak yolun tamamı 200 km'dir.
18:34:31
AI Öğretmen
Anlattıklarımı bu kısmına kadar anlayabildin mi?
18:36:37
Öğrenci
Evet, hazırım Hocam! Bu konuyu detaylıca anlatır mısın?
18:36:41
💭 AI Öğretmen
Konuya hemen başlıyorum
18:36:45
AI Öğretmen
Bu soruda yolun bir kısmı verilip, yolun tamamı bulunmaya çalışılmıştır. Öncelikle otobüs yolun \(\frac{3}{10}\)'unu gitmiş ve molaya durmuş. Eğer 40 km daha gitseydi, yolun yarısını (\(\frac{1}{2}\)) tamamlamış olacaktı.
18:36:49
AI Öğretmen
Buradan yola devam edersek, yolun yarısı ile şu an gidilen kısmın farkı 40 km'dir. Bu farkı bulmak için \(\frac{1}{2} - \frac{3}{10} = \frac{2}{10}\) bulunmuştur. Yani yolun \(\frac{2}{10}\)'luk kısmı 40 km'ye eşittir.
18:36:53
AI Öğretmen
Yolun tamamını bulmak için 40 km'yi \(\frac{2}{10}\)'a bölüyoruz, bu da \(\frac{40}{\frac{2}{10}} = 40 \times \frac{10}{2} = 200\) km yapar. Böylece yolun tamamı 200 km olarak bulunur. Anladın mı?
18:39:44
Öğrenci
Evet, hazırım Hocam! Bu konuyu detaylıca anlatır mısın?
18:39:48
💭 AI Öğretmen
Hemen açıklıyorum
18:39:52
AI Öğretmen
Tabii, konuyu detaylıca açıklayalım. Otobüs, yolun \(\frac{3}{10}\)'unu gittikten sonra mola vermiş. Eğer 40 km daha gitseydi, yolun yarısına (\(\frac{1}{2}\)) ulaşacaktı.
18:39:55
AI Öğretmen
Burada yolun yarısı ile gidilen kısmın farkı bulunur: \(\frac{1}{2} - \frac{3}{10} = \frac{2}{10}\). Bu fark yolun \(\frac{2}{10}\)'luk kısmına karşılık gelir ve bu kısım 40 km'dir.
18:39:59
AI Öğretmen
Yolun tamamını bulmak için 40 km'yi \(\frac{2}{10}\)'a bölüyoruz; bu da \(40 \times \frac{10}{2} = 200\) km yapar. Böylece yolun tamamı 200 km olarak bulunur. Anladın mı?
18:56:25
Öğrenci
Evet, hazırım Hocam! Bu konuyu detaylıca anlatır mısın?
18:56:27
💭 AI Öğretmen
Hemen açıklıyorum
18:56:30
AI Öğretmen
Bu örnekte yolun bir kısmı gittikten sonra mola veriliyor ve kalan yolun belirli bir mesafesi veriliyor. Öncelikle yolun yarısını ve gidilen kısmını kesirlerle ifade ediyoruz: $\frac{1}{2}$ ve $\frac{3}{10}$.
18:56:34
AI Öğretmen
Ardından bu iki kesir arasındaki farkı buluyoruz: $\frac{1}{2} - \frac{3}{10} = \frac{2}{10}$. Bu fark, 40 km'ye eşit olduğu için, yolun $\frac{2}{10}$'luk kısmı 40 km olarak belirleniyor.
18:56:36
AI Öğretmen
Son olarak, yolun tamamını bulmak için 40 km'yi $\frac{2}{10}$'a bölüyoruz, yani $40 \div \frac{2}{10} = 40 \times \frac{10}{2} = 200$ km yolun tamamı oluyor. Anladın mı?
19:11:59
Öğrenci
Evet, hazırım Hocam! Bu konuyu detaylıca anlatır mısın?
19:12:03
💭 AI Öğretmen
Tabii, hemen başlıyorum
19:12:06
AI Öğretmen
Bu örnekte yolun bir kısmı gittikten sonra kalan mesafe ve yolun yarısı arasındaki fark kullanılarak yolun tamamı bulunuyor. Önce yolun yarısı ile gidilen kısmın farkı hesaplanıyor: \(\frac{1}{2} - \frac{3}{10} = \frac{2}{10}\).
19:12:09
AI Öğretmen
Bu farkın 40 km'ye eşit olduğu bilgisiyle, yolun tamamı 40 km'nin \(\frac{2}{10}\)'a bölünmesiyle bulunuyor: \(40 : \frac{2}{10} = 200\) km. Yani yolun tamamı 200 km'dir.
19:12:10
AI Öğretmen
Anladın mı? Başka bir sorunun var mı?

Voltran Okul Analiz Sistemi