← Ana Rapor / BARTU BAĞCI / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
13 December 2025, 15:35
Bitiş
13 December 2025, 15:43
Süre
7 dakika
Durum
Tamamlandı

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
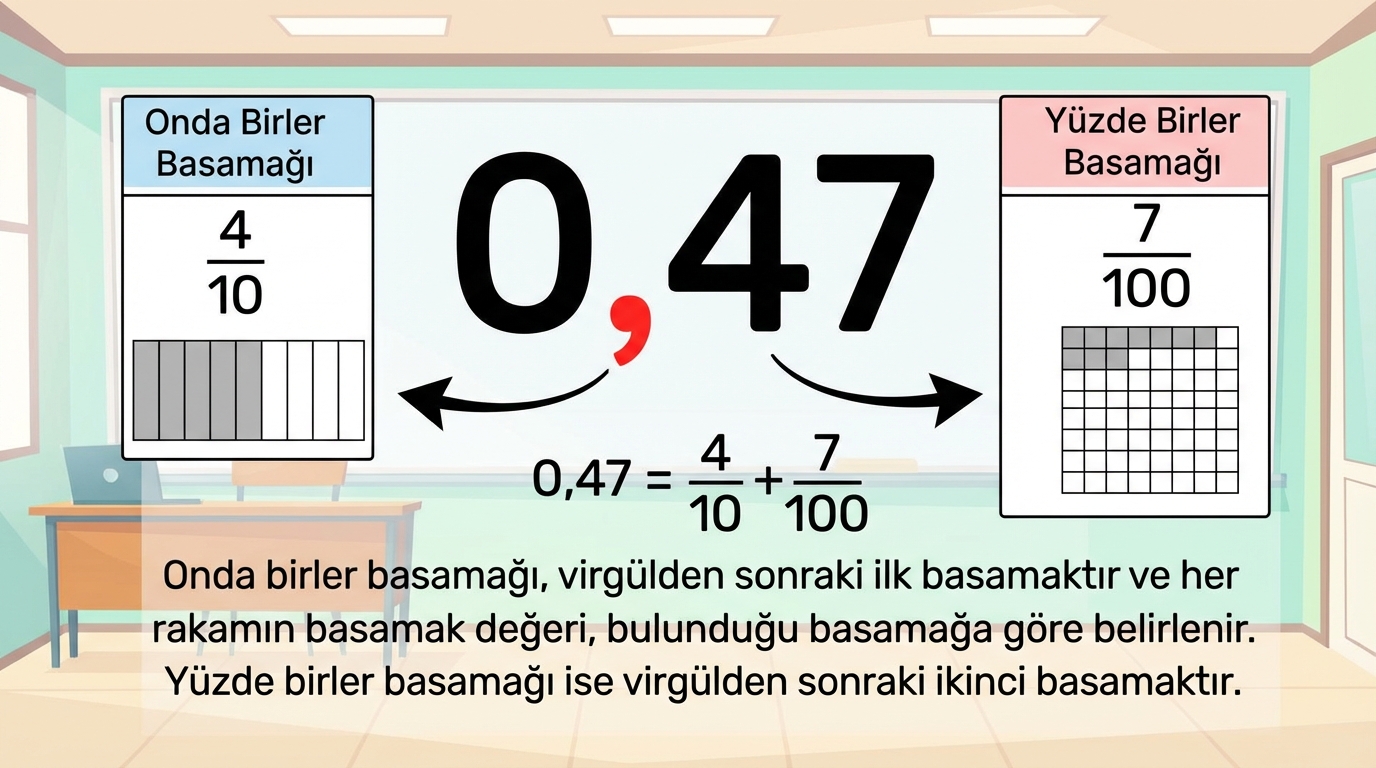
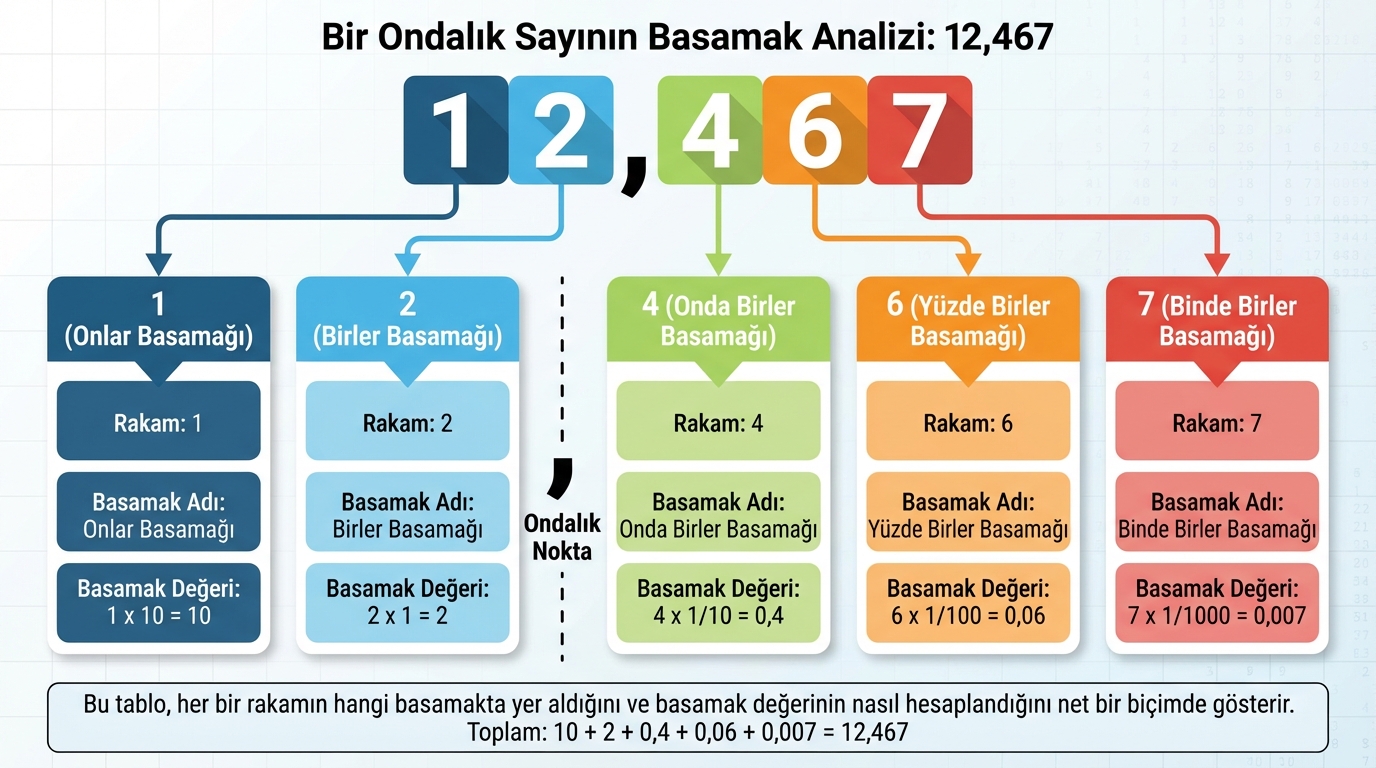
  • Ondalık Gösterimlerde Basamak Değeri
Kazanımlar:
  • Ondalık gösterimleri verilen sayıları çözümler.

Detaylı Değerlendirme

Öğrenci Performans Analizi

Öğrenci, dersin tamamında pasif bir rol oynamıştır. Dersin başında konunun detaylıca anlatılmasını istemiş, ancak anlatım sırasında öğretmenin sorduğu anlama kontrolü sorularına sadece "Anladım" şeklinde cevaplar vermiştir.

Öğrencinin konuyu gerçekten anlayıp anlamadığı, bu cevaplarla ölçülememektedir. Herhangi bir soru sormamış, örnek çözmemiş veya öğretmenin sorduğu bir problemi yanıtlamamıştır. Bu nedenle, öğrencinin aktif katılım göstermemesi ve bilgisini pratikte kullanmaması, konuyu tam olarak kavrayamadığına işaret etmektedir. Anlama seviyesini ölçmek için dersin soru-cevap veya problem çözme aşamasına geçilememiştir.

Sonuç: Öğrencinin teorik anlatımı dinlemiş olmasına rağmen, konuyu anladığına veya uygulayabildiğine dair herhangi bir kanıt bulunmamaktadır. Bu nedenle, tüm konu ve kazanımlarda eksiklikleri olduğu varsayılmalıdır.

📜 Oturum Detayları

15:36:44
Öğrenci
Evet, hazırım Hocam! Bu konuyu detaylıca anlatır mısın?
15:36:46
💭 AI Öğretmen
Harika, başlayalım
15:36:46
Görsel
Görsel
15:36:50
AI Öğretmen
Ondalık gösterim ile kesirler arasındaki ilişki matematikte çok önemlidir.
15:36:51
AI Öğretmen
Geçmişte bazı matematikçiler ve bilim insanları, hesaplamalarda daha hızlı ve doğru sonuçlar almak için ondalık sistemi kullanmışlardır.
15:36:53
AI Öğretmen
Bir kesiri ondalık olarak yazmak, hem hesaplamaları daha hızlı yapmamızı sağlar hem de sonuçlar daha doğru olur.
15:36:54
AI Öğretmen
Ondalık gösterim ve kesirler arasındaki ilişki konusunda anladığınız bir şey var mı?
15:37:25
Öğrenci
Anladım
15:37:30
💭 AI Öğretmen
Güzel, devam edelim
15:37:31
Görsel
Görsel
15:37:33
AI Öğretmen
Ondalık gösterimde **ondalık virgül** kullanımını ilk kez öneren matematikçilerden biri Napier'dir.
15:37:35
AI Öğretmen
Napier'in yaşadığı dönemde, ondalık sayıları göstermek için sayıların arasına virgül koymak alışılmadık ve yeni bir fikirdi.
15:37:36
AI Öğretmen
Napier'in yaptığı çalışmalar sayesinde bu yöntem zamanla daha fazla kabul görmüş ve matematikte yaygın olarak kullanılmaya başlanmıştır.
15:37:38
AI Öğretmen
Bu buluş sayesinde, matematiksel ifadeler daha anlaşılır, daha düzenli ve okunması daha kolay hale gelmiştir.
15:37:39
AI Öğretmen
Türkçede, ondalık ayracı olarak genellikle virgül kullanılır. Örneğin, 0,1 şeklinde yazılır.
15:37:41
AI Öğretmen
Ancak bazı ülkelerde, ondalık ayracı olarak nokta da kullanılabilir.
15:37:42
AI Öğretmen
Ondalık virgülün kullanımını açıklamam yeterince anlaşılır oldu mu?
15:38:19
Öğrenci
Anladım
15:38:21
💭 AI Öğretmen
O zaman devam edelim
15:38:22
Görsel
Görsel
15:38:24
AI Öğretmen
Simon Stevin, ondalık kesirlerin günlük yaşamda daha rahat kullanılabilmesi için yazılma biçimini düzenleyen ilk matematikçilerden biridir.
15:38:26
AI Öğretmen
Stevin, özellikle kesirlerin ondalık sayı şeklinde, yani virgülden sonra gelen sayılarla gösterilmesini önermiştir.
15:38:28
AI Öğretmen
Mesela, $\frac{1}{10}$ ifadesinin 0,1 olarak yazılması gerektiğini söylemiştir.
15:38:29
AI Öğretmen
Bu yaklaşım sayesinde hem matematiksel hesaplamalar hem de günlük hayatta sayılar daha kolay, pratik ve anlaşılır bir şekilde kullanılmaya başlanmıştır.
15:38:30
AI Öğretmen
Anlattıklarımı anladınız mı?
15:39:00
Öğrenci
Anladım
15:39:04
💭 AI Öğretmen
O halde devam edelim
15:39:05
Görsel
Görsel
15:39:07
AI Öğretmen
Bir ondalık gösterimde, virgülden sonraki kısma **ondalık kısmı** denir.
15:39:09
AI Öğretmen
Bu ondalık kısmı, paydası 10, 100 veya 1000 olan kesirlerin toplamı şeklinde yazabiliriz.
15:39:11
AI Öğretmen
Yani, bu tür kesirler ondalık sayıdaki virgülden sonraki basamakların değerlerini gösterir.
15:39:13
AI Öğretmen
Her bir kesir, ondalık kısmın bir basamağının **basamak değerini** belirtir.
15:39:14
AI Öğretmen
Örneğin, virgülden sonraki ilk basamak, onda birler basamağıdır ve $\frac{1}{10}$ olarak yazılır.
15:39:16
AI Öğretmen
İkinci basamak, yüzde birler basamağı olur ve $\frac{1}{100}$ olarak ifade edilir.
15:39:17
AI Öğretmen
Üçüncü basamak ise binde birler basamağıdır ve $\frac{1}{1000}$ şeklinde gösterilir.
15:39:18
AI Öğretmen
Ondalık kısmının kesirlerle nasıl ifade edildiğini anladın mı?
15:39:50
Öğrenci
Anladım
15:39:53
💭 AI Öğretmen
Hadi devam edelim
15:39:53
Görsel
Görsel
15:39:56
AI Öğretmen
0,47 sayısını ondalık gösterimle yazdığımızda, bu sayı $\frac{4}{10} + \frac{7}{100}$ şeklinde ifade edilebilir.
15:39:58
AI Öğretmen
Burada ondalık gösterimdeki 4 rakamı, onda birler basamağında yer alır.
15:39:59
AI Öğretmen
7 rakamı ise yüzde birler basamağında bulunur.
15:40:00
AI Öğretmen
Onda birler basamağı, virgülden sonraki ilk basamak olur.
15:40:02
AI Öğretmen
Her rakamın basamak değeri, o rakamın hangi basamakta olduğuna göre belirlenir.
15:40:03
AI Öğretmen
Yüzde birler basamağı ise virgülden sonraki ikinci basamaktır.
15:40:04
AI Öğretmen
Yani, her basamaktaki rakam farklı bir kesir değeriyle gösterilir ve hangi sayının hangi kesir olduğunu basamağı belirler.
15:40:05
AI Öğretmen
Bu kısmı anladın mı?
15:40:37
Öğrenci
Anladım
15:40:41
💭 AI Öğretmen
Hadi devam edelim
15:40:42
Görsel
Görsel
15:40:45
AI Öğretmen
Ondalık gösterimlerde, bir rakamın hangi basamakta olduğuna göre sahip olduğu değere **basamak değeri** denir.
15:40:47
AI Öğretmen
Basamak değeri, o rakam ile bulunduğu basamağın birim değeri çarpılarak hesaplanır.
15:40:49
AI Öğretmen
Formül olarak, "rakam × basamağın birim değeri" kullanılır.
15:40:50
AI Öğretmen
Örneğin, sayıda 4 rakamı ondalık kısmın ilk basamağındaysa değeri $4 \times 0{,}1 = 0{,}4$ olur.
15:40:52
AI Öğretmen
Her rakam için, o rakamın bulunduğu basamak adı ve konumuna göre bu formül uygulanır.
15:40:52
AI Öğretmen
Bu kısmı anladın mı?
15:41:16
Öğrenci
Anladım
15:41:19
💭 AI Öğretmen
Hadi devam edelim
15:41:19
Görsel
Görsel
15:41:21
AI Öğretmen
Bir ondalık sayıdaki her rakamın bulunduğu yere, yani basamağa göre ayrı bir adı ve bir değeri vardır.
15:41:23
AI Öğretmen
12,467 sayısını incelediğimizde, her rakam bulunduğu basamağın özelliğine göre önem kazanır.
15:41:26
AI Öğretmen
Aşağıdaki tablo, 12,467 sayısındaki her rakamın hangi basamakta olduğunu ve o basamağın değerinin nasıl belirlendiğini açıkça gösterir.
15:41:26
AI Öğretmen
Bu tabloya bakarak, her rakamın basamağını ve basamak değerini kolayca anlayabiliriz.
15:41:27
AI Öğretmen
Buraya kadar anlattıklarımı anladın mı?
15:41:56
Öğrenci
Anladım
15:41:59
💭 AI Öğretmen
Haydi devam edelim
15:42:05
AI Öğretmen
Bu derste ondalık gösterim ile kesirler arasındaki ilişkiyi, ondalık virgül kullanımını ilk öneren Napier'in katkılarını ve Simon Stevin'in ondalık kesirlerin yazılışını standartlaştırmasını öğrendik. Ayrıca ondalık kısmın kesirlerle nasıl ifade edildiğini, basamak değerinin ne olduğunu ve örneklerle nasıl hesaplandığını inceledik. Anlamadığınız veya sormak istediğiniz herhangi bir konu var mı?
15:43:35
Öğrenci
yok çok teşekkürler
15:43:39
AI Öğretmen
Bir sonraki derste görüşmek üzere!

Voltran Okul Analiz Sistemi