← Ana Rapor / ARYA DENİZ ESEOĞLU / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
14 December 2025, 07:44
Bitiş
14 December 2025, 11:50
Süre
42 dakika
Durum
Tamamlandı

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
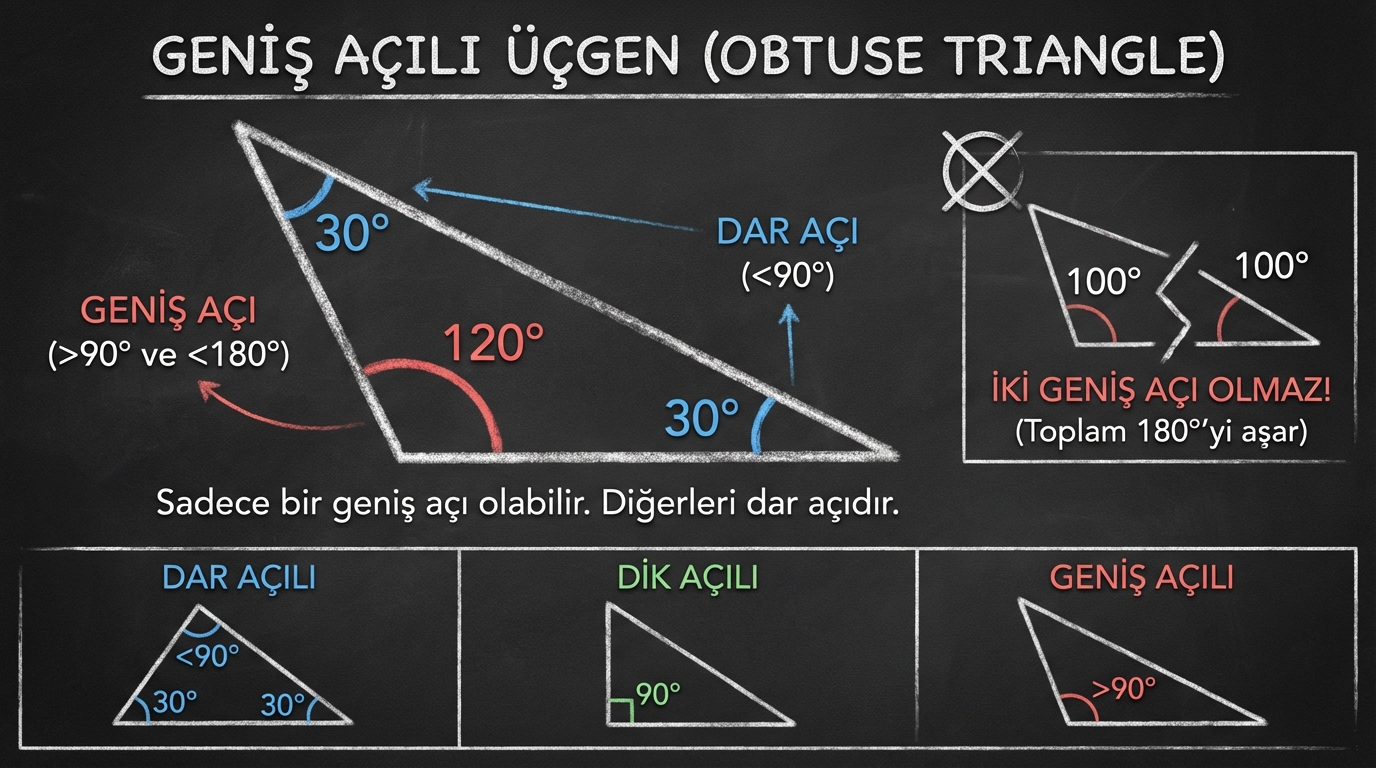
  • Üçgen
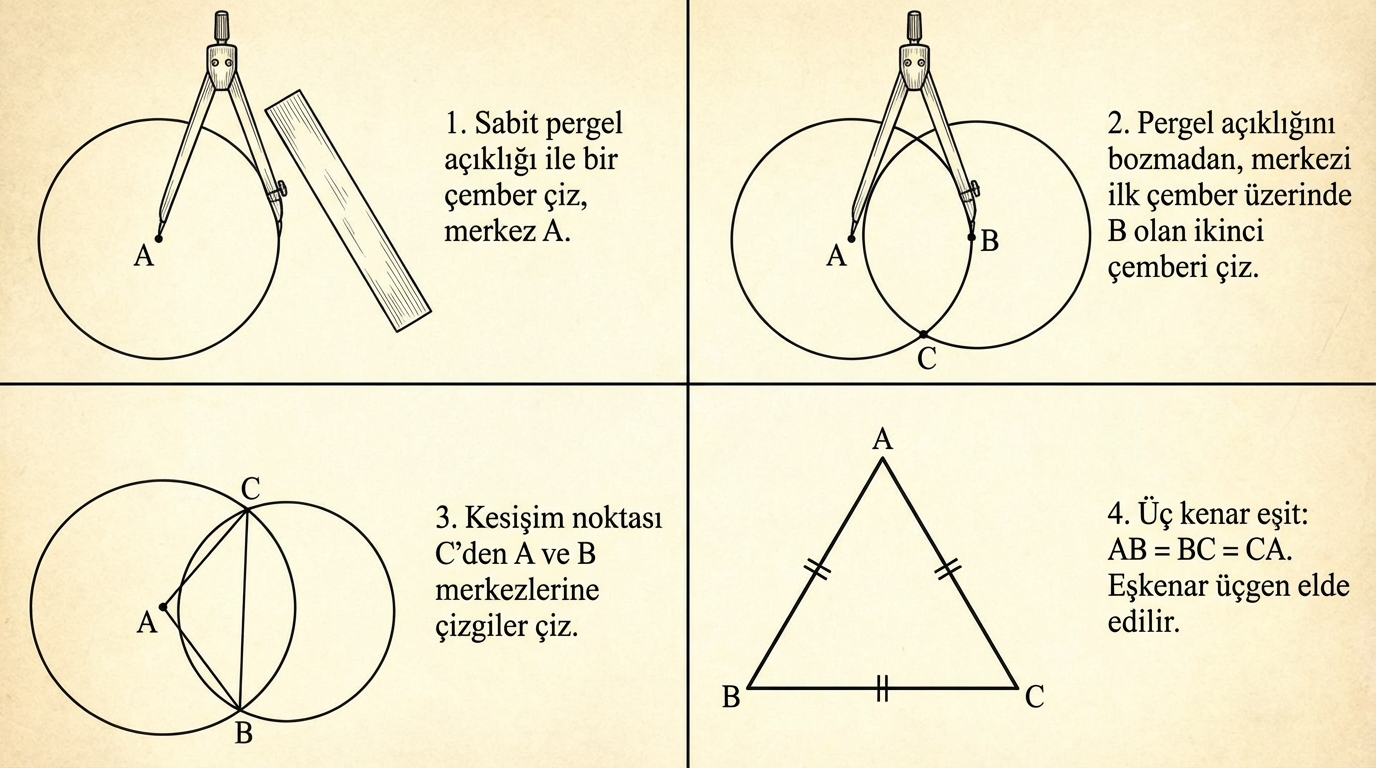
  • Üçgen İnşası
Kazanımlar:
  • Matematiksel araç ve teknoloji yardımıyla düzlemde iki noktada kesişen çember çiftinin merkezleri ve kesişim noktalarından biri ile inşa edilen üçgenlerin kenar özelliklerine yönelik muhakeme yapabilme

Detaylı Değerlendirme

Genel Değerlendirme
Öğrencinin ders boyunca performansı değişkenlik göstermiştir. Temel tanımları ve basit uygulamaları anladığını belirtse de, problem çözme ve muhakeme gerektiren sorularda zorlandığı gözlemlenmiştir. Özellikle, bir problemi çözmek için birden fazla adım gerektiğinde veya temel kuralın dışına çıkan bir durumla karşılaştığında ipucuna ihtiyaç duymaktadır. Geometrik inşa konusunun temel mantığını (örneğin ölçüsüz cetvel kullanımı) kavramakta zorluk çekmiş, ancak dersin sonuna doğru bu konudaki hataları daha iyi tespit etmeye başlamıştır.

İyi Olduğu Konular
Öğrenci, dersin bazı bölümlerinde başarılı olmuştur. Özellikle, bir üçgenin iç açılarının 180 derece olduğu kuralını kullanarak verilmeyen açıyı hesaplama ve üçgenin türünü belirleme gibi temel uygulamalarda başarılı olmuştur. Dersin sonundaki eşkenar üçgen çizimiyle ilgili soruyu da doğru cevaplamıştır. Ancak, genel performansında dalgalanmalar olduğu ve bazı konularda temelden zorlandığı için bu konular "Eksiklikler" listesinde daha detaylı ele alınmıştır.

Eksiklik Gözlemlenen Konular
Öğrencinin aşağıdaki alanlarda desteğe ihtiyacı olduğu tespit edilmiştir:

* Üçgen:
* Problem Çözme: Üçgenin iç açıları toplamının 180° olduğu kuralını bilmesine rağmen, bu bilgiyi cebirsel bir denklem kurmayı gerektiren bir problemde kullanmakta zorlanmış ve iki kez ipucu istemiştir (07:54:45, 07:57:23).
* Kavramsal Hata: Verilen iki açıdan üçüncüsünü doğru hesaplamasına rağmen (70°), cevap olarak "c=180 dir" gibi konudan tamamen kopuk ve anlamsız bir ifade kullanmıştır (08:02:42). Bu durum, temel kavramları birbirine karıştırdığını göstermektedir.

* Üçgen İnşası:
* Temel Prensipler: Geometrik inşanın temel mantığını anlamakta zorlanmıştır. "Ölçüsüz cetvel" kullanımının amacını kavrayamamış ve cetvelin ölçme amacıyla kullanılmasının neden bir hata olduğunu tespit edememiştir (09:56:21).
* Uygulama: İkizkenar üçgen çizimindeki hatayı bulmak için iki kez ipucuna ihtiyaç duymuştur (11:36:16, 11:36:56). Bu, konunun teorik anlatımını anlasa da uygulamada ve problem analizinde zorlandığını göstermektedir.

Tamamen Ders Dışı Sorular/Yorumlar
Ders sırasında öğrencinin tamamen ders dışı bir sorusu veya yorumu olmamıştır.

📜 Oturum Detayları

07:44:24
Öğrenci
Evet, hazırım Hocam! Bu konuyu detaylıca anlatır mısın?
07:44:25
💭 AI Öğretmen
Harika, başlayalım
07:44:26
AI Öğretmen
Üçgen, üç tane kenarı ve üç tane köşesi olan kapalı bir geometrik şekildir.
07:44:28
AI Öğretmen
Üçgenler, köşelerindeki açıların ölçülerine göre sınıflandırılabilir.
07:44:30
AI Öğretmen
Üçgenlerin sınıflandırılmasında, özellikle açıların büyüklüğüne odaklanılır.
07:44:31
AI Öğretmen
Dik açılı üçgen, sadece bir köşesinin ölçüsünün $90°$ olduğu üçgendir.
07:44:33
AI Öğretmen
Üçgendeki bu $90°$’lik açıya dik açı denir.
07:44:34
AI Öğretmen
Bir defterin köşesini düşündüğümüzde, bu köşe $90°$’lik bir dik açıya örnek olabilir.
07:44:35
AI Öğretmen
Eğer bir üçgende bir köşe bu şekildeyse, yani $90°$ ise, o üçgen dik açılı üçgendir.
07:44:37
AI Öğretmen
Bir üçgende iki tane dik açı bulunamaz, çünkü üçgenin iç açılarının toplamı her zaman $180°$’dir.
07:44:39
AI Öğretmen
Eğer iki açı $90°$ olsaydı, $90° + 90° = 180°$ olurdu ve üçüncü açıya yer kalmazdı.
07:44:41
AI Öğretmen
Bu kısmı anladın mı?
07:45:21
Öğrenci
Anladım
07:45:25
💭 AI Öğretmen
Güzel, şimdi devam edelim
07:45:25
❓ Soru medium
Aslı, bir üçgenin iç açılarından ikisinin 90° olabileceğini iddia ediyor ve böyle bir üçgen çizmeye çalışıyor. Aslı'nın bu iddiasının geometrik olarak neden yanlış olduğunu üçgenin iç açıları toplamı kuralını kullanarak açıklayınız. Eğer bir üçgenin iki açısı gerçekten 90° olsaydı, üçüncü açının ölçüsü kaç derece olurdu ve bu durum neden bir üçgen oluşturmazdı?
07:49:40
Öğrenci
Cevabım: üçgen oluşturulamaz çünkü bir üçgenin iç 180 derece dir
07:49:41
💭 AI Öğretmen
Hemen Bakıyorum
07:49:44
AI Öğretmen
Harika bir cevap! Tam isabet!
07:49:45
AI Öğretmen
Bir üçgenin iç açılarının toplamının her zaman 180° olduğunu çok doğru bir şekilde belirttin.
07:49:48
AI Öğretmen
Eğer iki açı 90° olsaydı, bu zaten 180° ederdi ve üçüncü açıya 0° kalırdı ki bu da bir üçgen oluşturmazdı. Açıların toplamı kuralını çok iyi kavramışsın!
07:49:48
AI Öğretmen
Derse devam edelim mi?
07:50:07
Öğrenci
Olur, devam edelim
07:50:08
💭 AI Öğretmen
Güzel, devam edelim
07:50:20
AI Öğretmen
Dar açılı üçgen, üçgenlerin açılarına göre ayrılan çeşitlerinden biridir.
07:50:22
AI Öğretmen
Bir üçgenin dar açılı olabilmesi için, bütün açılarının 90 dereceden küçük olması gerekir.
07:50:23
AI Öğretmen
Bu tür üçgenlerde, üç köşe de sivri ve dardır; hiçbiri 90 dereceye ulaşmaz veya geçmez.
07:50:24
AI Öğretmen
Dar açılı üçgenlerde köşeler sıkışık görünür çünkü geniş açı veya dik açı bulunmaz.
07:50:25
AI Öğretmen
Bir üçgenin yalnızca bir ya da iki açısı dar ise, bu onu otomatik olarak dar açılı üçgen yapmaz.
07:50:26
AI Öğretmen
Dar açılı üçgen olması için, üç açının da dar olması yani 90 dereceden küçük olması zorunludur.
07:50:27
AI Öğretmen
Eğer üçgenin iki açısı dar, bir açısı dik olursa, bu üçgen dar açılı üçgen değil, dik açılı üçgen olur.
07:50:28
AI Öğretmen
Yani, bir üçgenin dar açılı sayılabilmesi için tüm açıların 90 dereceden küçük olması şarttır.
07:50:29
AI Öğretmen
Dar açılı üçgenlerle ilgili anlattıklarımı anladınız mı?
07:51:13
Öğrenci
Anladım
07:51:17
💭 AI Öğretmen
Güzel, devam edelim
07:51:17
❓ Soru medium
Bir üçgenin iç açılarından ikisinin ölçüsü 55° ve 65°'dir. Bu üçgenin açılarına göre türünü belirleyiniz ve nedenini açıklayınız.
07:52:20
Öğrenci
Cevabım: dar açılı üçgendir çünkü açıları 90 dereceden küçüktür
07:52:21
💭 AI Öğretmen
Hemen Bakıyorum
07:52:25
AI Öğretmen
Harika bir cevap!
07:52:27
AI Öğretmen
Üçgenin üçüncü açısını doğru bir şekilde 60° olarak buldun ve tüm açılarının (55°, 65°, 60°) 90°'den küçük olduğunu fark ettin.
07:52:29
AI Öğretmen
Bir üçgenin iç açılarının toplamının 180° olması ve dar açılı üçgenin tüm açılarının 90°'den küçük olması gerektiğini çok iyi anlamışsın.
07:52:29
AI Öğretmen
Bu temel bilgileri kullanarak farklı üçgen türlerini kolayca belirleyebilirsin!
07:52:30
AI Öğretmen
Derse devam edelim mi?
07:52:56
Öğrenci
Olur, devam edelim
07:52:57
💭 AI Öğretmen
Güzel, devam edelim
07:53:04
Görsel
Görsel
07:53:05
AI Öğretmen
Bir üçgenin açılarından biri 90 dereceden büyükse bu üçgene geniş açılı üçgen denir.
07:53:07
AI Öğretmen
Geniş açı, ölçüsü 90 derece ile 180 derece arasında olan açıdır.
07:53:08
AI Öğretmen
Bu yüzden geniş açılı üçgenlerin bir köşesinde yayvan ve diğerlerine göre daha açık görünen bir açı bulunur.
07:53:08
AI Öğretmen
Bir üçgenin iç açılarının toplamı her zaman 180 derecedir.
07:53:11
AI Öğretmen
Bu nedenle, bir üçgende iki geniş açı olamaz; çünkü iki geniş açının toplamı 180 dereceye ulaşır veya aşar ve üçüncü açıya yer kalmaz.
07:53:13
AI Öğretmen
Sonuç olarak geniş açılı üçgenlerde sadece bir geniş açı olabilir, diğer iki açı ise mutlaka dar açı olmalıdır.
07:53:14
AI Öğretmen
Geniş açılı üçgenler, üçgenlerin iç açılarına göre yapılan sınıflandırmada, dar açılı ve dik üçgenlerle birlikte temel üçgen türlerinden birisidir.
07:53:14
AI Öğretmen
Geniş açılı üçgenlerle ilgili bu açıklamayı anladın mı?
07:53:57
Öğrenci
Anladım
07:54:00
💭 AI Öğretmen
Güzel, devam edelim
07:54:00
❓ Soru medium
Bir KLM üçgeni geniş açılı bir üçgendir. Bu üçgenin en büyük açısının ölçüsü 110°'dir. Diğer iki açıdan birinin ölçüsü diğerinin 3 katından 10° fazla olduğuna göre, bu üçgenin en küçük açısı kaç derecedir?
07:54:45
Öğrenci
Bir ipucu verir misiniz hocam?
07:54:46
💭 AI Öğretmen
Bir bakalım
07:54:48
AI Öğretmen
Bir üçgenin iç açılarının toplamının kaç derece olduğunu hatırlıyor musun?
07:54:50
AI Öğretmen
Bu bilgi ışığında, geniş açının 110° olduğu üçgende diğer iki açının toplamı kaç derece olur?
07:54:51
AI Öğretmen
Verilen diğer iki açıdan birinin ölçüsü diğerinin 3 katından 10° fazla olduğuna göre, bu durumu nasıl bir denklemle ifade edebilirsin?
07:57:23
Öğrenci
Bir ipucu verir misiniz hocam?
07:57:25
💭 AI Öğretmen
Hemen düşünüyorum
07:57:28
AI Öğretmen
Merhaba, bir bakalım. Üçgenin iç açılarının toplamı kaç derecedir ve bu bilgi bize neyi söyler?
07:57:29
AI Öğretmen
Geniş açının ölçüsü 110° olduğuna göre, diğer iki açının toplamı kaç derece olur?
07:57:30
AI Öğretmen
Diğer iki açıdan birinin ölçüsünün diğerinin 3 katından 10° fazla olduğu bilgisiyle nasıl bir denklem kurabilirsin?
07:58:48
Öğrenci
Cevabım: 15
07:58:48
💭 AI Öğretmen
Hemen Bakıyorum
07:58:52
AI Öğretmen
Harika bir iş çıkardın! Cevabın kesinlikle doğru!
07:58:54
AI Öğretmen
Bir üçgenin iç açılarının toplamının 180° olduğunu ve verilen bilgileri kullanarak doğru denklemi kurduğunu görmek çok güzel.
07:58:56
AI Öğretmen
Bu problemde hem geometri bilginizi (üçgenin iç açıları toplamı) hem de cebirsel denklemleri çözme becerinizi başarılı bir şekilde kullandınız.
07:58:58
AI Öğretmen
Bu iki önemli matematiksel kavramı birleştirebilmen gerçekten etkileyici!
07:58:59
AI Öğretmen
Dolayısıyla doğru cevap 15'tir.
07:58:59
AI Öğretmen
Derse devam edelim mi?
07:59:46
Öğrenci
Olur, devam edelim
07:59:47
💭 AI Öğretmen
Hemen devam edelim
08:00:00
AI Öğretmen
Her üçgenin iç açıları toplamı her zaman $180^\circ$’dir.
08:00:03
AI Öğretmen
Üçgenin çeşidi fark etmeksizin, yani dar açılı, dik açılı veya geniş açılı olsa da bu kural geçerlidir.
08:00:03
AI Öğretmen
Üçgendeki üç iç açının ölçülerini topladığımızda sonuç her zaman $180^\circ$ olur.
08:00:05
AI Öğretmen
Eğer üçgende iki iç açıyı biliyorsak, bu iki açıyı toplarız ve toplamı $180^\circ$’den çıkarırız.
08:00:06
AI Öğretmen
Böylece kalan değer, üçüncü açının ölçüsüdür.
08:00:07
AI Öğretmen
Bir üçgende bir açı $90^\circ$ ise o üçgen dik üçgendir.
08:00:09
AI Öğretmen
Üçgenin bütün açıları $90^\circ$’den küçükse dar açılı üçgendir.
08:00:11
AI Öğretmen
Üçgenden bir açı $90^\circ$’den büyükse geniş açılı üçgendir.
08:00:12
AI Öğretmen
Bütün bu üçgen türlerinde ortak olan özellik, üç iç açının ölçülerinin toplamının daima $180^\circ$ olmasıdır.
08:00:12
AI Öğretmen
Üçgenlerin iç açılarının toplamıyla ilgili bu kısmı anladınız mı?
08:00:50
Öğrenci
Anladım
08:00:52
💭 AI Öğretmen
Güzel, devam edelim
08:00:53
❓ Soru medium
Bir ABC üçgeninde A açısının ölçüsü 62° ve B açısının ölçüsü 48°'dir. Ali, C açısının ölçüsünü bulmak için şu işlemi yapmıştır: Önce 62 ile 48'i toplayarak 110 bulmuş, sonra da 180'den 110'u çıkararak sonucu 80° olarak hesaplamıştır. Ancak Ali'nin çıkarma işleminde bir hata vardır. Ali'nin hatasını düzelterek C açısının doğru ölçüsünü bulunuz ve bu üçgenin açılarına göre türünü (dar açılı, dik açılı, geniş açılı) belirtiniz.
08:02:42
Öğrenci
Cevabım: 180 den 110nu çıkarırsak cevap 70 olur o zaman c=180 dir
08:02:42
💭 AI Öğretmen
Hemen Bakıyorum
08:02:46
AI Öğretmen
Cevabınız doğru değil, çünkü C açısının ölçüsünü 70° olarak bulduktan sonra "c=180" demeniz yanlış olmuş. Üçgenin bir açısı 180° olamaz.
08:02:49
AI Öğretmen
Üçgenin iç açılarının toplamı her zaman 180°'dir. Siz doğru şekilde 62° ile 48°'i toplayıp 110° buldunuz, sonra 180°'den 110° çıkarınca 70° elde ettiniz. Bu 70° C açısının doğru ölçüsüdür.
08:02:50
AI Öğretmen
Üçgenin açılarına göre türü ise şöyle belirlenir: Eğer tüm açılar 90°'den küçükse üçgen dar açılıdır. Çünkü 62°, 48° ve 70° hepsi 90°'den küçüktür, bu yüzden üçgen dar açılıdır.
08:02:51
AI Öğretmen
Özetle, Ali'nin işlemi doğru, ama sizin "c=180" demeniz yanlış. Doğru cevap C açısının 70° olması ve üçgenin dar açılı olduğudur.
08:02:52
AI Öğretmen
Derse devam edelim mi?
08:03:46
Öğrenci
Olur, devam edelim
08:03:49
💭 AI Öğretmen
Hmm
08:03:58
Görsel
Görsel
08:04:00
AI Öğretmen
Geometrik inşa, sayıların doğrudan kullanılmadığı, yalnızca belirli araçlarla şekillerin oluşturulduğu bir yapma yöntemidir.
08:04:01
AI Öğretmen
Bu yöntemde uzunluklar “5 cm, 7 cm” gibi ölçülerle ifade edilmez, bunun yerine verilen bir uzunluk, açı ya da konum, kullanılan araçlar yardımıyla başka noktalara taşınır veya yeniden üretilir.
08:04:02
AI Öğretmen
Geometrik inşa çalışmalarında temel amaç, verilen şartlara uygun, doğru ve tam bir şekil oluşturmak için yalnızca çizim kurallarına bağlı kalmaktır.
08:04:03
AI Öğretmen
Bu tür inşalarda iki temel araç kullanılır.
08:04:05
AI Öğretmen
Pergel, çember çizmek ve bir noktadan alınan bir uzunluğu başka bir noktaya taşımak için kullanılır; yani bir kez ayarlanan açıklığı sabit tutularak aynı büyüklükte aralıklar tekrar tekrar işaretlenebilir.
08:04:06
AI Öğretmen
Ölçüsüz cetvel ise yalnızca doğru çizmek için kullanılır; üzerindeki sayılara ya da ölçü çizgilerine bakılmaz, sadece iki noktayı birleştiren düz çizgiler çizilir.
08:04:07
AI Öğretmen
Böylece hem pergel hem cetvel birlikte kullanılarak, sayı söylemeden, yalnızca çizim ve çemberlerin özelliklerinden yararlanarak üçgen gibi geometrik şekiller inşa edilir.
08:04:08
AI Öğretmen
Geometrik inşanın temel sırrı, çemberlerin ve doğruların kesişimlerinden yeni noktalar elde ederek istenen üçgenleri oluşturmakta yatar.
08:04:09
AI Öğretmen
Bu kısmı anladın mı yoksa açıklamamı istediğin bir yer var mı?
08:05:24
Öğrenci
Anladım
08:05:27
💭 AI Öğretmen
Güzel, devam edelim
08:05:27
❓ Soru medium
Bir matematik projesinde, Elif'in görevi sadece pergel ve ölçüsüz cetvel kullanarak bir üçgen çizmektir. Elif çizime başlarken ilk olarak cetvelin üzerindeki santimetre işaretlerini kullanarak 8 cm uzunluğunda bir doğru parçası çizer ve bunu üçgenin ilk kenarı olarak belirler. Elif'in bu ilk adımı, metinde anlatılan geometrik inşa kurallarına göre neden hatalıdır ve bu kenarı doğru bir şekilde çizmek için ne yapmalıydı?
09:53:07
Öğrenci
Evet, kaldığımız yerden devam edelim hocam!
09:53:07
💭 AI Öğretmen
Tamam, şimdi en son bu soruya bakıyorduk
09:53:08
❓ Soru medium
Bir matematik projesinde, Elif'in görevi sadece pergel ve ölçüsüz cetvel kullanarak bir üçgen çizmektir. Elif çizime başlarken ilk olarak cetvelin üzerindeki santimetre işaretlerini kullanarak 8 cm uzunluğunda bir doğru parçası çizer ve bunu üçgenin ilk kenarı olarak belirler. Elif'in bu ilk adımı, metinde anlatılan geometrik inşa kurallarına göre neden hatalıdır ve bu kenarı doğru bir şekilde çizmek için ne yapmalıydı?
09:56:21
Öğrenci
Cevabım: ilk önce iki çember çizmelidir sonra bu çemberlerin merkezini bulmalıdır ardından çemberlerin birleştiği en üstte bulunan yere nokta koyup çizgileri birleştimelidir
09:56:22
💭 AI Öğretmen
Hemen Bakıyorum
09:56:26
AI Öğretmen
Cevabınız doğru değil, çünkü soruda Elif’in yaptığı hataya odaklanılması isteniyor. Siz çember çizmekten ve merkez bulmaktan bahsetmişsiniz, ama asıl sorun cetvelin üzerindeki santimetre işaretlerini kullanmasıdır.
09:56:28
AI Öğretmen
Geometrik inşada, ölçüsüz cetvel sadece düz çizgi çizmek için kullanılır, uzunluk ölçmek için değil. Elif cetveldeki santimetre işaretlerini kullanarak 8 cm çizdiğinde, bu kuralı ihlal etmiş oluyor.
09:56:29
AI Öğretmen
Doğru yöntem, pergel kullanarak uzunluğu kopyalamaktır. Pergelin uçlarını başlangıç doğru parçasının uçlarına yerleştirip aralığı sabit tutar, sonra bu aralığı başka bir yere taşıyarak yay çizer. Böylece uzunluk ölçüsüz olarak taşınır.
09:56:31
AI Öğretmen
Özetle, Elif cetveldeki ölçüleri kullanmamalı, sadece pergel yardımıyla uzunluğu kopyalamalıdır. Bu yüzden doğru cevap, ölçüsüz cetveldeki işaretleri kullanmamak ve pergel ile uzunluğu taşımaktır.
09:56:31
AI Öğretmen
Derse devam edelim mi?
09:57:22
Öğrenci
Olur, devam edelim
09:57:24
💭 AI Öğretmen
Hmm
09:57:35
AI Öğretmen
İkizkenar üçgen, iki kenarı birbirine eşit olan üçgen türüdür.
09:57:37
AI Öğretmen
İkizkenar üçgen çizmek için pergel ve ölçüsüz cetvel kullanabiliriz.
09:57:38
AI Öğretmen
Çizime başlarken, pergelin açıklığını değiştirmeden iki eş çember çizeriz.
09:57:39
AI Öğretmen
Bu çemberlerin merkezleri farklı olmalıdır ve yarıçapları aynı olacak şekilde ayarlanır.
09:57:42
AI Öğretmen
Çemberler, birbirini kesecek şekilde konumlandırılır.
09:57:43
AI Öğretmen
Yani, merkezleri farklı, yarıçapları eşit ve birbirini kesen iki çember elde edilir.
09:57:44
AI Öğretmen
Sonra, cetvelle bu iki çemberin merkezleri ile çemberlerin üstte kesiştikleri noktayı birleştiririz.
09:57:44
AI Öğretmen
Bu çizgi ile üçgen oluşur.
09:57:46
AI Öğretmen
Çemberlerin yarıçapları eşit olduğu için, merkezlerden kesişim noktasına kadar olan iki mesafe aynıdır.
09:57:48
AI Öğretmen
Bu uzunluklar, üçgenin iki kenarını oluşturur.
09:57:50
AI Öğretmen
Ortaya çıkan üçgenin iki kenarı eşit olduğu için, bu üçgen bir ikizkenar üçgendir.
09:57:50
AI Öğretmen
İkizkenar üçgenin nasıl inşa edildiğini anladın mı?
09:58:13
Öğrenci
Evet, kaldığımız yerden devam edelim hocam!
09:58:14
💭 AI Öğretmen
En son kaldığımız yeri hızlıca bir tekrar edelim
09:58:15
AI Öğretmen
İkizkenar üçgen, üç kenarından ikisi aynı uzunlukta olan bir üçgen türüdür.
09:58:17
AI Öğretmen
Bu üçgeni çizmek için pergelin açıklığını değiştirmeden iki adet çember çizeriz.
09:58:19
AI Öğretmen
Çemberlerin yarıçapları, yani merkezden kenara olan mesafeleri birbirine eşit olacak şekilde ayarlanır.
09:58:20
AI Öğretmen
Bu iki çemberin merkezlerini farklı yerlere koymamız, yani aralarında mesafe bırakmamız gerekir.
09:58:21
AI Öğretmen
Çemberleri öyle yerleştirmeliyiz ki, ikisi de birbirini bir noktada kessin.
09:58:22
AI Öğretmen
Şimdi cetveli alıp, çemberlerin merkezleriyle çemberin üstte buluştukları noktayı birleştiriyoruz.
09:58:23
AI Öğretmen
Bu şekilde bir üçgen oluşur ve merkezlerden kesişim noktasına giden iki doğru parçası birbirine eşit olur.
09:58:23
AI Öğretmen
Yani üçgenin bu iki kenarı aynı uzunluktadır.
09:58:24
AI Öğretmen
Bu yüzden yaptığımız üçgen ikizkenar üçgen olmuş olur.
09:58:25
AI Öğretmen
İkizkenar üçgenin nasıl inşa edildiği konusunda şimdi daha iyi anladın mı?
09:59:09
Öğrenci
Anladım
09:59:12
💭 AI Öğretmen
Güzel, devam edelim
09:59:12
❓ Soru medium
Ayşe, bir ikizkenar üçgen çizmek için pergel ve cetvel kullanmak istiyor. Önce A merkezli bir çember, daha sonra pergelin açıklığını değiştirerek B merkezli ikinci bir çember çiziyor. Bu iki çemberin kesiştiği noktalardan birini C olarak isimlendiriyor ve A, B ile C noktalarını birleştirerek bir üçgen oluşturuyor. Oluşturduğu ABC üçgeninin [AC] ve [BC] kenar uzunluklarının farklı olduğunu fark ediyor. Ayşe'nin bu çizimde ikizkenar üçgen elde edememesinin sebebi nedir ve doğru sonucu alması için ne yapması gerekirdi?
11:36:04
Öğrenci
Evet, kaldığımız yerden devam edelim hocam!
11:36:05
💭 AI Öğretmen
Tamam, şimdi en son bu soruya bakıyorduk
11:36:05
❓ Soru medium
Ayşe, bir ikizkenar üçgen çizmek için pergel ve cetvel kullanmak istiyor. Önce A merkezli bir çember, daha sonra pergelin açıklığını değiştirerek B merkezli ikinci bir çember çiziyor. Bu iki çemberin kesiştiği noktalardan birini C olarak isimlendiriyor ve A, B ile C noktalarını birleştirerek bir üçgen oluşturuyor. Oluşturduğu ABC üçgeninin [AC] ve [BC] kenar uzunluklarının farklı olduğunu fark ediyor. Ayşe'nin bu çizimde ikizkenar üçgen elde edememesinin sebebi nedir ve doğru sonucu alması için ne yapması gerekirdi?
11:36:16
Öğrenci
Bir ipucu verir misiniz hocam?
11:36:19
💭 AI Öğretmen
Bir bakalım
11:36:20
AI Öğretmen
Ayşe'nin çiziminde hangi adımda pergelin açıklığını değiştirdiğini düşünüyorsun?
11:36:21
AI Öğretmen
İkizkenar üçgenin iki kenarının eşit olması gerektiğini hatırlarsak, bu eşitliği sağlamak için çemberlerin nasıl çizilmesi gerekir?
11:36:22
AI Öğretmen
Çemberlerin yarıçaplarının eşit olması ne anlama gelir ve bu Ayşe'nin çiziminde nasıl bir fark yaratır?
11:36:56
Öğrenci
Bir ipucu verir misiniz hocam?
11:36:58
💭 AI Öğretmen
Bir bakalım şimdi
11:37:00
AI Öğretmen
Ayşe, ikinci çemberi çizerken pergelin açıklığını neden değiştirmiş olabilir?
11:37:01
AI Öğretmen
Çizdiği iki çemberin yarıçapları eşit olsaydı, üçgenin hangi kenarları eşit olurdu?
11:37:02
AI Öğretmen
İkizkenar üçgenin tanımına göre, Ayşe’nin hangi çizim adımını değiştirmesi gerekirdi?
11:38:19
Öğrenci
Cevabım: çemberleri eşit çizmemiş olabilir
11:38:20
💭 AI Öğretmen
Hemen Bakıyorum
11:38:24
AI Öğretmen
Harika bir cevap! Tam da doğru noktayı yakaladın!
11:38:24
AI Öğretmen
Ayşe'nin ikizkenar üçgen elde edememesinin sebebi, çemberleri farklı yarıçaplarla çizmiş olmasıydı.
11:38:25
AI Öğretmen
İkizkenar üçgenin iki kenarının eşit olması gerektiğini hatırlarsak, bu kenarların çemberlerin yarıçapları olduğunu ve bu yarıçapların eşit olması gerektiğini anlarız.
11:38:27
AI Öğretmen
Pergelin açıklığını değiştirmemek, yani aynı yarıçapla çemberler çizmek, ikizkenar üçgen oluşturmak için çok önemli bir adımdır.
11:38:27
AI Öğretmen
Derse devam edelim mi?
11:38:58
Öğrenci
Olur, devam edelim
11:38:59
💭 AI Öğretmen
Tamam, ilerleyelim
11:39:06
Görsel
Görsel
11:39:08
AI Öğretmen
Eşkenar üçgende, bütün kenar uzunlukları birbirine eşittir.
11:39:11
AI Öğretmen
Bir eşkenar üçgeni pergel ve cetvel ile çizerken, pergeli açtığımızda bu açıklığın hiç değişmemesi gerekir.
11:39:12
AI Öğretmen
İlk olarak, pergeli istediğimiz bir açıklığa ayarlarız ve iğnesini herhangi bir noktaya batırarak bir çember çizeriz.
11:39:13
AI Öğretmen
Bu başladığımız noktaya A noktası diyebiliriz, yani bu üçgenin bir köşesi olur.
11:39:15
AI Öğretmen
Pergelin açıklığını bozmadan, iğnesini çemberin çevresi üzerinde başka bir noktaya koyarız ve yine aynı açıklıkla ikinci çemberi çizeriz.
11:39:16
AI Öğretmen
Şimdi ikinci çemberin merkezi, birinci çemberin çizdiğimiz çevresi üzerindedir.
11:39:17
AI Öğretmen
Bu iki çember üstte bir noktada kesişir.
11:39:19
AI Öğretmen
Bu kesişim noktasından, iki merkeze yani A noktasına ve ikincisinin merkezine doğru düz çizgiler çizeriz.
11:39:20
AI Öğretmen
Düz çizgiler sayesinde bir üçgen oluşur.
11:39:21
AI Öğretmen
Çizdiğimiz üçgenin birinci ve ikinci kenarları, çizilen çemberlerin yarıçapları kadardır.
11:39:22
AI Öğretmen
İki merkez arasındaki uzaklık da pergel açıklığından dolayı aynı yarıçap uzunluğundadır.
11:39:23
AI Öğretmen
Böylece üç kenarın hepsi aynı uzunlukta olur ve buna eşkenar üçgen denir.
11:39:24
AI Öğretmen
Bu bölümde anlatılanları anladınız mı?
11:40:14
Öğrenci
Anladım
11:40:21
💭 AI Öğretmen
Hmm
11:40:22
❓ Soru medium
Ayşe, bir eşkenar üçgen çizmek için pergelini 6 cm açarak A merkezli bir çember çiziyor. Daha sonra pergelin iğnesini, bu çember üzerindeki bir B noktasına koyuyor ve pergelin açıklığını yanlışlıkla 5 cm olacak şekilde değiştirerek B merkezli ikinci bir çember çiziyor. Bu iki çemberin kesiştiği C noktasını, A ve B noktalarıyla birleştirerek bir ABC üçgeni oluşturuyor. Ayşe'nin bu çizimde yaptığı hata nedir ve eğer hata yapmasaydı oluşturacağı doğru eşkenar üçgenin çevresi kaç santimetre olurdu?
11:43:14
Öğrenci
Cevabım: pergelin 6cm olmak yerine 5 cm olması eğer hata yapmasaydı üçgenin çevresi 18 cm olurdu
11:43:15
💭 AI Öğretmen
Hemen Bakıyorum
11:43:19
AI Öğretmen
Harika! Çok doğru bir cevap verdin!
11:43:20
AI Öğretmen
Ayşe'nin yaptığı hata, eşkenar üçgen çiziminde pergel açıklığını sabit tutma kuralını ihlal etmesiydi.
11:43:21
AI Öğretmen
Eşkenar üçgenlerin tüm kenarları eşit uzunlukta olmalı ve bu yüzden pergel açıklığı çizim boyunca aynı kalmalıdır.
11:43:22
AI Öğretmen
Eğer hata yapmasaydı, tüm kenarlar 6 cm olacağından üçgenin çevresi 18 cm olurdu.
11:43:23
AI Öğretmen
Bu konuyu çok iyi anlamışsın!
11:43:25
AI Öğretmen
Doğru cevap 18 cm'dir.
11:43:25
AI Öğretmen
Derse devam edelim mi?
11:43:51
Öğrenci
Olur, devam edelim
11:43:53
💭 AI Öğretmen
Hmm
11:44:04
AI Öğretmen
Üçgen çizimlerinde, pergelin açıklığının sabit tutulması çok önemlidir çünkü pergelin ayarı değişirse çizilecek diğer çemberin yarıçapı da değişir.
11:44:07
AI Öğretmen
Eğer ikinci çemberi çizerken pergelin açıklığı kayarsa, iki çemberin yarıçapları birbirine eşit olmaz ve bu da üçgenin kenarlarının eşit çıkmamasına neden olur.
11:44:08
AI Öğretmen
Üçgeni istediğimiz gibi ve doğru özelliklerle çizebilmek için pergelin açıklığı değiştirilmemelidir, aksi halde çizim yanlış olur.
11:44:09
AI Öğretmen
Geometri ile ilgili çizimlerde “ölçüsüz cetvel” ifadesi kullanılır ve bu, cetvel üzerindeki santimetre gibi ölçü işaretlerine bakmadan sadece doğru çizmek için kullanıldığını gösterir.
11:44:12
AI Öğretmen
Yani, cetvel sadece iki nokta arasında düz bir çizgi çizmek için kullanılır, uzunluğun kaç birim olduğu umursanmaz.
11:44:13
AI Öğretmen
Üçgenin köşelerini oluştururken, doğru çizgileri rastgele yerlerden değil, pergelin iğnesinin iziyle oluşan merkez noktalarından ve çemberlerin birbirini kestiği noktalardan geçirmemiz gerekir.
11:44:13
AI Öğretmen
Pergelin açıklığı sabit kaldığında bu merkezlerden ve kesişim noktalarından geçen bütün yaylar ve çemberler aynı yarıçapa sahip olur.
11:44:14
AI Öğretmen
Bu eşit yarıçaplar sayesinde, çizgiler doğru şekilde birleştirilirse, istediğimiz özelliklerde ve doğru ölçülerde üçgenler elde edilir.
11:44:15
AI Öğretmen
Bu açıklamayı anladın mı, yoksa bir kısmını tekrar açıklamamı ister misin?
11:45:56
Öğrenci
Anladım
11:45:59
💭 AI Öğretmen
Güzel, devam edelim
11:45:59
❓ Soru medium
Elif, bir eşkenar üçgen çizmek için pergel ve cetvel kullanıyor. Önce 8 cm uzunluğunda bir AB doğru parçası çiziyor. Sonra pergelini 8 cm açıp sivri ucunu A noktasına koyarak bir yay çiziyor. Bu adımdan sonra, pergelin açıklığını yanlışlıkla 7 cm'e düşürüyor ve sivri ucunu B noktasına koyarak ilk yayı kesen ikinci bir yay çiziyor. Yayların kesişim noktasını C olarak adlandırıp A, B ve C noktalarını birleştiriyor. Elif'in yaptığı hata nedir ve bu hatanın sonucunda ortaya çıkan ABC üçgeni, kenar uzunluklarına göre nasıl bir üçgendir?
11:49:21
Öğrenci
Cevabım: pergelin yanlışlıkla 7 cm ye gelmesi ve böylelikle ikizkenar üçgen oluşturur
11:49:22
💭 AI Öğretmen
Hemen Bakıyorum
11:49:25
AI Öğretmen
Harika bir cevap! Tebrikler!
11:49:26
AI Öğretmen
Elif'in yaptığı hata, eşkenar üçgen çizmek için pergelin açıklığını sabit tutmamasıydı.
11:49:29
AI Öğretmen
Bu hata sonucunda, iki kenarı eşit (8 cm, 8 cm) ve bir kenarı farklı (7 cm) olan bir ikizkenar üçgen oluştu.
11:49:31
AI Öğretmen
Bu, pergelin eşit uzunluktaki kenarları oluşturmadaki rolünü ve ikizkenar üçgenin tanımını çok iyi anladığını gösteriyor!
11:49:31
AI Öğretmen
Derse devam edelim mi?
11:49:55
Öğrenci
Olur, devam edelim
11:49:57
💭 AI Öğretmen
Tamam, devam ediyoruz
11:50:05
AI Öğretmen
Bu derste üçgenlerin açılarına göre sınıflandırılması, dik açılı, dar açılı ve geniş açılı üçgenlerin özellikleri ile geometrik inşa yöntemleri, pergel ve ölçüsüz cetvel kullanarak ikizkenar ve eşkenar üçgenlerin nasıl çizileceği konularını öğrendik. Anlamakta zorlandığınız veya sormak istediğiniz bir şey var mı?
11:50:32
Öğrenci
yok
11:50:37
AI Öğretmen
Bir sonraki derste görüşmek üzere!

Voltran Okul Analiz Sistemi