← Ana Rapor / ÇAĞAN ÇAKIR / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
28 October 2025, 07:20
Bitiş
28 October 2025, 07:41
Süre
22 dakika
Durum
Tamamlandı

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Çarpanlar Ve Katlar
Alt Konular:
  • Pozitif Tam Sayıların Pozitif Tam Sayı Çarpanları
Kazanımlar:
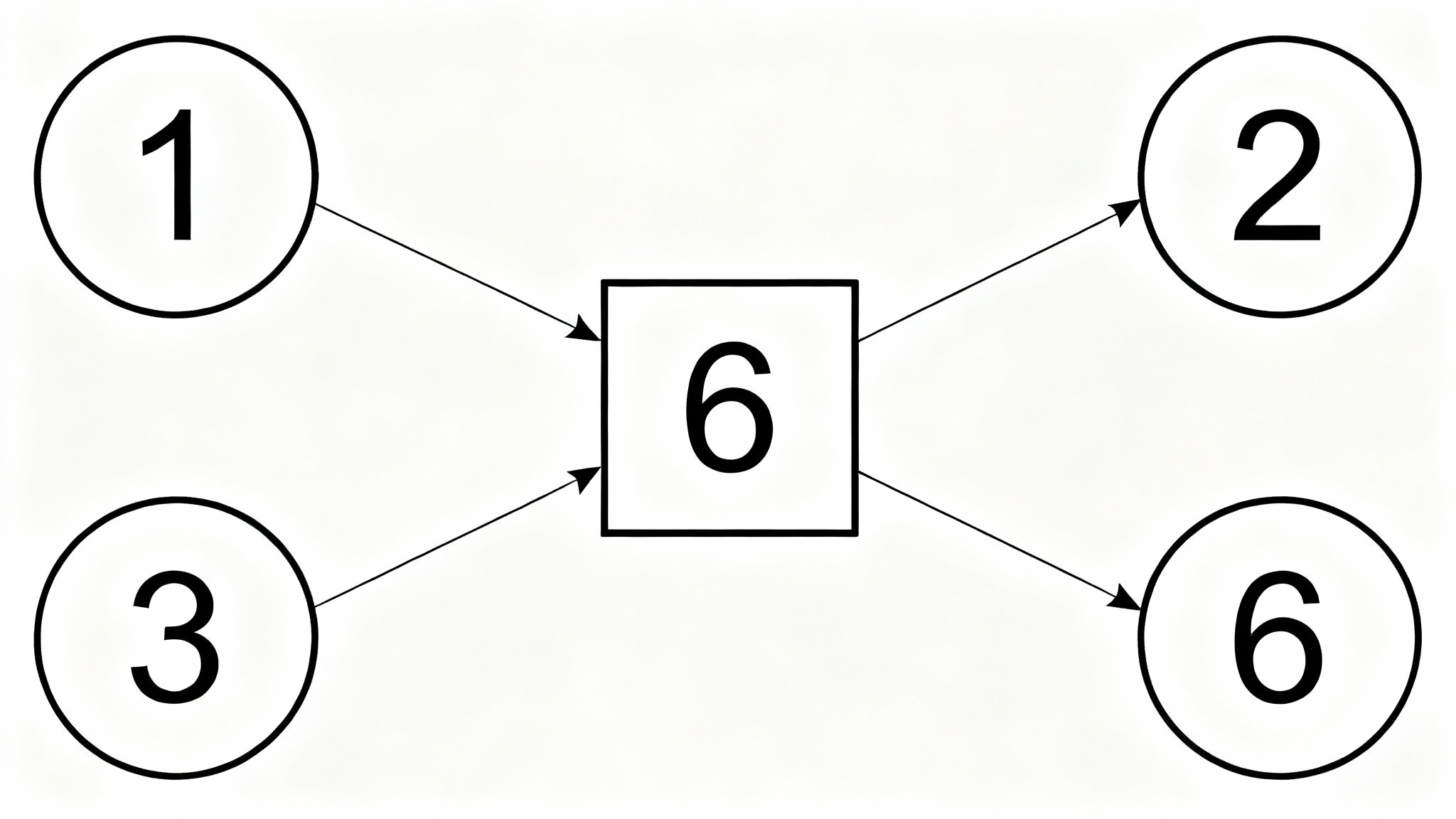
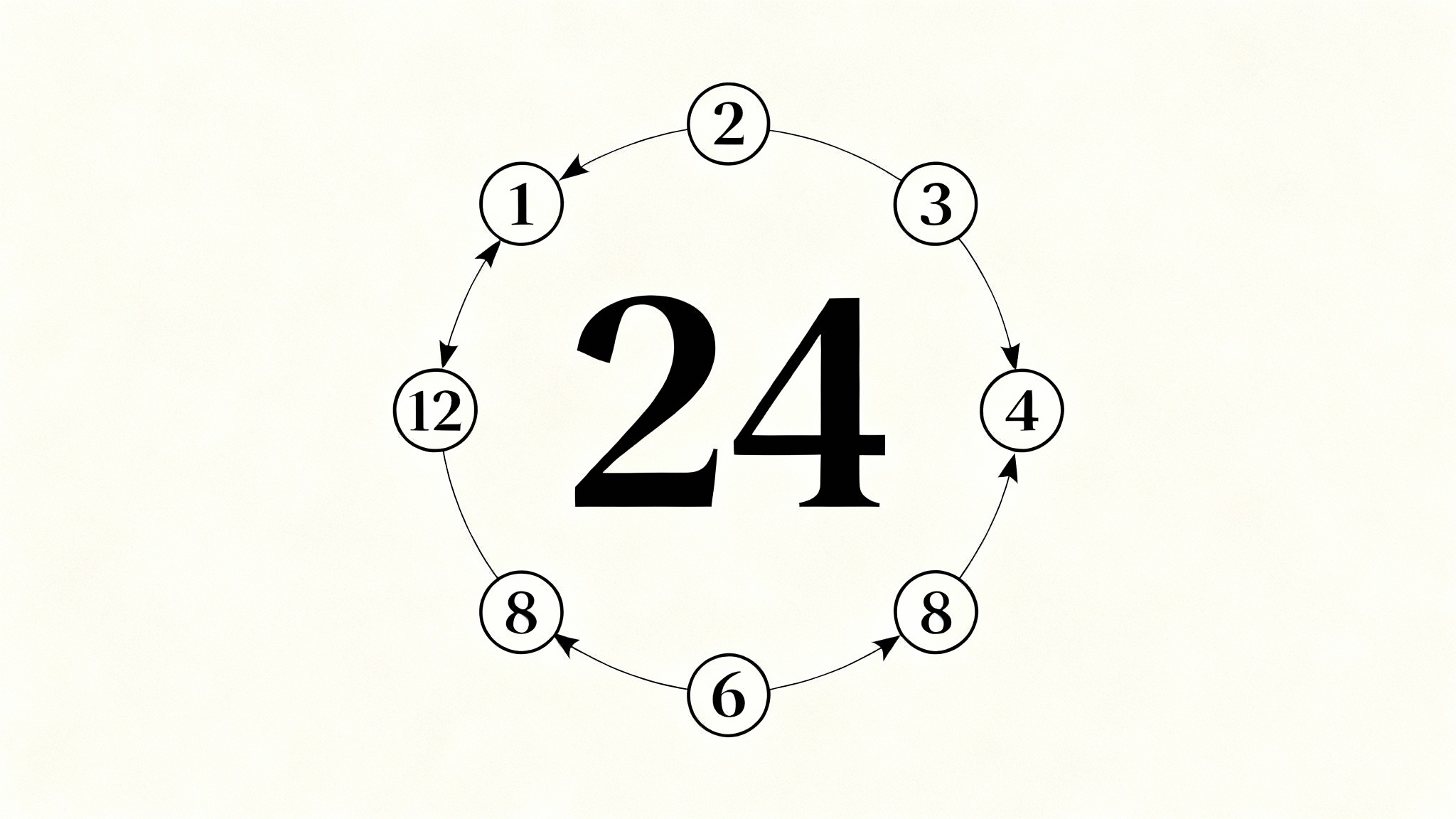
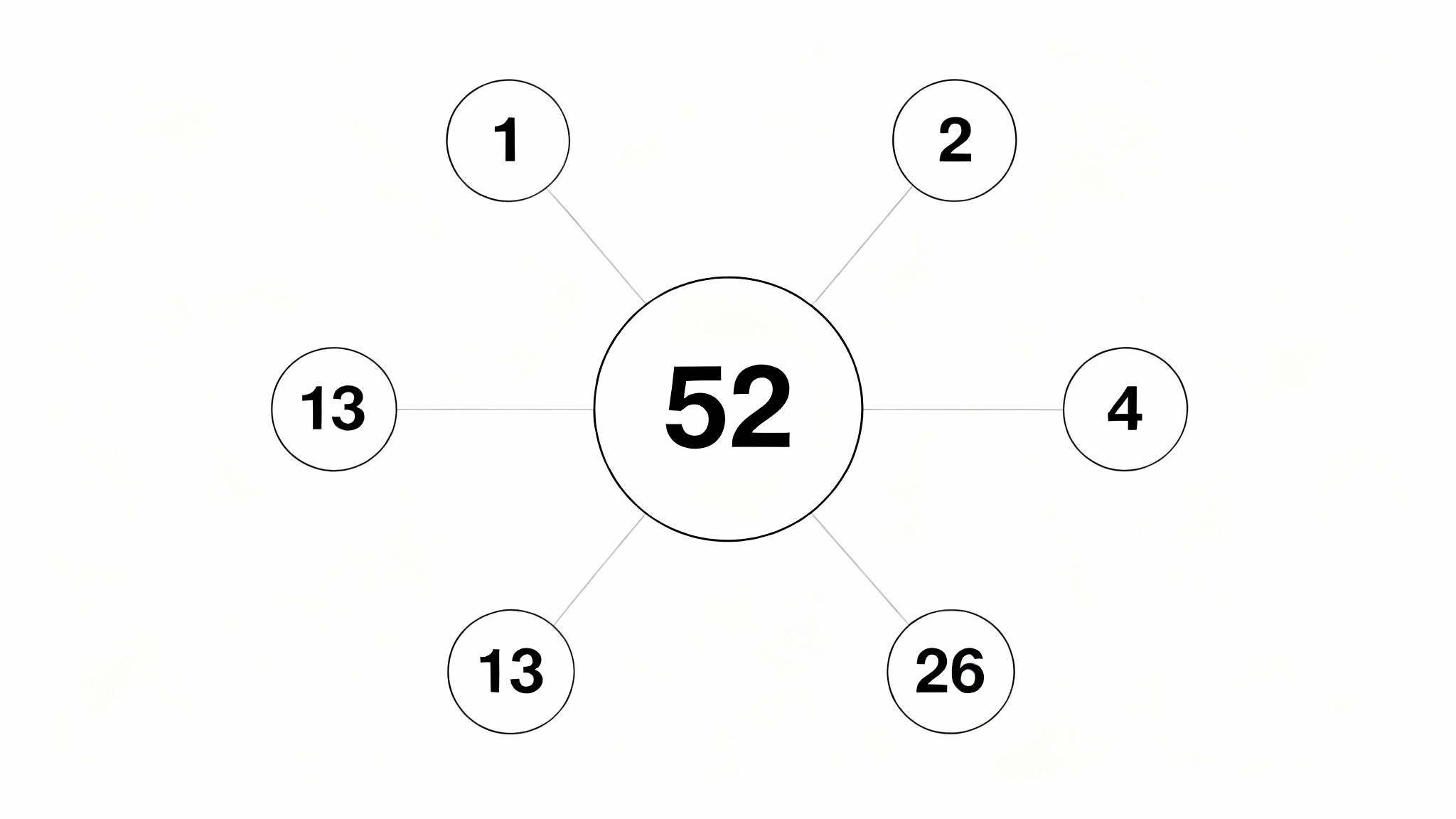
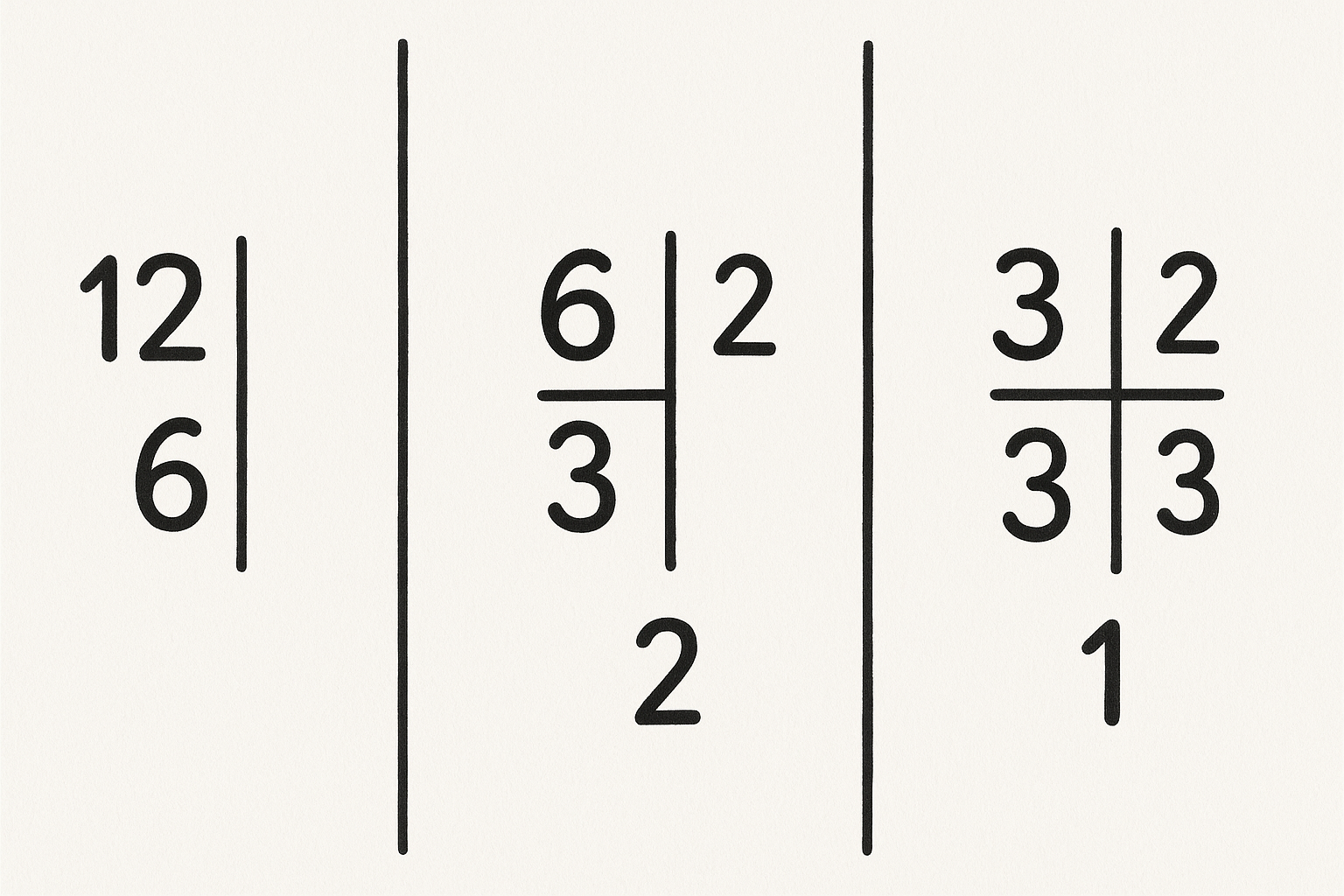
  • Verilen pozitif tam sayıların pozitif tam sayı çarpanlarını bulur, pozitif tam sayıların pozitif tam sayı çarpanlarını üslü ifadelerin çarpımı şeklinde yazar.

Detaylı Değerlendirme

Genel Değerlendirme
Öğrencinin "Çarpanlar ve Katlar" konusunda temel bir anlayışa sahip olduğu ancak bu anlayışı problem çözümüne aktarmada zorluklar yaşadığı gözlemlenmiştir. Özellikle konunun daha karmaşık ve soyut uygulamalarında belirgin eksiklikleri bulunmaktadır. Öğrenci, basit çarpan bulma işlemlerinde başarılı olurken, tüm çarpanları sistematik olarak bulma veya çarpan sayısı formülünü tersten uygulama gibi konularda yardıma ihtiyaç duymuştur.

Öğrencinin Eksiklikleri (Gaps)
Öğrencinin performansında aşağıdaki alanlarda zorluklar tespit edilmiştir:
- Problem Çözme Becerisi: Dersin başındaki ilk soruda, pozitif çarpan sayısı verilen bir sayının alabileceği değerleri bulması istendiğinde, öğrenci iki kez ipucu istemiş ve sonunda "bilemiyorum" yanıtını vermiştir. Bu durum, sayının asal çarpanlarının üsleri ile pozitif çarpan sayısı arasındaki ilişkiyi kuramadığını göstermektedir.
- Sistematik Çarpan Bulma: Alanı 144 cm² olan dikdörtgenin çevre farkı sorusunda yanlış cevap vermiştir. Bu hata, 144 gibi daha çok çarpana sahip bir sayının tüm çarpan çiftlerini eksiksiz bir şekilde bulmakta zorlandığını veya işlem hatası yaptığını düşündürmektedir.
- Konu Derinliği: Konuyu anladığını belirtmesine rağmen, teorik bilgiyi karmaşık problem türlerine uygulamakta zorlanmaktadır.

Öğrencinin İyi Olduğu Konular (Good At)
Öğrenci, bazı temel uygulamalarda başarılı olmuştur:
- Temel Çarpan Bulma: Alanı 72 cm² olan dikdörtgenin olası çevre uzunlukları sorusuna doğru cevap vermiştir. Bu, 72 gibi daha az çarpana sahip bir sayının çarpanlarını doğru bir şekilde bulabildiğini göstermektedir.
- EBOB ve EKOK Bilgisi: Dersin sonlarına doğru sorulan, asal çarpanlarına ayrılmış üslü ifadeler üzerinden EBOB ve EKOK kurallarını kullanarak bilinmeyenleri bulma sorusunu doğru yanıtlamıştır. Bu, EBOB/EKOK konusunun kurallarını anladığını göstermektedir. Ancak bu başarı, "Çarpanlar ve Katlar" konusundaki genel performansının karmaşık olması nedeniyle bu konuyu tamamen anladığı anlamına gelmemektedir.

Ders Dışı Yorumlar
- "etüt bitti mi"
- "sonlandır hocam"

📜 Oturum Detayları

07:20:10
Öğrenci
Evet, hazırım Hocam! Bu konuyu detaylıca anlatır mısın?
07:20:11
💭 AI Öğretmen
Şimdi başlıyoruz
07:20:11
Görsel
Görsel
07:20:13
AI Öğretmen
Her doğal sayı, iki doğal sayının çarpımı olarak yazılabilir.
07:20:14
AI Öğretmen
Bu şekilde çarpılan iki sayıya, o doğal sayının çarpanları denir.
07:20:16
AI Öğretmen
Bir doğal sayının pozitif tam sayı çarpanları, o sayıyı kalansız bölebilen pozitif tam sayılardır.
07:20:17
AI Öğretmen
Başka bir deyişle, pozitif tam sayı çarpanları aynı zamanda o sayının bölenleridir.
07:20:18
AI Öğretmen
Çarpanlar konusu, bir sayının hangi sayılara tam olarak bölünebildiğini anlamamıza yardımcı olur.
07:20:19
AI Öğretmen
Örneğin, 6 sayısının çarpanları 1, 2, 3 ve 6'dır.
07:20:20
AI Öğretmen
Bu sayılar, 6'yı kalansız bölebilen pozitif tam sayılardır.
07:20:21
AI Öğretmen
Pozitif tam sayıların çarpanlarını bulmak, çarpanlar ve katlar konusunun temelini oluşturur.
07:20:22
AI Öğretmen
Anlattıklarımı anladın mı?
07:20:54
Öğrenci
Anladım
07:20:56
💭 AI Öğretmen
Şimdi biraz pekiştirelim
07:20:56
❓ Soru medium
$A$ pozitif tam sayısının pozitif tam sayı çarpanlarının sayısı $15$'tir. $A \lt 500$ olduğuna göre, $A$'nın alabileceği tüm değerlerin toplamı kaçtır?
07:21:28
Öğrenci
Bir ipucu verir misiniz hocam?
07:21:29
💭 AI Öğretmen
Bir bakalım
07:21:31
AI Öğretmen
Çarpan sayısını bulmak için sayının asal çarpanlarına ayrılması gerektiğini biliyor musun?
07:21:32
AI Öğretmen
Asal çarpanların üslerinin toplamından nasıl bir formül çıkarabileceğimizi düşündün mü?
07:21:34
AI Öğretmen
Çarpan sayısı 15 olduğunda, bu sayıyı çarpanlarının sayısını ifade eden çarpanlar olarak nasıl yazabiliriz?
07:22:28
Öğrenci
Bir ipucu verir misiniz hocam?
07:22:29
💭 AI Öğretmen
Bir bakalım
07:22:31
AI Öğretmen
Merhaba, bir bakalım. Pozitif tam sayı çarpanlarının sayısını bulmak için hangi matematiksel yöntemi kullanırız?
07:22:33
AI Öğretmen
Çarpan sayısı 15 olduğunda, bu sayının asal çarpanlarının üsleriyle nasıl bir ilişki kurabiliriz?
07:22:35
AI Öğretmen
15 sayısını çarpanlarının sayısı olarak ifade etmek için hangi asal sayı üslerinin çarpımı şeklinde yazabiliriz?
07:24:03
Öğrenci
Cevabım: bilemiyorum
07:24:03
💭 AI Öğretmen
Hemen Bakıyorum
07:24:07
AI Öğretmen
Cevabınız doğru değil, çünkü soruya henüz bir çözüm getirmediniz; şimdi birlikte doğru çözümü adım adım inceleyelim.
07:24:10
AI Öğretmen
Bir sayının pozitif tam sayı çarpanlarının sayısı, sayının asal çarpanlarının üslerinin birer fazlasının çarpımı ile bulunur. Yani, eğer \(A = x^a \cdot y^b \cdot z^c \cdots\) şeklindeyse, çarpan sayısı \((a+1)(b+1)(c+1) \cdots\) olur.
07:24:12
AI Öğretmen
Soruda, çarpan sayısı 15 olarak verilmiş. 15 sayısını asal çarpanlarına ayırırsak, 15 = 15 ya da 15 = 3 × 5 şeklinde yazabiliriz. Bu iki durumu inceleyeceğiz.
07:24:16
AI Öğretmen
İlk durumda, \(A = x^a\) tek bir asal sayının kuvveti olur ve \((a+1) = 15\) yani \(a=14\) olur. En küçük asal sayı 2 olduğundan, \(A = 2^{14} = 16384\) olur. Ancak 16384 sayısı 500’den büyük olduğu için bu durum sorunun koşulunu sağlamaz.
07:24:19
AI Öğretmen
İkinci durumda, \(A = x^a \cdot y^b\) iki asal sayının kuvvetlerinin çarpımıdır ve \((a+1)(b+1) = 15\) olmalıdır. Burada olası çiftler (3,5) veya (5,3) şeklindedir. Yani ya \(a=2, b=4\) ya da \(a=4, b=2\) olur.
07:24:23
AI Öğretmen
Şimdi \(A < 500\) koşulunu sağlamak için küçük asal sayılarla deneyelim: - \(A = 2^4 \cdot 3^2 = 16 \cdot 9 = 144\) - \(A = 3^4 \cdot 2^2 = 81 \cdot 4 = 324\) - \(A = 2^4 \cdot 5^2 = 16 \cdot 25 = 400\) Bu değerlerin hepsi 500’den küçüktür ve koşulu sağlar.
07:24:25
AI Öğretmen
Daha büyük asal sayılarla denendiğinde sonuçlar 500’den büyük olur, bu yüzden sadece bu üç değer geçerlidir. Bu sayıları toplarsak: 144 + 324 + 400 = 868
07:24:28
AI Öğretmen
Sonuç olarak, \(A\) sayısının alabileceği tüm değerlerin toplamı 868’dir. Bu nedenle doğru cevap 868 olmalıdır.
07:24:30
AI Öğretmen
Bu tür sorularda asal çarpanların üslerini ve çarpan sayısı formülünü iyi kavramak çok önemlidir. Çalışmaya devam ederseniz bu konularda daha başarılı olacaksınız!
07:24:30
AI Öğretmen
Derse devam edelim mi?
07:26:18
Öğrenci
Olur, devam edelim
07:26:18
💭 AI Öğretmen
Devam ediyorum hemen
07:26:27
Görsel
Görsel
07:26:30
AI Öğretmen
Bir sayının çarpanları, o sayıyı tam olarak bölen ve kalan bırakmayan pozitif tam sayılardır.
07:26:31
AI Öğretmen
Örneğin, 24 sayısının çarpanlarını bulmak için farklı sayı çiftlerini çarptığımızda 24 olup olmadıklarına bakarız.
07:26:33
AI Öğretmen
Bu çiftlere bakarsak: 1 × 24, 2 × 12, 3 × 8 ve 4 × 6 gibi çarpmalar elde edebiliriz.
07:26:34
AI Öğretmen
Burada kullanılan her bir sayı, 24'ü kalansız böldüğü için 24'ün bir çarpanıdır.
07:26:36
AI Öğretmen
Yani, 24'ü tam bölen pozitif tam sayılar şunlardır: 1, 2, 3, 4, 6, 8, 12 ve 24.
07:26:38
AI Öğretmen
Bu sayıların her biri, farklı bir pozitif tam sayı ile çarpıldığında sonucu yine 24 yapar.
07:26:40
AI Öğretmen
Örneğin, 2 × 12 = 24 olduğu için hem 2 hem de 12, 24'ün çarpanıdır.
07:26:42
AI Öğretmen
Aynı mantıkla 3 × 8 = 24 ve 4 × 6 = 24 işlemlerinde kullandığımız tüm sayılar da 24'ün çarpanlarıdır.
07:26:44
AI Öğretmen
Sonuç olarak, 24'ü kalansız bölebilen pozitif tam sayılar 1, 2, 3, 4, 6, 8, 12 ve 24'tür.
07:26:45
AI Öğretmen
Bu kısmı anladın mı?
07:27:38
Öğrenci
Anladım
07:27:40
💭 AI Öğretmen
Şimdi bir soru soracağım
07:27:40
❓ Soru medium
Alanı $72$ cm$^2$ olan bir dikdörtgenin kenar uzunlukları, santimetre cinsinden $1$'den büyük birer tam sayıdır. Bu dikdörtgenin çevre uzunluğunun alabileceği kaç farklı tam sayı değeri vardır?
07:30:09
Öğrenci
Cevabım: 5
07:30:09
💭 AI Öğretmen
Hemen Bakıyorum
07:30:14
AI Öğretmen
Harika bir iş çıkardın! Cevabın kesinlikle doğru!
07:30:15
AI Öğretmen
Alanı 72 cm² olan bir dikdörtgenin kenar uzunluklarını bulmak için 72'nin çarpanlarını doğru bir şekilde belirledin.
07:30:16
AI Öğretmen
Bu çarpan çiftlerini kullanarak her bir durum için çevre uzunluğunu hesaplaman ve bunların kaç farklı değer aldığını görmen, problemi çözmedeki anahtar adımlardı.
07:30:17
AI Öğretmen
Bu tür sorularda çarpanları ve çevre formülünü doğru kullanmak çok önemlidir. Tebrikler!
07:30:18
AI Öğretmen
Dolayısıyla doğru cevap 5'tir.
07:30:19
AI Öğretmen
Derse devam edelim mi?
07:30:44
Öğrenci
Olur, devam edelim
07:30:45
💭 AI Öğretmen
Devam edelim o halde
07:30:51
Görsel
Görsel
07:30:54
AI Öğretmen
Bir sayının pozitif tam sayı çarpanlarını bulmak için, 1’den başlayarak o sayıyı kalansız bölen tüm tam sayılar belirlenir.
07:30:56
AI Öğretmen
Şimdi 52 sayısının çarpanlarını adım adım birlikte bulalım.
07:30:58
AI Öğretmen
İlk olarak, 52'yi 1'e böleriz: 52 ÷ 1 = 52, bu yüzden hem 1 hem de 52 çarpandır.
07:31:00
AI Öğretmen
Daha sonra, 52'yi 2'ye böleriz: 52 ÷ 2 = 26, bu durumda da 2 ve 26 çarpandır.
07:31:01
AI Öğretmen
52 sayısı 3’e tam bölünmez, çünkü 52 ÷ 3 işlemi kalansız sonuç vermez.
07:31:02
AI Öğretmen
Sonra, 52'yi 4’e böleriz: 52 ÷ 4 = 13, bu da 4 ve 13’ün çarpan olduğunu gösterir.
07:31:05
AI Öğretmen
52 sayısı 5, 6 ve 7’ye tam bölünmez, yani 52 bu sayılarla bölündüğünde tam sayı bir sonuç elde edemeyiz.
07:31:06
AI Öğretmen
Daha fazla pozitif tam sayı çarpan yoktur, çünkü diğer sayılar 52’yi tam bölemez.
07:31:08
AI Öğretmen
Bu adımlar sonunda, 52 sayısının pozitif tam sayı çarpanları şunlardır: 1, 2, 4, 13, 26 ve 52.
07:31:10
AI Öğretmen
Bir not olarak, pratikte sadece 52’nin karekökü olan yaklaşık 7,2’ye kadar olan sayıları kontrol ederek diğer çarpanları da kolayca bulabiliriz.
07:31:11
AI Öğretmen
Bu çarpanları bulma sürecini anladın mı?
07:32:04
Öğrenci
Anladım
07:32:07
💭 AI Öğretmen
Şimdi bir soruya geçiyoruz
07:32:07
❓ Soru medium
Kenar uzunlukları santimetre cinsinden birer pozitif tam sayı olan bir dikdörtgenin alanı $144 \text{ cm}^2$'dir. Bu bilgilere göre, bu dikdörtgenin çevre uzunluğunun alabileceği en büyük değer ile en küçük değerin farkı kaç santimetredir?
07:35:29
Öğrenci
Cevabım: 228
07:35:30
💭 AI Öğretmen
Hemen Bakıyorum
07:35:36
AI Öğretmen
Cevabınız doğru değil, size nedenini açıklayayım.
07:35:39
AI Öğretmen
Alanı 144 cm² olan bir dikdörtgenin kenar uzunlukları, 144 sayısının pozitif tam sayı çarpanlarıdır. Bu çarpan çiftlerini bulup çevrelerini hesaplamamız gerekiyor.
07:35:41
AI Öğretmen
144 sayısının çarpan çiftleri şunlardır: (1,144), (2,72), (3,48), (4,36), (6,24), (8,18), (9,16), (12,12).
07:35:43
AI Öğretmen
Çevre formülü 2×(a+b) olduğundan, çevreyi en büyük yapmak için kenarların toplamını en büyük, en küçük yapmak için ise toplamı en küçük seçmeliyiz.
07:35:45
AI Öğretmen
En büyük çevre 2×(1+144) = 290 cm, en küçük çevre ise 2×(12+12) = 48 cm olur.
07:35:47
AI Öğretmen
Bu yüzden çevrelerin farkı 290 - 48 = 242 cm olmalıdır. 228 sayısını bulmanız, muhtemelen bazı çarpan çiftlerini atlamanızdan veya çevre hesaplamasında hata yapmanızdan kaynaklanmış olabilir.
07:35:49
AI Öğretmen
Unutmayın, tüm çarpan çiftlerini kontrol etmek ve formülü doğru uygulamak önemli. Böylece doğru sonuca ulaşabilirsiniz.
07:35:49
AI Öğretmen
Başarılarınızın devamını dilerim, matematikte pratik yapmaya devam edin!
07:35:50
AI Öğretmen
Derse devam edelim mi?
07:37:01
Öğrenci
etüt bitti mi
07:37:01
💭 AI Öğretmen
Birazdan kontrol ediyorum
07:37:09
AI Öğretmen
Cevabınız doğru değil, size nedenini açıklayayım.
07:37:11
AI Öğretmen
Soruda, alanı 144 cm² olan ve kenar uzunlukları pozitif tam sayı olan dikdörtgenlerin çevre uzunlukları inceleniyor. Alan, kenarların çarpımıdır, yani \( a \times b = 144 \) olmalıdır.
07:37:15
AI Öğretmen
Burada \(a\) ve \(b\) 144'ün pozitif tam sayı çarpanlarıdır. Bu çarpan çiftlerini bulmamız gerekiyor: (1,144), (2,72), (3,48), (4,36), (6,24), (8,18), (9,16), (12,12).
07:37:24
Öğrenci
Olur, devam edelim
07:37:25
💭 AI Öğretmen
Elbette, devam ediyoruz
07:37:27
AI Öğretmen
Dikdörtgenin çevresi ise \( 2 \times (a + b) \) formülüyle bulunur. En büyük çevre, kenarların toplamının en büyük olduğu durumda, yani (1,144) çiftiyle olur: \( 2 \times (1 + 144) = 290 \).
07:37:30
Görsel
Görsel
07:37:31
AI Öğretmen
En küçük çevre ise kenarların birbirine en yakın olduğu durumda, yani (12,12) çiftiyle olur: \( 2 \times (12 + 12) = 48 \).
07:37:32
AI Öğretmen
Bu iki çevre uzunluğu arasındaki fark \( 290 - 48 = 242 \) cm'dir. Bu yüzden doğru cevap 242'dir.
07:37:32
AI Öğretmen
Bir sayının pozitif tam sayı çarpanları arasında, yalnızca kendisi ve 1 dışında böleni olmayan sayılara asal sayı denir.
07:37:33
AI Öğretmen
Bir sayının asal çarpanları ise, o sayıyı tam bölen asal sayılardır.
07:37:34
AI Öğretmen
Devam edin, böyle sorularla pratik yaptıkça daha iyi anlayacaksınız.
07:37:34
AI Öğretmen
Şimdi daha iyi anladın mı?
07:37:35
AI Öğretmen
Bir sayının asal çarpanlarını bulmak için genellikle bölen listesi yöntemi kullanılır.
07:37:36
AI Öğretmen
Bölen listesi yöntemini kullanarak bir sayının asal çarpanlarını bulmak için önce asal çarpanlarına ayırmak istediğimiz sayıyı yazarız ve yanına dik bir çizgi çekeriz.
07:37:37
AI Öğretmen
Daha sonra bu sayıyı kalansız bölen en küçük asal sayıyı çizginin sağına yazarız ve bölme işlemini başlatırız.
07:37:38
AI Öğretmen
Bölme sonucunu, yani bölünenin bölen asal sayıya böldükten sonra elde edilen sayıyı, çizginin hemen altına, sol tarafa yazarız.
07:37:39
AI Öğretmen
Her seferinde aynı işlemi, sonuç 1 olana kadar, en küçük asal sayılarla bölerek tekrarlamamız gerekir.
07:37:41
AI Öğretmen
Her bölümde, çizginin sağına yazdığımız asal sayılar, o sayının asal çarpanlarını verir.
07:37:42
AI Öğretmen
Örnek olarak 12 sayısının bölen listesiyle asal çarpanlara ayrılması şöyle olur:
07:37:47
AI Öğretmen
Önce 12’yi ikiye böleriz, kalan 6 olur ve çizginin sağına 2 yazarız.
07:37:48
AI Öğretmen
6’yı tekrar ikiye böleriz, kalan 3 olur ve yine iki yazarız.
07:37:50
AI Öğretmen
En son, 3’ü üçe böleriz ve sonuç 1 çıkar, çizginin sağına ise bu kez 3 yazarız.
07:37:53
AI Öğretmen
Sonuçta, 12’nin asal çarpanları 2, 2 ve 3’tür ve bu, 12 = 2 · 2 · 3 şeklinde de gösterilebilir.
07:37:54
AI Öğretmen
Asal çarpanları bulmak için bölen listesi yöntemini anladın mı?
07:38:55
Öğrenci
Anladım
07:38:58
💭 AI Öğretmen
Şimdi bir soruya geçelim
07:38:58
❓ Soru medium
$A$ ve $B$ pozitif tam sayılarının asal çarpanlarına ayrılmış biçimleri aşağıda verilmiştir: $$ A = 2^x \cdot 3^4 \cdot 5^2 $$ $$ B = 2^3 \cdot 3^y \cdot 7^z $$ Bu sayıların en büyük ortak böleni $\text{EBOB}(A, B) = 2^2 \cdot 3^3$ ve en küçük ortak katı $\text{EKOK}(A, B) = 2^3 \cdot 3^4 \cdot 5^2 \cdot 7^5$ olduğuna göre, $x + y + z$ ifadesinin değeri kaçtır?
07:39:54
Öğrenci
Cevabım: 10
07:39:54
💭 AI Öğretmen
Hemen Bakıyorum
07:39:59
AI Öğretmen
Harika bir iş çıkardın! Cevabın kesinlikle doğru!
07:40:01
AI Öğretmen
EBOB ve EKOK'un asal çarpanlara ayrılmış hallerini kullanarak bilinmeyen üsleri bulma konusunda çok başarılısın.
07:40:03
AI Öğretmen
EBOB için ortak asal çarpanların en küçük üssünü, EKOK içinse tüm asal çarpanların en büyük üssünü aldığımızı hatırlamak bu tür soruların anahtarıdır.
07:40:04
AI Öğretmen
Bu bilgileri doğru bir şekilde uygulayarak $x=2$, $y=3$ ve $z=5$ değerlerini buldun.
07:40:06
AI Öğretmen
Dolayısıyla $x+y+z = 2+3+5 = 10$ olur.
07:40:06
AI Öğretmen
Derse devam edelim mi?
07:40:33
Öğrenci
Olur, devam edelim
07:40:34
💭 AI Öğretmen
Hemen devam ediyoruz
07:40:47
AI Öğretmen
Bu derste doğal sayıların pozitif tam sayı çarpanlarını, örneklerle birlikte nasıl bulacağımızı ve asal çarpanlara ayırma yöntemini öğrendik. Ayrıca, çarpanların sayısını ve asal çarpanların nasıl bulunacağını bölen listesi yöntemiyle anlattık. Anladığınız konularla ilgili herhangi bir sorunuz var mı?
07:40:50
AI Öğretmen
Pozitif tam sayı çarpanlarının ne olduğunu, 24 ve 52 gibi sayıların çarpanlarını nasıl bulacağımızı ve asal çarpanlara ayırma yöntemini detaylıca inceledik. Bu bilgiler, matematikte temel kavramlardır ve ilerideki konular için önemlidir. Size açıklamamı istediğiniz bir nokta var mı?
07:40:51
AI Öğretmen
Çarpanlar ve asal çarpanlar konusunu öğrendik, ayrıca asal çarpanlara ayırma işlemini bölen listesi yöntemiyle nasıl yapacağımızı gördük. Bu konularla ilgili kafanıza takılan bir şey var mı? Yoksa dersi burada sonlandırabiliriz.
07:41:49
Öğrenci
sonlandır hocam
07:41:55
AI Öğretmen
Bir sonraki derste görüşmek üzere!

Voltran Okul Analiz Sistemi