← Ana Rapor / TOPRAK ŞEN / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
22 October 2025, 18:09
Bitiş
22 October 2025, 18:27
Süre
18 dakika
Durum
Tamamlandı

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Çarpanlar Ve Katlar
Alt Konular:
  • Pozitif Tam Sayıların Pozitif Tam Sayı Çarpanları
Kazanımlar:
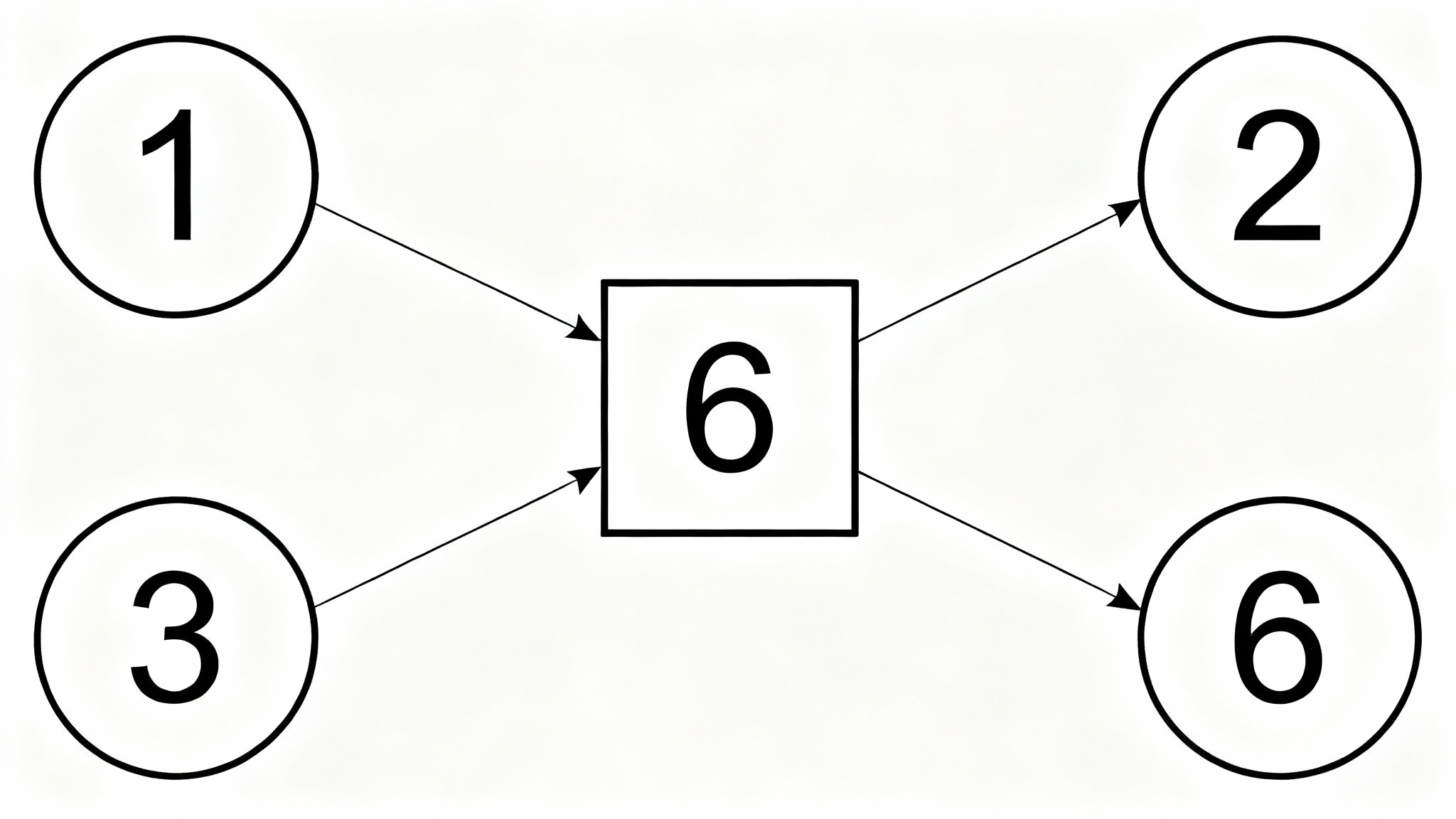
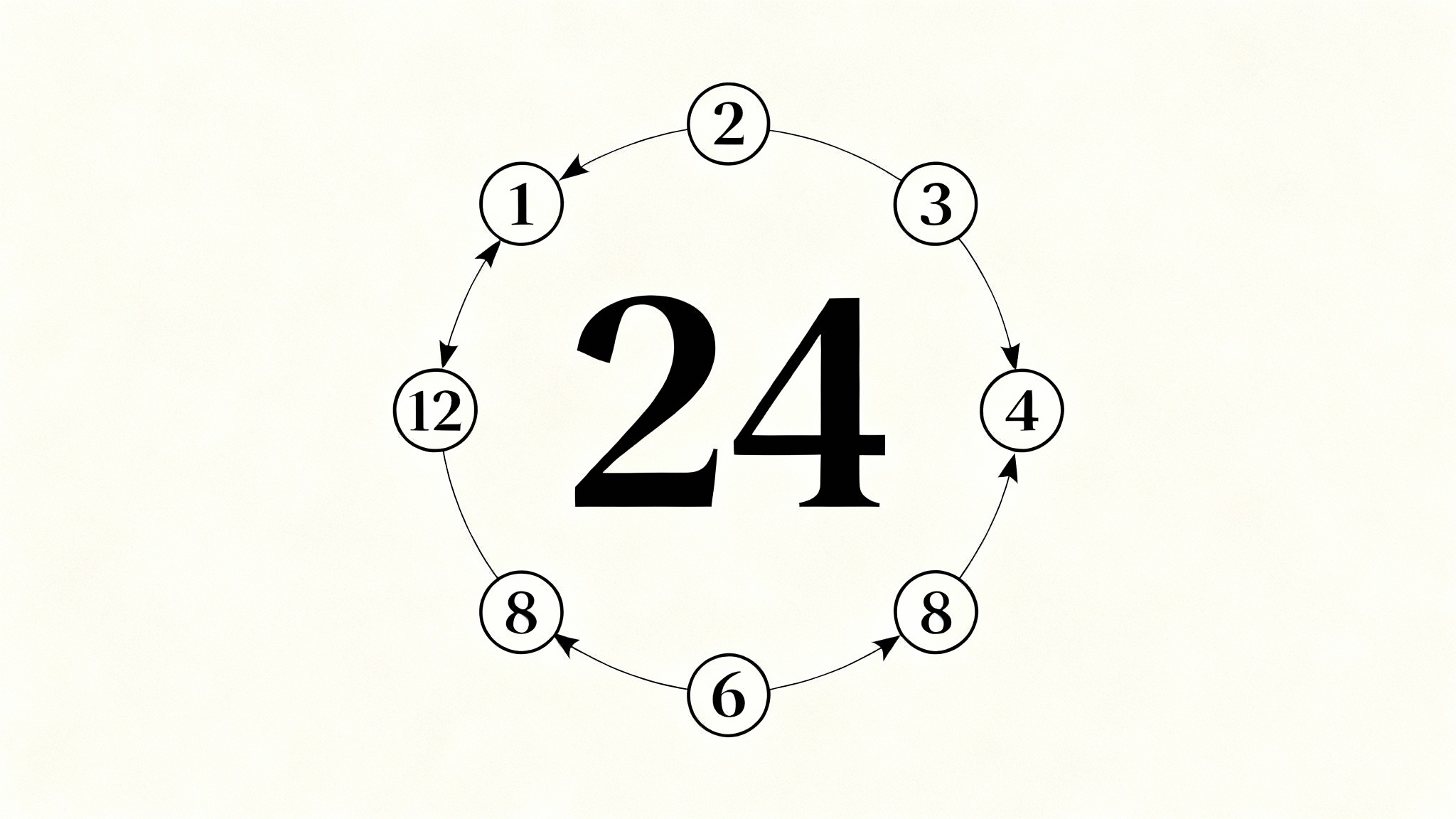
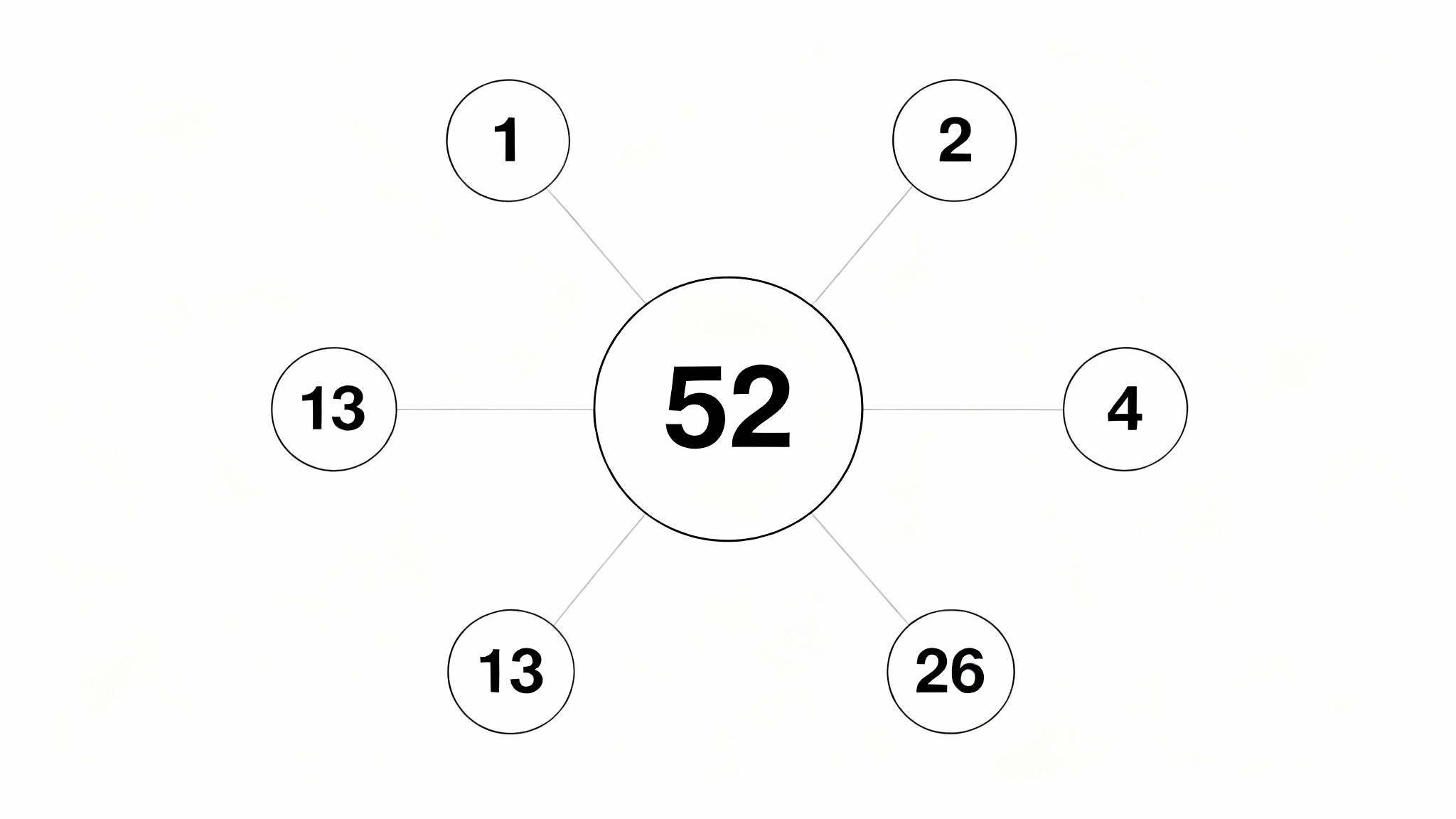
  • Verilen pozitif tam sayıların pozitif tam sayı çarpanlarını bulur, pozitif tam sayıların pozitif tam sayı çarpanlarını üslü ifadelerin çarpımı şeklinde yazar.

Detaylı Değerlendirme

Genel Değerlendirme

Öğrenci ders boyunca ilgili ve katılımcı bir tutum sergiledi. Konunun temel mantığını anladığını belirtse de, bu bilgiyi problem çözümüne aktarmakta zorlandığı gözlemlendi. Özellikle çok adımlı veya dolaylı akıl yürütme gerektiren sorularda hatalar yaptı. Konu anlatımlarından sonra "Anladım" demesine rağmen, takip eden sorularda ipucu istemesi veya yanlış cevaplar vermesi, konunun tam olarak pekişmediğini göstermektedir. Ancak, dersin sonlarına doğru EBOB-EKOK ile ilgili soruyu doğru çözmesi, asal çarpanlar ve üsler arasındaki ilişkiyi anladığını göstermektedir.

Detaylı Analiz

* Başlangıç ve Temel Kavramlar: Öğrenci, dersin başında pozitif tam sayı çarpanları konusunun temel tanımını anladığını belirtmiş ancak ilk soruda hemen ipucu istemiş ve ardından yanlış cevap vermiştir. Bu durum, "çarpan sayısı formülü" gibi teorik bilgileri pratiğe dökmekte zorlandığını göstermektedir.
* Problem Çözme Becerisi: Alanı verilen bir dikdörtgenin çevre uzunluğu ile ilgili sorularda performansı değişkendir. İlk soruda (alanı 72 cm²), sorunun ne istediğini yanlış anlamış ve çevre değerlerini saymak yerine toplamıştır. Ancak, öğretmenin açıklamasından sonra sorulan benzer bir soruyu (alanı 70 cm²) doğru bir şekilde çözmüştür. Bu, öğrencinin açıklamaları dikkatle dinlediğinde ve öğrendiklerini uygulayabildiğini, ancak ilk karşılaşmada problem yorumlama eksiği olduğunu göstermektedir.
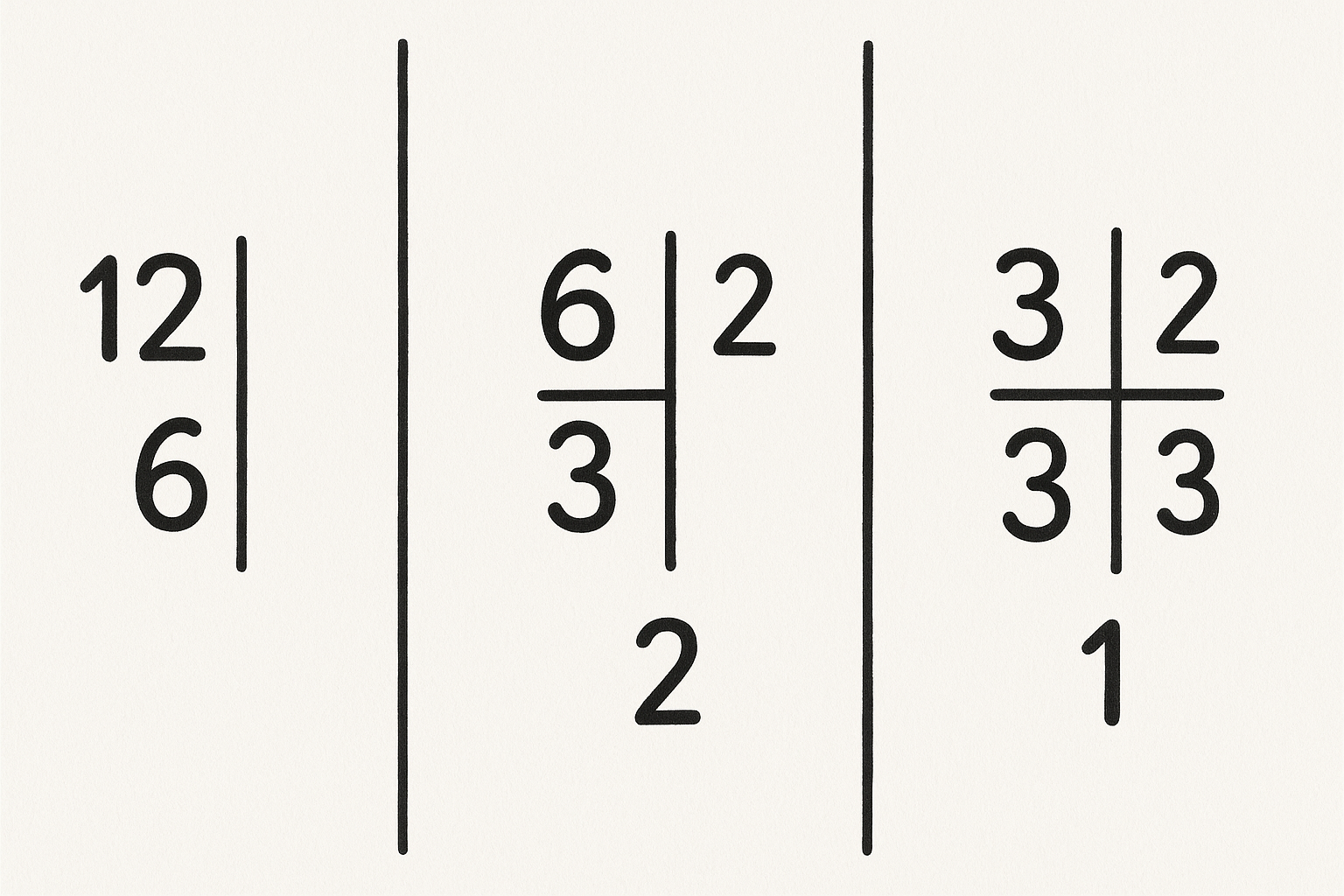
* Asal Çarpanlara Ayırma: Öğrenci, "bölen listesi" yöntemini kullanarak bir sayıyı asal çarpanlarına ayırma konusunda "bu yöntemi tam olarak anlamadım" diyerek açıkça zorlandığını belirtmiştir. Video anlatımı sonrası konuyu anladığını belirtse de bu konudaki becerisi yeni bir soruyla test edilmemiştir.
* EBOB ve EKOK Uygulaması: Dersin en olumlu kısmı, öğrencinin üslü ifadeler şeklinde verilmiş sayıların EBOB ve EKOK'unu kullanarak bilinmeyen üsleri bulduğu soruyu doğru cevaplamasıdır. Bu, öğrencinin EBOB ve EKOK'un temel mantığını ve asal çarpanların üsleriyle olan ilişkisini kavradığını göstermektedir.

Sonuç

Öğrencinin Çarpanlar ve Katlar konusunda temel bir bilgisi olmakla birlikte, özellikle Pozitif Tam Sayıların Pozitif Tam Sayı Çarpanları alt konusunda pratik eksiği bulunmaktadır. Problem çözme ve konuyu farklı soru tiplerine uygulama becerisini geliştirmesi gerekmektedir. EBOB ve EKOK ile ilgili problemleri çözme konusunda ise daha başarılıdır.

📜 Oturum Detayları

18:09:33
Öğrenci
Evet, hazırım Hocam! Bu konuyu detaylıca anlatır mısın?
18:09:34
💭 AI Öğretmen
Hemen başlıyorum
18:09:34
Görsel
Görsel
18:09:37
AI Öğretmen
Her doğal sayı, iki doğal sayının çarpımı şeklinde yazılabilir.
18:09:38
AI Öğretmen
Bu iki sayı, çarpılan sayının çarpanları olarak adlandırılır.
18:09:38
AI Öğretmen
Bir doğal sayının pozitif tam sayı çarpanları, o sayıyı kalansız bölebilen pozitif tam sayılardır.
18:09:40
AI Öğretmen
Yani, pozitif tam sayı çarpanları aslında o sayının bölenleridir.
18:09:41
AI Öğretmen
Çarpanlar konusu, bir sayının hangi sayılara tam olarak bölünebileceğini anlamamıza yardımcı olur.
18:09:42
AI Öğretmen
Örneğin, 6 sayısının çarpanları 1, 2, 3 ve 6'dır.
18:09:43
AI Öğretmen
Bu sayılar, 6'yı kalansız bölebilen pozitif tam sayılardır.
18:09:44
AI Öğretmen
Bir sayının pozitif tam sayı çarpanlarını bulmak, çarpanlar ve katlar konusunun temelini oluşturur.
18:09:45
AI Öğretmen
Çarpanlar konusu hakkında anlattıklarımı anladın mı?
18:10:37
Öğrenci
görseldeki okları anlatır mısın
18:10:41
💭 AI Öğretmen
Biraz düşünelim
18:10:43
AI Öğretmen
Görseldeki oklar, 6 sayısının pozitif tam sayı çarpanlarını gösteriyor.
18:10:44
AI Öğretmen
Oklar, 1, 2, 3 ve 6'nın 6 sayısını böldüğünü ve dolayısıyla 6'nın çarpanları olduğunu anlatıyor.
18:10:45
AI Öğretmen
Yani, oklar sayıları 6'ya bağlayarak bu sayıların 6'nın bölenleri olduğunu simgeliyor.
18:10:46
AI Öğretmen
Bu açıklama senin için anlaşılır oldu mu? Başka bir şey sormak ister misin?
18:11:03
Öğrenci
Anladım
18:11:05
💭 AI Öğretmen
Şimdi biraz pekiştirelim
18:11:06
❓ Soru medium
$A$ pozitif tam sayısının pozitif tam sayı çarpanlarının sayısı $15$'tir. $A \lt 500$ olduğuna göre, $A$'nın alabileceği tüm değerlerin toplamı kaçtır?
18:11:48
Öğrenci
Bir ipucu verir misiniz hocam?
18:11:50
💭 AI Öğretmen
Bir bakalım
18:11:54
AI Öğretmen
Çarpan sayısı 15 olan bir sayının asal çarpanlarının üsleri toplamını nasıl ifade edebiliriz?
18:11:55
AI Öğretmen
15 sayısını çarpan sayısı formülüne göre hangi biçimlerde yazabiliriz?
18:11:56
AI Öğretmen
Bu biçimlerden hangileri 500’den küçük sayılar oluşturabilir?
18:12:40
Öğrenci
Cevabım: 500
18:12:41
💭 AI Öğretmen
Hemen Bakıyorum
18:12:45
AI Öğretmen
Cevabınız doğru değil, size nedenini açıklayayım.
18:12:48
AI Öğretmen
Bir sayının pozitif tam sayı çarpanlarının sayısını bulmak için, sayıyı asal çarpanlarına ayırırız ve üslerine 1 ekleyip çarparız. Örneğin, $A = x^a \cdot y^b$ ise, çarpan sayısı $(a+1)(b+1)$ olur.
18:12:50
AI Öğretmen
Soruda çarpan sayısının 15 olduğu verilmiş. 15 sayısını asal çarpanlara ayırırsak ya $15$ (tek asal kuvvet) ya da $3 \times 5$ (iki asal kuvvet) olarak yazabiliriz.
18:12:52
AI Öğretmen
İlk durumda $A = x^{14}$ olur. En küçük asal sayı 2 için $2^{14} = 16384$ olur ki bu 500'den büyüktür, bu yüzden geçerli değildir.
18:12:53
AI Öğretmen
İkinci durumda ise $A = x^4 \cdot y^2$ veya $A = x^2 \cdot y^4$ şeklindedir. Burada üslerin birisi 4, diğeri 2 olmalıdır.
18:12:57
AI Öğretmen
Şimdi küçük asal sayıları deneyelim: - $2^4 \cdot 3^2 = 16 \cdot 9 = 144$ - $3^4 \cdot 2^2 = 81 \cdot 4 = 324$ - $2^4 \cdot 5^2 = 16 \cdot 25 = 400$ Bunların hepsi 500'den küçüktür ve geçerli çözümlerdir.
18:12:58
AI Öğretmen
Diğer kombinasyonlar 500'den büyük olduğu için kabul edilmez. Böylece $A$'nın alabileceği değerler 144, 324 ve 400'dür.
18:13:00
AI Öğretmen
Bu sayıların toplamı ise $144 + 324 + 400 = 868$ olur.
18:13:02
AI Öğretmen
Sonuç olarak, $A$'nın alabileceği tüm değerlerin toplamı 868'dir. Bu yüzden doğru cevap 868 olmalıdır.
18:13:03
AI Öğretmen
Bu tür sorularda asal çarpanlara ayırma ve çarpan sayısı formülünü dikkatli kullanmak çok önemlidir, böylece doğru sonuçlara ulaşabilirsiniz.
18:13:03
AI Öğretmen
Derse devam edelim mi?
18:14:24
Öğrenci
Olur, devam edelim
18:14:25
💭 AI Öğretmen
Devam etmeye hazırız
18:14:29
Görsel
Görsel
18:14:31
AI Öğretmen
Bir sayının çarpanları, o sayıyı kalansız bölen pozitif tam sayılardır.
18:14:33
AI Öğretmen
Yani, bir sayı başka bir sayıya bölündüğünde sonuç tam çıkıyorsa ve kalan sıfır oluyorsa, bu bölen o sayının çarpanı olur.
18:14:34
AI Öğretmen
24 sayısının çarpanlarını bulmak için çarpan çiftlerini inceleyebiliriz.
18:14:35
AI Öğretmen
Örneğin: 1 ile 24’ü çarptığımızda 1 × 24 = 24.
18:14:36
AI Öğretmen
Aynı şekilde 2 × 12 = 24, 3 × 8 = 24 ve 4 × 6 = 24’tür.
18:14:38
AI Öğretmen
Buradan hareketle, 24'ü kalansız bölen pozitif tam sayılar şunlardır: 1, 2, 3, 4, 6, 8, 12 ve 24.
18:14:39
AI Öğretmen
Bu sayıların her biri, 24'ü başka bir pozitif tam sayı ile çarptığımızda sonucu tam olarak 24 yapan sayılardır.
18:14:40
AI Öğretmen
Örneğin 2 × 12 = 24 olduğu için hem 2 hem de 12, 24'ün çarpanlarıdır.
18:14:43
AI Öğretmen
Aynı şekilde 3 × 8 = 24 ve 4 × 6 = 24 işlemlerini de kontrol ederek diğer çarpanları bulabiliriz.
18:14:44
AI Öğretmen
Sonuç olarak, 24'ü kalansız bölen pozitif tam sayılar 1, 2, 3, 4, 6, 8, 12 ve 24’tür.
18:14:44
AI Öğretmen
Anlattığım çarpanlar konusunu anladın mı?
18:15:31
Öğrenci
Anladım
18:15:35
💭 AI Öğretmen
Şimdi bir soru soracağım
18:15:35
❓ Soru medium
Alanı $72$ cm$^2$ olan bir dikdörtgenin kenar uzunlukları, santimetre cinsinden $1$'den büyük birer tam sayıdır. Bu dikdörtgenin çevre uzunluğunun alabileceği kaç farklı tam sayı değeri vardır?
18:16:49
Öğrenci
Cevabım: 54+76+44+36+146=356
18:16:50
💭 AI Öğretmen
Hemen Bakıyorum
18:16:57
AI Öğretmen
Cevabınız doğru değil, çünkü soruda çevre uzunluklarının toplamı değil, çevrenin alabileceği farklı tam sayı değerlerinin sayısı isteniyor.
18:16:59
AI Öğretmen
Alanı 72 cm² olan dikdörtgenin kenar uzunlukları 1’den büyük tam sayılar olduğuna göre, bu kenarların 72’nin çarpanları olması gerekir. Çarpan çiftlerini bulup, 1’den büyük olanları seçmeliyiz.
18:17:01
AI Öğretmen
Bunlar: (2,36), (3,24), (4,18), (6,12), (8,9) çiftleridir. Her çift için çevre uzunluğu 2 × (a + b) formülüyle hesaplanır.
18:17:03
AI Öğretmen
Çevreler sırasıyla 76, 54, 44, 36 ve 34 cm olur ve bunlar birbirinden farklı 5 tam sayı değeridir.
18:17:04
AI Öğretmen
Öğrenci olarak çevrelerin toplamını almak yerine, bu farklı çevre değerlerinin kaç tane olduğunu saymak gerekiyor. Ayrıca 146 sayısı soruda yok ve yanlış hesaplama sonucu ortaya çıkmış.
18:17:05
AI Öğretmen
Bu yüzden doğru cevap, dikdörtgenin çevre uzunluğunun alabileceği farklı tam sayı değeri sayısı olan 5’tir. Öğrenmeye devam et, böylece benzer sorularda daha dikkatli olabilirsin!
18:17:06
AI Öğretmen
Derse devam edelim mi?
18:17:52
Öğrenci
Olur, devam edelim
18:17:53
💭 AI Öğretmen
Harika, devam ediyoruz
18:18:00
Görsel
Görsel
18:18:02
AI Öğretmen
Bir sayının pozitif tam sayı çarpanlarını bulmak için, 1’den başlayıp o sayıyı tam bölen tüm tam sayıları bulmamız gerekir.
18:18:03
AI Öğretmen
Şimdi 52 sayısının çarpanlarını adım adım bulalım.
18:18:05
AI Öğretmen
Önce 52’yi 1’e bölelim. 52 bölü 1 eşittir 52, bu durumda 1 ve 52 çarpandır.
18:18:06
AI Öğretmen
Şimdi 52’yi 2’ye bölelim. 52 bölü 2 eşittir 26, yani 2 ve 26 da çarpandır.
18:18:07
AI Öğretmen
52’yi 3’e böldüğümüzde kalanlı sonuç çıkar, yani tam bölünmez ve 3 çarpan değildir.
18:18:08
AI Öğretmen
52’yi 4’e bölelim. 52 bölü 4 eşittir 13, o zaman 4 ve 13 de çarpandır.
18:18:09
AI Öğretmen
Şimdi 5, 6 ve 7’yi denersek, 52 bu sayılara tam bölünmez yani onlar çarpan değildir.
18:18:10
AI Öğretmen
Başka çarpan bulamıyoruz. Sonuç olarak, 52’nin pozitif tam sayı çarpanları 1, 2, 4, 13, 26 ve 52’dir.
18:18:12
AI Öğretmen
Not olarak, pratikte sadece $\sqrt{52}$ yani yaklaşık 7,2’ye kadar olan sayıları kontrol ederek diğer çarpanlar da bulunabilir.
18:18:13
AI Öğretmen
Çarpanları bulma yöntemini anladın mı?
18:19:24
Öğrenci
üstte bir soru vardı 72 santimetre kare olan?
18:19:26
💭 AI Öğretmen
Bir bakalım
18:19:30
AI Öğretmen
Alanı 72 cm² olan dikdörtgenin kenar uzunlukları 1’den büyük tam sayılar olduğunda, bu kenarlar 72’nin 1’den büyük çarpanlarıdır.
18:19:31
AI Öğretmen
Bu çarpan çiftleri: (2,36), (3,24), (4,18), (6,12) ve (8,9) şeklindedir.
18:19:33
AI Öğretmen
Her çift için çevre uzunluğu $2 \times (a + b)$ formülüyle hesaplanır ve farklı çevre uzunlukları bulunur.
18:19:34
AI Öğretmen
Bu çevre uzunlukları sırasıyla 76, 54, 44, 36 ve 34’tür.
18:19:36
AI Öğretmen
Yani, dikdörtgenin çevre uzunluğunun alabileceği 5 farklı tam sayı değeri vardır.
18:19:37
AI Öğretmen
Anladın mı? Başka sorun var mı?
18:20:31
Öğrenci
34 nereden geldidiye soracaktım fakat anladım teşekkürler
18:20:33
💭 AI Öğretmen
Güzel, şimdi devam edelim
18:20:33
❓ Soru medium
Kenar uzunlukları santimetre cinsinden birer pozitif tam sayı olan bir dikdörtgenin alanı $144 \text{ cm}^2$'dir. Bu bilgilere göre, bu dikdörtgenin çevre uzunluğunun alabileceği en büyük değer ile en küçük değerin farkı kaç santimetredir?
18:21:28
Öğrenci
Cevabım: 290-48=242
18:21:29
💭 AI Öğretmen
Hemen Bakıyorum
18:21:34
AI Öğretmen
Harika bir iş çıkardın! Cevabın tamamen doğru.
18:21:35
AI Öğretmen
Dikdörtgenin alanını oluşturan çarpan çiftlerini bularak, kenar uzunlukları arasındaki farkın çevreyi nasıl etkilediğini çok iyi anlamışsın.
18:21:36
AI Öğretmen
Kenarlar ne kadar farklı olursa çevre o kadar büyük, ne kadar birbirine yakın olursa çevre o kadar küçük olur.
18:21:37
AI Öğretmen
Bu problemde en büyük çevre 290 cm ve en küçük çevre 48 cm'dir. Farkları ise 242 cm'dir.
18:21:38
AI Öğretmen
Doğru cevap 242'dir.
18:21:38
AI Öğretmen
Derse devam edelim mi?
18:22:04
Öğrenci
Olur, devam edelim
18:22:05
💭 AI Öğretmen
Tamam, devam ediyorum
18:22:11
Görsel
Görsel
18:22:13
AI Öğretmen
Bir sayının asal çarpanları, o sayının pozitif tam sayı çarpanları arasında, kendisi dışında başka pozitif böleni olmayan asal sayılardır.
18:22:14
AI Öğretmen
Asal çarpanlar, verilen sayıyı tam olarak bölen asal sayılardır.
18:22:15
AI Öğretmen
Bir sayının asal çarpanlarını bulmak için en çok kullanılan yöntemlerden biri bölen listesi yöntemidir.
18:22:16
AI Öğretmen
Bölen listesi yönteminde, önce asal çarpanlarına ayırmak istediğimiz sayıyı yazar ve yanına dik bir çizgi çekeriz.
18:22:18
AI Öğretmen
Bu sayıyı kalansız bölen en küçük asal sayıyı, çizginin sağına yazarak bölme işlemini başlatırız.
18:22:19
AI Öğretmen
Bulduğumuz sonucu, çizginin solundaki sayının altına yazarız.
18:22:20
AI Öğretmen
Sonuç 1 olana kadar aynı işlemi tekrarlayarak, her seferinde asal sayılarla bölmeye devam ederiz.
18:22:20
AI Öğretmen
Çizginin sağına yazdığımız asal sayıları listeleriz.
18:22:21
AI Öğretmen
Örneğin, 12 sayısı için bölen listesi yöntemi şöyle uygulanır:
18:22:22
AI Öğretmen
12'nin yanına bir çizgi çekeriz ve 12'yi bölen en küçük asal sayı olan 2'yi sağ tarafa yazarız, 12'yi 2'ye böleriz ve 6 buluruz.
18:22:24
AI Öğretmen
6'nın altına yazarız ve tekrar en küçük asal sayı olan 2'yle böleriz, 6'yı 2'ye böldüğümüzde 3 elde ederiz.
18:22:25
AI Öğretmen
En son 3'ü, asal sayı olan 3'e böleriz ve 1 elde ederiz.
18:22:26
AI Öğretmen
Sonuç olarak, asal çarpanları 2, 2 ve 3 olur ve 12 = 2·2·3 şeklinde ifade edilir.
18:22:27
AI Öğretmen
Bölen listesi yöntemiyle asal çarpanları bulma kısmını anladın mı?
18:23:41
Öğrenci
bu yöntemi tam olarak anlamadım
18:23:44
💭 AI Öğretmen
Konuyu yeniden ele alıyoruz
18:23:44
🎥 Video
18:23:45
AI Öğretmen
Bölen listesi yöntemiyle asal çarpanları bulmayı şimdi daha iyi anladın mı?
18:25:13
Öğrenci
Anladım
18:25:17
💭 AI Öğretmen
Şimdi size bir soru yönelteceğim
18:25:17
❓ Soru medium
$A$ ve $B$ pozitif tam sayılarının asal çarpanlarına ayrılmış biçimleri aşağıda verilmiştir: $$ A = 2^x \cdot 3^4 \cdot 5^2 $$ $$ B = 2^3 \cdot 3^y \cdot 7^z $$ Bu sayıların en büyük ortak böleni $\text{EBOB}(A, B) = 2^2 \cdot 3^3$ ve en küçük ortak katı $\text{EKOK}(A, B) = 2^3 \cdot 3^4 \cdot 5^2 \cdot 7^5$ olduğuna göre, $x + y + z$ ifadesinin değeri kaçtır?
18:25:50
Öğrenci
Cevabım: 10
18:25:50
💭 AI Öğretmen
Hemen Bakıyorum
18:25:55
AI Öğretmen
Harika bir iş çıkardın! Cevabın kesinlikle doğru!
18:25:56
AI Öğretmen
EBOB ve EKOK'un asal çarpanlara ayrılmış hallerini kullanarak üsleri doğru bir şekilde eşleştirdin.
18:25:57
AI Öğretmen
EBOB için en küçük üssü, EKOK için en büyük üssü alarak bilinmeyenleri bulman, bu konuyu ne kadar iyi anladığını gösteriyor.
18:25:58
AI Öğretmen
Bu tür sorular, asal çarpanlara ayırma ve üslü sayılar bilginin ne kadar sağlam olduğunu kanıtlıyor!
18:25:58
AI Öğretmen
Dolayısıyla doğru cevap 10'dur.
18:25:59
AI Öğretmen
Derse devam edelim mi?
18:26:25
Öğrenci
Olur, devam edelim
18:26:25
💭 AI Öğretmen
Tamam, hemen devam ediyoruz
18:26:37
AI Öğretmen
Bu derste doğal sayıların pozitif tam sayı çarpanları ve asal çarpanları konularını ele aldık. Çarpanların nasıl bulunacağını, özellikle 24 ve 52 sayıları üzerinden örneklerle gösterdik. Ayrıca asal çarpanları bulmak için bölen listesi yöntemini anlattık. Anlamadığın veya sormak istediğin bir şey var mı?
18:27:12
Öğrenci
çok güzel anlattınız hocam teşekkür ederim
18:27:16
AI Öğretmen
Bir sonraki derste görüşmek üzere!

Voltran Okul Analiz Sistemi