← Ana Rapor / KAYA ALP YILDIRIM / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
10 December 2025, 19:51
Bitiş
Devam ediyor
Süre
27 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Üçgen

Detaylı Değerlendirme

Öğrenci Performans Analizi

Öğrencinin ders performansında değişken bir başarı gözlemlenmiştir. Üçgenin iç açıları toplamının 180° olduğu temel kuralını anladığı ve uygulayabildiği görülmektedir. Ancak, üçgenleri açılarına göre sınıflandırma konusunda belirgin bir kavram yanılgısı yaşamaktadır.

# Başarılı Olduğu Alanlar
* Üçgenin İç Açıları Toplamı: Öğrenci, bir üçgenin iç açılarının toplamının 180° olduğu kuralını iyi bir şekilde kavramıştır.
* Dersin başında, bir üçgende neden iki dik açı olamayacağını "3. açısı 0 derece olurdu" şeklinde doğru bir mantıkla açıklamıştır.
* Dersin ilerleyen bölümünde, cebirsel ifade içeren bir problemde verilmeyen açıları doğru bir şekilde hesaplayarak (Cevap: 15 derece) bu kuralı karmaşık problemlere de uygulayabildiğini göstermiştir.

# Geliştirilmesi Gereken Alanlar
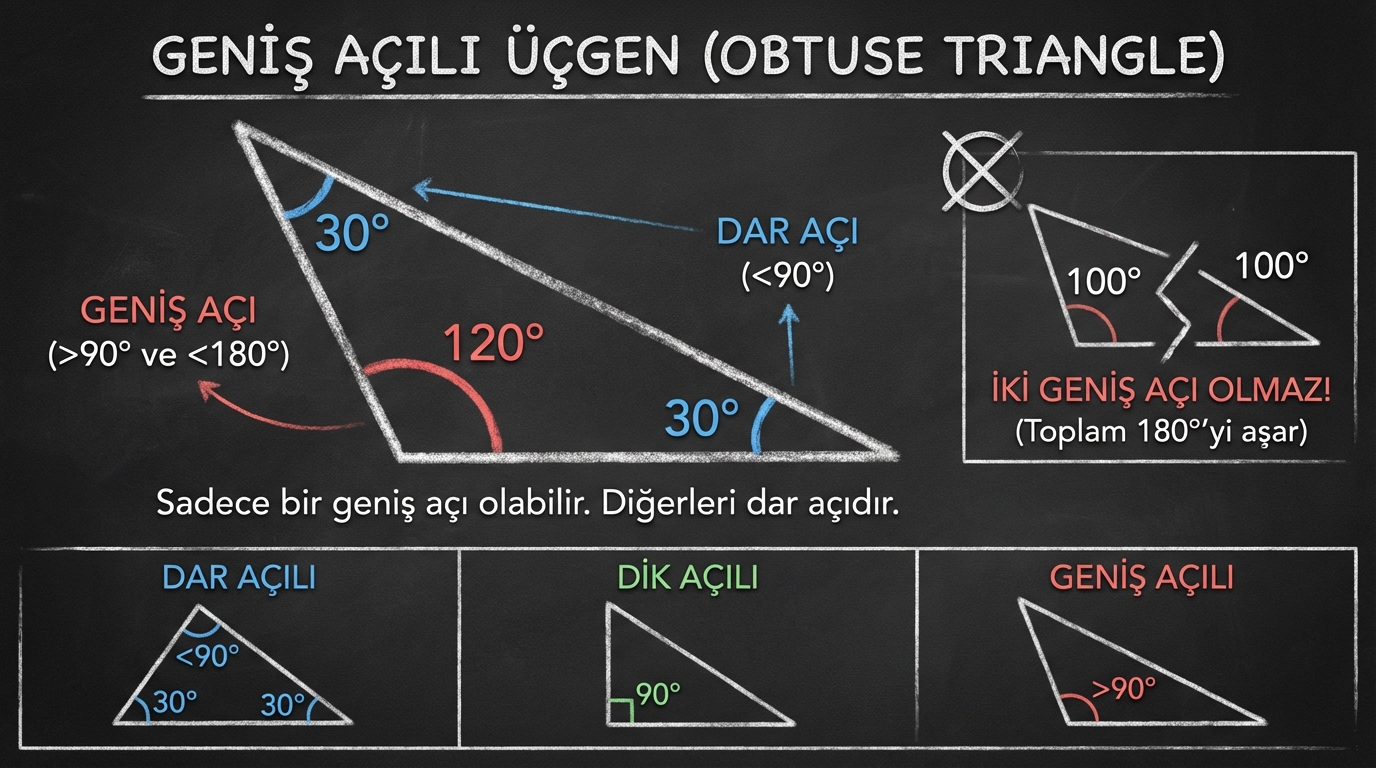
* Üçgenleri Açılarına Göre Sınıflandırma: Öğrencinin en temel eksikliği, dar açılı ve geniş açılı üçgen tanımlarını karıştırmasıdır.
* İki açısı 55° ve 65° olan bir üçgen sorulduğunda, üçüncü açıyı (60°) hesaplamak yerine doğrudan "bu bir geniş açılı üçgendir" şeklinde yanlış bir cevap vermiştir.
* Cevabına gerekçe olarak sunduğu "dar açılı olsaydı bu sayıların toplamı 90 üstü olmazdı" ifadesi, dar açı tanımını (tüm açıların 90°'den küçük olması) anlamadığını ve kavramları birbiriyle karıştırdığını göstermektedir. Bu konu üzerinde tekrar durulması ve bol örnek çözülmesi faydalı olacaktır.

# Genel Değerlendirme
Öğrenci, temel hesaplama becerilerine sahip olmakla birlikte, geometrik kavramların tanımlarını ve özelliklerini ezberlemek yerine mantığını anlama konusunda desteğe ihtiyaç duymaktadır. Özellikle üçgen çeşitleri arasındaki farklar netleştirilmelidir.

📜 Oturum Detayları

19:51:58
Öğrenci
Evet, hazırım Hocam! Bu konuyu detaylıca anlatır mısın?
19:51:58
💭 AI Öğretmen
Harika, başlıyoruz
19:52:00
AI Öğretmen
Üçgen, üç kenarı ve üç köşesi olan kapalı bir şekildir.
19:52:01
AI Öğretmen
Üçgenler, köşelerindeki açıların büyüklüklerine bakılarak sınıflandırılır.
19:52:03
AI Öğretmen
Üçgenlerin sınıflandırılmasında, özellikle açılarına göre ayrım yapılır.
19:52:04
AI Öğretmen
Dik açılı üçgen ise, köşelerinden sadece birinin $90°$ olduğu üçgendir.
19:52:05
AI Öğretmen
$90°$ olan bu açıya dik açı denir.
19:52:06
AI Öğretmen
Örneğin, defterin köşesi bir dik açıya örnek olarak düşünülebilir.
19:52:08
AI Öğretmen
Eğer üçgenin bir köşesi de böyleyse, bu üçgen dik açılıdır.
19:52:08
AI Öğretmen
Bir üçgende iki tane dik açı olamaz.
19:52:09
AI Öğretmen
Çünkü üçgenin iç açıları toplamı $180°$’dir.
19:52:12
AI Öğretmen
Eğer iki açı $90°$ olsaydı $90° + 90° = 180°$ olurdu ve üçüncü açıya hiç yer kalmazdı.
19:52:12
AI Öğretmen
Bu kısmı anladın mı?
19:53:51
Öğrenci
Anladım
19:53:53
💭 AI Öğretmen
Şimdi bir soruya geçiyoruz
19:53:54
❓ Soru medium
Aslı, bir üçgenin iç açılarından ikisinin 90° olabileceğini iddia ediyor ve böyle bir üçgen çizmeye çalışıyor. Aslı'nın bu iddiasının geometrik olarak neden yanlış olduğunu üçgenin iç açıları toplamı kuralını kullanarak açıklayınız. Eğer bir üçgenin iki açısı gerçekten 90° olsaydı, üçüncü açının ölçüsü kaç derece olurdu ve bu durum neden bir üçgen oluşturmazdı?
19:54:48
Öğrenci
Cevabım: 3. açısı 0 derece olurdu ayrıca 2 açı 90 olamaz
19:54:49
💭 AI Öğretmen
Hemen Bakıyorum
19:54:53
AI Öğretmen
Harika bir cevap! Tam isabet!
19:54:56
AI Öğretmen
Üçgenlerin iç açılarının toplamının 180° olduğunu çok iyi biliyorsun. Eğer iki açı 90° olsaydı, üçüncü açıya 0° kalırdı ki bu da bir üçgen oluşturmazdı.
19:54:57
AI Öğretmen
Bu temel kuralı anlaman, geometri problemlerini çözmende sana çok yardımcı olacak. Tebrikler!
19:54:58
AI Öğretmen
Derse devam edelim mi?
19:55:19
Öğrenci
Olur, devam edelim
19:55:20
💭 AI Öğretmen
Tamam, devam ediyoruz
19:55:34
AI Öğretmen
Dar açılı üçgen, üçgen çeşitlerinden biridir ve açılarına göre adlandırılır.
19:55:35
AI Öğretmen
Bir üçgenin dar açılı olabilmesi için, üç tane açısının da 90 dereceden küçük olması gerekir.
19:55:36
AI Öğretmen
Dar açılı üçgenlerde, bütün köşeler sivri olur ve hiçbiri dik açı (90°) veya geniş açı (90°'den büyük) olamaz.
19:55:37
AI Öğretmen
Bir üçgenin sadece bir ya da iki açısı dar açıysa, o üçgen dar açılı üçgen sayılmaz, çünkü üç açının da dar açı olması zorunludur.
19:55:39
AI Öğretmen
Eğer üçgenin iki açısı dar, bir açısı dik ise bu üçgen dar açılı üçgen değil, dik açılı üçgendir.
19:55:40
AI Öğretmen
Sonuç olarak, dar açılı üçgenlerde tüm açıların 90 dereceden küçük olması ve köşelerinin oldukça sivri, yani sıkışmış gibi görünmesi gerekir.
19:55:41
AI Öğretmen
Dar açılı üçgenlerle ilgili bu kısmı anladın mı?
19:56:29
Öğrenci
Anladım
19:56:32
💭 AI Öğretmen
Şimdi konuyu pekiştirelim
19:56:32
❓ Soru medium
Bir üçgenin iç açılarından ikisinin ölçüsü 55° ve 65°'dir. Bu üçgenin açılarına göre türünü belirleyiniz ve nedenini açıklayınız.
19:59:18
Öğrenci
Cevabım: bu bir geniş açılı üçgendir çünkü dar açılı olsaydı bu sayıların toplamı 90 üstü olmazdı
19:59:19
💭 AI Öğretmen
Hemen Bakıyorum
19:59:24
AI Öğretmen
Cevabınız doğru değil, çünkü üçgenin geniş açılı olduğunu söylemişsiniz ama verilen açıların toplamını tam olarak hesaplamamışsınız.
19:59:26
AI Öğretmen
Bir üçgenin iç açılarının toplamı her zaman 180°'dir. İlk iki açıyı toplarsak 55° + 65° = 120° olur.
19:59:28
AI Öğretmen
Üçüncü açıyı bulmak için 180°'den 120°'yi çıkarırız, bu da 60° yapar. Böylece açıların hepsi 90°'den küçüktür.
19:59:30
AI Öğretmen
Bir üçgenin dar açılı olması için tüm açıların 90°'den küçük olması gerekir. Bu yüzden bu üçgen dar açılıdır.
19:59:31
AI Öğretmen
Yanlış anlamanız muhtemelen "dar açılı" ve "geniş açılı" terimlerini karıştırmanızdan kaynaklanıyor olabilir.
19:59:34
AI Öğretmen
Örnek olarak, eğer bir açınız 90°'den büyük olsaydı o zaman üçgen geniş açılı olurdu. Ama burada öyle değil.
19:59:35
AI Öğretmen
Bu yüzden doğru cevap, bu üçgenin dar açılı üçgen olduğudur.
19:59:35
AI Öğretmen
Derse devam edelim mi?
20:01:16
Öğrenci
Olur, devam edelim
20:01:17
💭 AI Öğretmen
Devam ediyorum
20:01:25
Görsel
Görsel
20:01:28
AI Öğretmen
Bir üçgenin açılarından birinin 90 dereceden büyük olması durumunda bu üçgene geniş açılı üçgen adı verilir.
20:01:30
AI Öğretmen
Geniş açı, ölçüsü 90 derece ile 180 derece arasında olan açıdır; bu yüzden geniş açılı üçgenin bir köşesi diğerlerine göre daha açık ve yayvan görünür.
20:01:33
AI Öğretmen
Üçgenin iç açılarının toplamı her zaman 180 derece olduğu için, bir üçgende iki tane geniş açı olamaz; çünkü iki geniş açının toplamı zaten 180 dereceyi bulur veya geçer ve üçüncü bir açıya yer kalmaz.
20:01:35
AI Öğretmen
Bu yüzden geniş açılı üçgenlerde yalnızca bir tane geniş açı bulunur, diğer iki iç açı ise mutlaka dar açı olmak zorundadır.
20:01:36
AI Öğretmen
Geniş açılı üçgenler, üçgenlerin iç açılarına göre yapılan sınıflamada dar açılı ve dik üçgenlerle birlikte temel üçgen türlerinden biridir.
20:01:37
AI Öğretmen
Geniş açılı üçgenler hakkında anlattıklarımı anladın mı?
20:04:12
Öğrenci
Anladım
20:04:15
💭 AI Öğretmen
Şimdi biraz düşünelim
20:04:15
❓ Soru medium
Bir KLM üçgeni geniş açılı bir üçgendir. Bu üçgenin en büyük açısının ölçüsü 110°'dir. Diğer iki açıdan birinin ölçüsü diğerinin 3 katından 10° fazla olduğuna göre, bu üçgenin en küçük açısı kaç derecedir?
20:06:01
Öğrenci
Cevabım: 15 derecedir
20:06:02
💭 AI Öğretmen
Hemen Bakıyorum
20:06:06
AI Öğretmen
Harika bir iş çıkardın! Cevabın kesinlikle doğru!
20:06:08
AI Öğretmen
Bir üçgenin iç açılarının toplamının 180° olduğunu ve cebirsel denklemlerle bilinmeyen açıları nasıl bulabileceğini çok iyi göstermişsin.
20:06:09
AI Öğretmen
Bu problemde, geniş açıyı ve diğer iki açının toplamını doğru bir şekilde belirleyip denklemi kurarak en küçük açıyı buldun.
20:06:11
AI Öğretmen
Açıları ve denklemleri birleştirmekte ne kadar başarılı olduğunu görmek harika!
20:06:12
AI Öğretmen
Doğru cevap 15 derecedir.
20:06:12
AI Öğretmen
Derse devam edelim mi?
20:10:46
Öğrenci
Olur, devam edelim
20:10:51
💭 AI Öğretmen
Harika, sıradaki konuya geçiyoruz
20:10:58
AI Öğretmen
Her üçgende geçerli olan en önemli kural, iç açılarının toplamının daima $180^\circ$ olmasıdır.
20:10:59
AI Öğretmen
Üçgenin çeşidi ne olursa olsun, yani dar açılı, dik açılı ya da geniş açılı olsa da, üç iç açısının ölçüleri toplandığında sonuç her zaman $180^\circ$ çıkar.
20:11:01
AI Öğretmen
Bir üçgende iki iç açının ölçüsünü biliyorsak, bunları toplarız, sonra $180^\circ$’den bu toplamı çıkarırız.
20:11:02
AI Öğretmen
Böylece kalan değer bize üçüncü açının ölçüsünü verir.
20:11:04
AI Öğretmen
Eğer iç açılardan biri $90^\circ$ ise o üçgen “dik üçgen” olur.
20:11:05
AI Öğretmen
Üç açının da ölçüsü $90^\circ$’den küçükse “dar açılı üçgen” adını alır.
20:11:06
AI Öğretmen
Bir iç açısı $90^\circ$’den büyükse ise bu üçgene “geniş açılı üçgen” denir.
20:11:07
AI Öğretmen
İster dar, ister dik, ister geniş açılı olsun, hepsinin ortak özelliği; iç açıların toplamı $180^\circ$’dir.
20:11:08
AI Öğretmen
Üçgenlerin iç açılarının toplamının 180 derece olduğunu anladın mı?
20:25:36
Öğrenci
Evet, hazırım Hocam! Bu konuyu detaylıca anlatır mısın?
20:25:37
💭 AI Öğretmen
Hemen başlıyoruz
20:25:41
AI Öğretmen
Üçgenin iç açılarının toplamının her zaman 180 derece olduğunu söyledik, değil mi? Bu kural, üçgenin türü ne olursa olsun geçerlidir.
20:25:44
AI Öğretmen
Örneğin, bir üçgende iki açıyı biliyorsak, bu iki açının toplamını 180’den çıkararak üçüncü açıyı bulabiliriz. Mesela, bir üçgenin iki açısı 50° ve 60° ise, üçüncü açı 180 - (50 + 60) = 70° olur.
20:25:46
AI Öğretmen
Ayrıca, üçgenin türünü belirlemek için iç açılara bakarız: Eğer bir açı 90° ise üçgen dik açılıdır; tüm açılar 90°'den küçükse dar açılıdır; bir açı 90°'den büyükse geniş açılıdır. Anladın mı?
20:32:54
Öğrenci
Anladım
20:32:57
💭 AI Öğretmen
Şimdi bir soru soracağım
20:32:57
❓ Soru medium
Bir ABC üçgeninde A açısının ölçüsü 62° ve B açısının ölçüsü 48°'dir. Ali, C açısının ölçüsünü bulmak için şu işlemi yapmıştır: Önce 62 ile 48'i toplayarak 110 bulmuş, sonra da 180'den 110'u çıkararak sonucu 80° olarak hesaplamıştır. Ancak Ali'nin çıkarma işleminde bir hata vardır. Ali'nin hatasını düzelterek C açısının doğru ölçüsünü bulunuz ve bu üçgenin açılarına göre türünü (dar açılı, dik açılı, geniş açılı) belirtiniz.

Voltran Okul Analiz Sistemi