← Ana Rapor / AZRA ULUBAY / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
15 December 2025, 16:18
Bitiş
Devam ediyor
Süre
50 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Üçgen

Detaylı Değerlendirme

Öğrenci Performans Analizi

Genel Değerlendirme:
Öğrenci, üçgenlerin temel özellikleri ve açılarına göre sınıflandırılması konusunda temel bir anlayışa sahiptir. Üçgenin iç açılarının toplamının 180° olduğu kuralını bilmekte ve basit hesaplamalarda bu kuralı doğru bir şekilde uygulayabilmektedir. Ancak, geometrik bir durumun neden imkansız olduğunu mantıksal olarak açıklama ve bilgiyi cebirsel ifadeler içeren daha karmaşık problem senaryolarına uygulama konusunda zorluklar yaşamaktadır.

Hangi Konularda Eksiklikleri Var?
Öğrencinin "Üçgen" konusunda temel bilgileri olsa da, bu bilgileri problem çözmede kullanırken zorlandığı görülmüştür.
* Problem Çözme ve Mantıksal Akıl Yürütme: Bir üçgende neden iki dik açı olamayacağı sorulduğunda, temel fikri (açıların toplamının 180° olması) anlamış olsa da açıklamasını net bir şekilde ifade edememiştir.
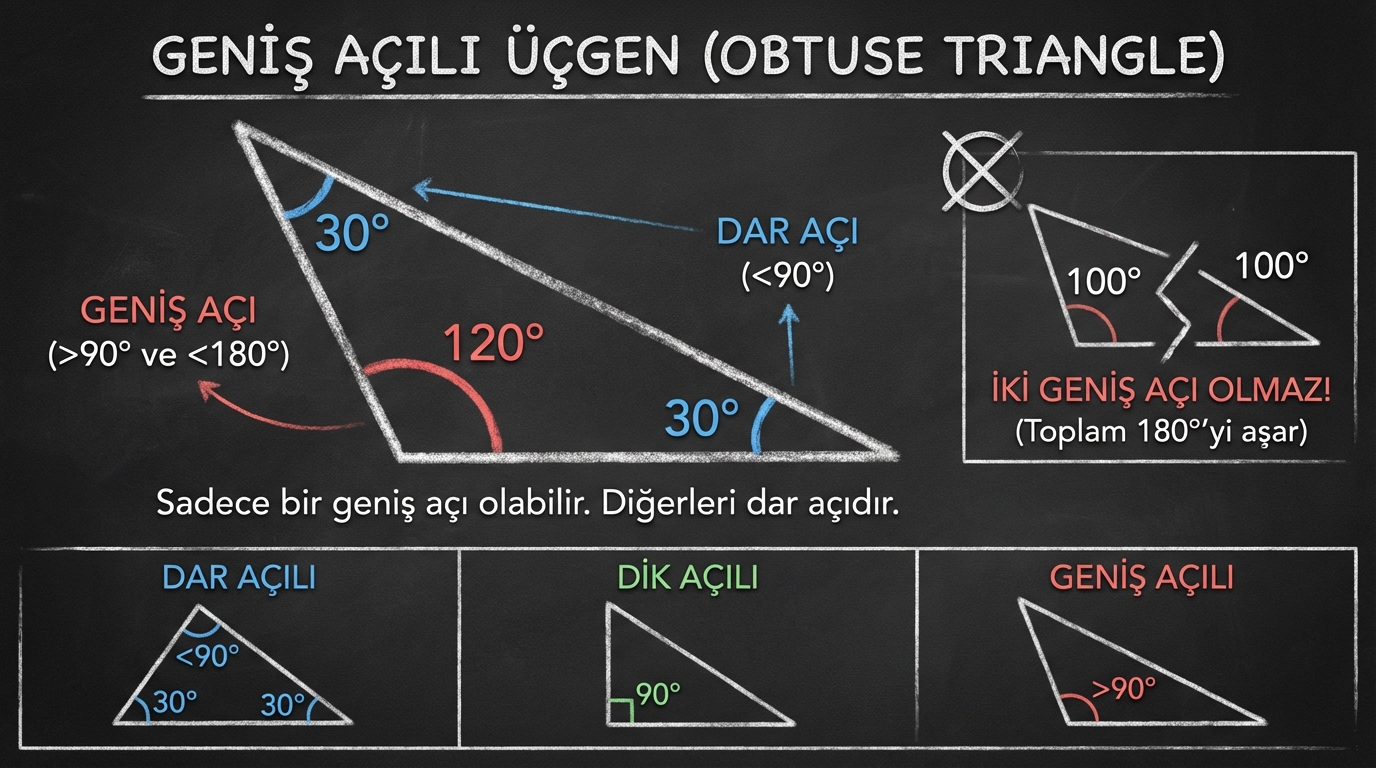
* Cebirsel Uygulama: Geniş açılı üçgenle ilgili soruda, problemi çözmek için ipucu istemiş ve ipucuna rağmen denklemi kurup doğru sonuca ulaşamamıştır. Bu durum, geometrik bilgiyi cebirsel problem çözme adımlarına dönüştürmede eksiklik olduğunu göstermektedir.

Hangi Konularda İyi?
Öğrenci, temel tanımları ve doğrudan hesaplamaları yapabildiği konularda başarılıdır.
* Temel Kavramlar ve Hesaplama: Kendisine iki açısı verilen bir üçgenin üçüncü açısını doğru bir şekilde hesaplamış ve tüm açıların 90 dereceden küçük olduğunu belirterek üçgeni "dar açılı üçgen" olarak doğru bir şekilde sınıflandırmıştır. Bu, temel tanımları ve üçgenin iç açıları toplamı kuralını anladığını göstermektedir.

Tamamen Ders Dışı Sorular/Yorumlar:
Ders sırasında konu dışı herhangi bir yorum veya soru kaydedilmemiştir.

📜 Oturum Detayları

16:18:35
Öğrenci
Evet, hazırım Hocam! Bu konuyu detaylıca anlatır mısın?
16:18:37
💭 AI Öğretmen
Güzel, başlayalım
16:18:39
AI Öğretmen
Üçgen, üç kenarı ve üç köşesi olan kapalı bir şekildir.
16:18:40
AI Öğretmen
Üçgenler, köşelerindeki açı ölçülerine göre sınıflara ayrılır.
16:18:41
AI Öğretmen
Bu sınıflandırmada üçgenlerin açıları önemlidir.
16:18:42
AI Öğretmen
Dik açılı üçgen, köşelerinden sadece bir tanesi $90°$ olan üçgendir.
16:18:43
AI Öğretmen
$90°$ olan açıya dik açı denir.
16:18:44
AI Öğretmen
Bir defterin köşesi bir dik açıya örnektir.
16:18:46
AI Öğretmen
Eğer bir üçgenin bir köşesi defterin köşesi gibi $90°$ ise, o üçgen dik açılıdır.
16:18:46
AI Öğretmen
Bir üçgende iki tane dik açı olamaz.
16:18:47
AI Öğretmen
Bir üçgendeki iç açılar toplandığında $180°$ olur.
16:18:49
AI Öğretmen
Eğer iki açı $90°$ olsaydı, $90° + 90° = 180°$ ederdi ve üçüncü bir açıya yer kalmazdı.
16:18:50
AI Öğretmen
Buraya kadar anlattıklarımı anladın mı?
16:19:21
Öğrenci
Evet, kaldığımız yerden devam edelim hocam!
16:19:21
💭 AI Öğretmen
En son kaldığımız yeri hızlıca bir tekrar edelim
16:19:24
AI Öğretmen
Üçgen, üç tane kenarı ve üç tane köşesi olan kapalı bir şekildir.
16:19:29
AI Öğretmen
Üçgenler, köşelerindeki açıların büyüklüklerine göre farklı gruplara ayrılabilir.
16:19:31
AI Öğretmen
Özellikle açılara göre sınıflandırma yapıldığında, üçgenler içinde özel bir grup olan dik açılı üçgen karşımıza çıkar.
16:19:32
AI Öğretmen
Dik açılı üçgende, köşelerden sadece bir tanesinin ölçüsü $90°$ olur.
16:19:33
AI Öğretmen
$90°$'lik açıya dik açı adı verilir.
16:19:34
AI Öğretmen
Mesela bir defterin köşesini düşün, bu köşe tam $90°$'dir yani dik açıdır ve üçgende de eğer köşe böyleyse o üçgen dik açılı üçgendir.
16:19:35
AI Öğretmen
Bir üçgenin içinde yalnızca bir tane dik açı olabilir.
16:19:36
AI Öğretmen
Çünkü bir üçgendeki bütün iç açıların toplamı $180°$ olmalıdır.
16:19:38
AI Öğretmen
Eğer bu üçgende iki tane dik açı olsaydı, $90° + 90° = 180°$ olurdu ve üçüncü açıya hiç yer kalmazdı.
16:19:39
AI Öğretmen
Şimdi dik açılı üçgenlerle ilgili konuyu daha iyi anladınız mı?
16:20:20
Öğrenci
Anladım
16:20:23
💭 AI Öğretmen
Güzel, devam edelim
16:20:23
❓ Soru medium
Aslı, bir üçgenin iç açılarından ikisinin 90° olabileceğini iddia ediyor ve böyle bir üçgen çizmeye çalışıyor. Aslı'nın bu iddiasının geometrik olarak neden yanlış olduğunu üçgenin iç açıları toplamı kuralını kullanarak açıklayınız. Eğer bir üçgenin iki açısı gerçekten 90° olsaydı, üçüncü açının ölçüsü kaç derece olurdu ve bu durum neden bir üçgen oluşturmazdı?
16:21:49
Öğrenci
Cevabım: Üçgen üç acılı olduğu için bu yanlıştır çünkü eğer 90 + 90 yaparsak 180 olur ve üçüncü Açığa yer kalmaz veya 90 derecelik bir üçgen oluşturmaya çalışıyorsa aslı 45 45 ve 90 yapabilir
16:21:49
💭 AI Öğretmen
Hemen Bakıyorum
16:21:56
AI Öğretmen
Cevabınız tam olarak doğru değil, çünkü Aslı'nın iddiasının neden yanlış olduğunu tam açıklamamışsınız.
16:21:58
AI Öğretmen
Bir üçgenin iç açılarının toplamı her zaman 180°'dir. Eğer iki açısı 90° olsaydı, bu iki açı toplamda 180° yapar ve üçüncü açıya hiç yer kalmaz. Üçüncü açı 0° olursa, bu açıyla kapalı ve üç kenarlı bir şekil oluşturmak mümkün olmaz.
16:22:02
AI Öğretmen
Burada karışıklık olmuş gibi görünüyor; 45°, 45° ve 90° açılar bir dik üçgen oluşturur ama bu sadece bir açının 90° olabileceği durumdur. Soruda ise iki açının 90° olması isteniyor, bu ise mümkün değildir.
16:22:05
AI Öğretmen
Örnek vermek gerekirse, 90° + 90° = 180°, 180° - 180° = 0° üçüncü açı olur ki bu açı üçgen oluşturmaz. Bu yüzden Aslı'nın iddiası geometrik olarak yanlıştır.
16:22:06
AI Öğretmen
Bu nedenle doğru cevap, iki açısı 90° olan bir üçgenin mümkün olmadığıdır; üçüncü açı 0° olur ve bu bir üçgen oluşturmaz.
16:22:09
AI Öğretmen
Derse devam edelim mi?
16:23:02
Öğrenci
Olur, devam edelim
16:23:03
💭 AI Öğretmen
Güzel, devam edelim
16:23:13
AI Öğretmen
Dar açılı üçgen, üçgenlerin açılarına göre sınıflandırılmasından biridir.
16:23:13
AI Öğretmen
Bir üçgenin üç köşesindeki açının da 90 dereceden küçük olması gerekir.
16:23:14
AI Öğretmen
Bu tür üçgenlerde her bir köşe sivri ve dardır.
16:23:20
AI Öğretmen
Dar açılı üçgende hiçbir köşe 90 dereceye eşit veya 90 dereceden büyük olamaz.
16:23:22
AI Öğretmen
Bir üçgenin dar açılı olması için sadece bir veya iki köşesinin dar olması yetmez, tüm köşelerin dar açı olması gereklidir.
16:23:24
AI Öğretmen
Eğer üçgenin iki açısı dar ama bir açısı 90 dereceyse bu üçgen dar açılı değil, dik üçgendir.
16:23:26
AI Öğretmen
Sonuç olarak dar açılı üçgen, bütün açıları 90 dereceden küçük olan ve köşeleri sıkışmış gibi duran bir üçgendir.
16:23:28
AI Öğretmen
Dar açılı üçgenler hakkında anlattıklarımı anladınız mı?
16:23:58
Öğrenci
Anladım
16:24:02
💭 AI Öğretmen
Güzel, devam edelim
16:24:02
❓ Soru medium
Bir üçgenin iç açılarından ikisinin ölçüsü 55° ve 65°'dir. Bu üçgenin açılarına göre türünü belirleyiniz ve nedenini açıklayınız.
16:27:15
Öğrenci
Cevabım: 55+65=120 180-120=60. Bu bir danış açılır üçgenleri çünkü hiçbir ölçüsü 90°'yi geçmiyor.
16:27:15
💭 AI Öğretmen
Hemen Bakıyorum
16:27:22
AI Öğretmen
Harika bir iş çıkardın! Cevabın tamamen doğru ve adımların çok net.
16:27:24
AI Öğretmen
Üçgenin iç açılarının toplamının 180° olduğunu çok güzel kullandın ve üçüncü açıyı doğru bir şekilde 60° olarak buldun.
16:27:26
AI Öğretmen
Tüm açıların (55°, 65°, 60°) 90°'den küçük olduğunu fark etmen, bu üçgenin neden dar açılı bir üçgen olduğunu anlamanın anahtarıdır.
16:27:27
AI Öğretmen
Açı türlerine göre üçgenleri sınıflandırma konusundaki bilgin gerçekten sağlam!
16:27:28
AI Öğretmen
Dolayısıyla doğru cevap dar açılı üçgendir.
16:27:28
AI Öğretmen
Derse devam edelim mi?
16:27:58
Öğrenci
Olur, devam edelim
16:28:00
💭 AI Öğretmen
Güzel, ilerleyelim
16:28:07
Görsel
Görsel
16:28:10
AI Öğretmen
Bir üçgende, eğer açılardan biri 90 dereceden büyükse bu üçgene geniş açılı üçgen denir.
16:28:11
AI Öğretmen
Geniş açı, ölçüsü 90 derece ile 180 derece arasında olan açıdır.
16:28:12
AI Öğretmen
Bu yüzden geniş açılı üçgenlerde, bir köşe diğerlerine göre daha yayvan yani daha geniş gözükür.
16:28:13
AI Öğretmen
Bir üçgenin iç açılarının toplamı her zaman 180 derecedir.
16:28:15
AI Öğretmen
Bu nedenle, bir üçgende iki tane geniş açı olamaz.
16:28:17
AI Öğretmen
Çünkü iki geniş açının toplamı zaten 180’i bulur ya da geçer, böylece üçüncü açıya yer kalmaz.
16:28:17
AI Öğretmen
Geniş açılı üçgenlerde sadece bir tane geniş açı olur, diğer iki açı ise dar açı olur.
16:28:18
AI Öğretmen
Yani geniş açılı bir üçgende tek bir geniş açı ve iki dar açı bulunur.
16:28:20
AI Öğretmen
Geniş açılı üçgenler, dar açılı ve dik üçgenlerle birlikte iç açılarına göre yapılan temel üçgen türlerinden biridir.
16:28:21
AI Öğretmen
Geniş açılı üçgenler hakkında anlattıklarımı anladın mı?
16:29:01
Öğrenci
Anladım
16:29:03
💭 AI Öğretmen
Hmm
16:29:04
❓ Soru medium
Bir KLM üçgeni geniş açılı bir üçgendir. Bu üçgenin en büyük açısının ölçüsü 110°'dir. Diğer iki açıdan birinin ölçüsü diğerinin 3 katından 10° fazla olduğuna göre, bu üçgenin en küçük açısı kaç derecedir?
16:31:35
Öğrenci
Bir ipucu verir misiniz hocam?
16:31:36
💭 AI Öğretmen
Bir bakalım
16:31:38
AI Öğretmen
Bir üçgenin iç açılarının toplamının ne kadar olduğunu hatırlıyor musun?
16:31:40
AI Öğretmen
Verilen en büyük açı 110° ise, diğer iki açının toplamı kaç derece olmalı?
16:31:40
AI Öğretmen
Diğer iki açıdan birini x olarak alırsak, diğerini nasıl ifade edebiliriz?
16:36:30
Öğrenci
Cevabım: 1. 2. 3 110. 43 27. 2ve3'ün toplamı 70 olmalı.3. en küçüktür
16:36:31
💭 AI Öğretmen
Hemen Bakıyorum
16:36:37
AI Öğretmen
Cevabın doğru değil, çünkü açıların ölçüleri verilen koşulu sağlamıyor.
16:36:39
AI Öğretmen
Bir üçgenin iç açılarının toplamı her zaman 180°'dir. Burada bir açı 110° olduğuna göre, diğer iki açının toplamı 180° - 110° = 70° olmalı.
16:36:40
AI Öğretmen
Diğer iki açıdan birinin ölçüsü, diğerinin 3 katından 10° fazla olduğuna göre, küçük açıyı x dersek, büyük açı 3x + 10 olur.
16:36:42
AI Öğretmen
Bu iki açının toplamı 70° olduğundan, denklemi kurarız: x + (3x + 10) = 70. Bu denklemi çözdüğümüzde x = 15° bulunur.
16:36:44
AI Öğretmen
Yani en küçük açı 15°, diğer açı ise 55° olur. Senin verdiğin 43° ve 27° açıları bu ilişkiyi sağlamadığı için doğru değil.
16:36:46
AI Öğretmen
Bu tür problemlerde verilen koşulları dikkatlice denkleme dökmek ve toplamın 180° olduğunu unutmamak önemli. Bu yüzden doğru cevap en küçük açı olarak 15° olmalıdır.
16:36:46
AI Öğretmen
Derse devam edelim mi?
16:37:36
Öğrenci
Olur, devam edelim
16:37:38
💭 AI Öğretmen
Güzel, ilerleyelim
16:37:50
AI Öğretmen
Bir üçgenle ilgili bilmemiz gereken en temel kural, üçgenin iç açılarının toplamının her zaman $180^\circ$ olmasıdır.
16:37:51
AI Öğretmen
Üçgenin çeşidi ne olursa olsun, ister dar açılı, ister dik açılı, ister geniş açılı olsun, iç açıların ölçüleri toplandığında mutlaka $180^\circ$ çıkar.
16:37:53
AI Öğretmen
Eğer bir üçgende iki iç açı ölçüsünü biliyorsak, önce bu iki açıyı toplarız, sonra $180^\circ$’den bu toplamı çıkararak üçüncü açıyı buluruz.
16:37:54
AI Öğretmen
Bir üçgende iç açıların türüne göre sınıflandırma yaparız: Eğer bir iç açı tam olarak $90^\circ$ ise bu üçgen dik üçgendir.
16:37:56
AI Öğretmen
Üç iç açının da ölçüsü $90^\circ$’den küçükse, böyle üçgenlere dar açılı üçgen denir.
16:37:57
AI Öğretmen
Eğer üçgenin bir iç açısı $90^\circ$’den büyükse, yani genişse, bu üçgene geniş açılı üçgen adı verilir.
16:37:59
AI Öğretmen
Ama hangi tür üçgen olursa olsun, hepsinde ortak olan özellik, iç açıların toplamının $180^\circ$ olmasıdır.
16:38:00
AI Öğretmen
Üçgenlerin iç açılarının toplamının neden her zaman 180 derece olduğunu anladın mı?
16:38:52
Öğrenci
Anladım
16:38:56
💭 AI Öğretmen
Güzel, devam edelim
16:38:56
❓ Soru medium
Bir ABC üçgeninde A açısının ölçüsü 62° ve B açısının ölçüsü 48°'dir. Ali, C açısının ölçüsünü bulmak için şu işlemi yapmıştır: Önce 62 ile 48'i toplayarak 110 bulmuş, sonra da 180'den 110'u çıkararak sonucu 80° olarak hesaplamıştır. Ancak Ali'nin çıkarma işleminde bir hata vardır. Ali'nin hatasını düzelterek C açısının doğru ölçüsünü bulunuz ve bu üçgenin açılarına göre türünü (dar açılı, dik açılı, geniş açılı) belirtiniz.
16:39:09
Öğrenci
Bir ipucu verir misiniz hocam?
16:39:10
💭 AI Öğretmen
Tabii, bakıyorum
16:39:13
AI Öğretmen
Ali, 180’den 110’u çıkarırken hangi işlemi yapmış olabilir?
16:39:14
AI Öğretmen
Üçgenin iç açılarının toplamı neden 180°’dir ve bu bilgi C açısını bulmada nasıl yardımcı olur?
16:39:16
AI Öğretmen
C açısının ölçüsünü bulduktan sonra, bu açının 90° ile ilişkisini nasıl değerlendirirsin?
16:42:30
Öğrenci
Cevabım: c=70 a=62 b=48. bu bir dar açılı üçgendir
16:42:30
💭 AI Öğretmen
Hemen Bakıyorum
16:42:37
AI Öğretmen
Harika bir iş çıkardın!
16:42:38
AI Öğretmen
C açısının ölçüsünü doğru bir şekilde 70° olarak buldun ve üçgenin dar açılı olduğunu da doğru belirledin.
16:42:41
AI Öğretmen
Bir üçgenin iç açılarının toplamının 180° olması kuralını ve tüm açıları 90°'den küçük olan üçgenlerin dar açılı olduğunu çok iyi anlamışsın!
16:42:43
AI Öğretmen
Cevabın tam isabet!
16:42:43
AI Öğretmen
Derse devam edelim mi?
16:43:01
Öğrenci
Olur, devam edelim
16:43:10
💭 AI Öğretmen
Hmm
16:43:18
Görsel
Görsel
16:43:20
AI Öğretmen
Geometrik inşa, şekillerin oluşturulmasında doğrudan sayı kullanılmadan, sadece belirli araçlarla çizim yapılan bir yöntemdir.
16:43:22
AI Öğretmen
Bu yöntemde, uzunluklar 5 cm ya da 7 cm gibi ölçülerle belirtilmez.
16:43:23
AI Öğretmen
Bunun yerine, verilen bir uzunluk, açı veya konum, kullanılan araçlar yardımıyla bir yerden başka bir yere taşınır veya yeniden üretilir.
16:43:25
AI Öğretmen
Geometrik inşa çalışmalarının asıl amacı, verilen kurallara uygun, doğru ve eksiksiz bir şekil oluşturmak için sadece çizim kurallarını dikkate almaktır.
16:43:26
AI Öğretmen
Bu tür çizimlerde iki ana araç kullanılır.
16:43:28
AI Öğretmen
Pergel, çember çizmek veya bir noktadan alınan uzunluğu başka bir noktaya taşımak için kullanılır.
16:43:29
AI Öğretmen
Pergelin bir kez ayarlanan açıklığı sabit tutularak, aynı büyüklükteki aralıklar tekrar tekrar işaretlenebilir.
16:43:31
AI Öğretmen
Ölçüsüz cetvel ise yalnızca doğru çizmek için kullanılır, üzerindeki sayılara bakılmaz; sadece iki noktayı düz bir çizgiyle birleştiririz.
16:43:33
AI Öğretmen
Böylece hem pergel hem cetvel birlikte kullanılarak, sayı kullanmadan, çizim ve çemberin özelliklerinden yararlanıp üçgen gibi geometrik şekiller inşa edilebilir.
16:43:35
AI Öğretmen
Geometrik inşanın püf noktası, çember ve doğruların kesiştiği yerlerden yeni noktalar bulmak ve bu sayede istenen üçgenleri oluşturabilmektir.
16:43:37
AI Öğretmen
Geometrik inşa yöntemini ve kullanılan araçları anladınız mı?
16:44:42
Öğrenci
Anladım
16:44:45
💭 AI Öğretmen
Güzel, devam edelim
16:44:45
❓ Soru medium
Bir matematik projesinde, Elif'in görevi sadece pergel ve ölçüsüz cetvel kullanarak bir üçgen çizmektir. Elif çizime başlarken ilk olarak cetvelin üzerindeki santimetre işaretlerini kullanarak 8 cm uzunluğunda bir doğru parçası çizer ve bunu üçgenin ilk kenarı olarak belirler. Elif'in bu ilk adımı, metinde anlatılan geometrik inşa kurallarına göre neden hatalıdır ve bu kenarı doğru bir şekilde çizmek için ne yapmalıydı?
16:45:36
Öğrenci
Bir ipucu verir misiniz hocam?
16:45:38
💭 AI Öğretmen
Bir bakalım şimdi
16:45:41
AI Öğretmen
Elif'in cetvel üzerindeki santimetre işaretlerini kullanması, geometrik inşa kurallarına neden aykırıdır sence?
16:45:42
AI Öğretmen
Pergel ve ölçüsüz cetvelin kullanım amacı nedir, bu araçların hangi özellikleri çizim sırasında önemli olur?
16:45:44
AI Öğretmen
Elif, 8 cm uzunluğunu cetvel üzerindeki işaretlerle ölçmek yerine hangi yöntemle bu uzunluğu başka bir yerde tekrar oluşturabilirdi?
16:47:49
Öğrenci
Bir ipucu verir misiniz hocam?
16:47:51
💭 AI Öğretmen
Birlikte bakalım
16:47:56
AI Öğretmen
Elif'in cetvel üzerindeki santimetre işaretlerini kullanması, geometrik inşanın hangi temel kuralını ihlal ediyor olabilir?
16:47:57
AI Öğretmen
Pergel ile bir uzunluğu başka bir yere taşımak için hangi adımları izlemek gerekir?
16:47:59
AI Öğretmen
Cetvel üzerindeki sayısal işaretler olmadan uzunlukları nasıl kopyalayabiliriz?
16:49:13
Öğrenci
Cevabım: anlamadım
16:49:14
💭 AI Öğretmen
Hemen Bakıyorum
16:49:17
AI Öğretmen
Cevabınız doğru değil, çünkü soruyu anlamadığınızı belirtmişsiniz, ancak bu durumda size neden yanlış olduğunu ve doğru cevabın ne olduğunu açıklayayım.
16:49:19
AI Öğretmen
Elif'in yaptığı hata, ölçüsüz cetvelin üzerindeki santimetre işaretlerini kullanarak uzunluk ölçmesi ve bunu doğrudan çizimde kullanmasıdır. Geometrik inşada cetvel, sadece düz çizgiler çizmek için kullanılır, ölçü almak için değil.
16:49:19
AI Öğretmen
Doğru yöntem, pergel kullanarak uzunluğu kopyalamaktır. Pergelin uçlarını referans doğru parçasının uçlarına yerleştirip aralığı sabit tutar, sonra bu aralığı bozmadan yeni bir noktaya taşıyıp yay çizersiniz. Böylece uzunluk sayısal ölçü olmadan da aktarılmış olur.
16:49:20
AI Öğretmen
Yanlış anlamanın sebebi, cetvelin ölçüm aracı olarak kullanılabileceği düşüncesi olabilir, ama geometrik inşada bu kural değildir. Örneğin, bir uzunluğu başka yere taşımak için cetvel üzerindeki santimetre yerine pergel kullanılır.
16:49:22
AI Öğretmen
Bu yüzden doğru cevap, Elif'in cetvel üzerindeki işaretleri kullanmaması, uzunluğu pergelle kopyalamasıdır; dolayısıyla doğru cevap budur.
16:49:22
AI Öğretmen
Derse devam edelim mi?
16:50:28
Öğrenci
Olur, devam edelim
16:50:30
💭 AI Öğretmen
Tamam, devam edelim
16:50:41
AI Öğretmen
İkizkenar üçgen, iki kenarı birbirine tamamen eşit olan bir üçgendir.
16:50:42
AI Öğretmen
İkizkenar üçgen yapmak için pergelin açıklığını hiç değiştirmeden iki tane aynı büyüklükte çember çizmek gerekir.
16:50:44
AI Öğretmen
Çemberleri çizerken, her birinin merkezi farklı olmalı ama yarıçapları yani büyüklükleri aynı olmalıdır ve iki çember de birbirini kesmelidir.
16:50:46
AI Öğretmen
Çemberlerin merkezleri ile üstteki kesişme noktası cetvelle birleştirilir ve böylece bir üçgen çizilmiş olur.
16:50:48
AI Öğretmen
Çemberlerin yarıçapları eşit olduğu için, merkezlerden kesişim noktasına giden iki uzunluk da eşit olur ve bunlar üçgenin iki kenarını oluşturur.
16:50:49
AI Öğretmen
Bu şekilde çizilen üçgenin iki kenarı eşit olduğundan, ortaya çıkan üçgen ikizkenar üçgendir.
16:50:49
AI Öğretmen
Anlattığım ikizkenar üçgenin nasıl inşa edildiği kısmını anladın mı?
16:51:31
Öğrenci
Anladım
16:51:34
💭 AI Öğretmen
Güzel, devam edelim
16:51:34
❓ Soru medium
Ayşe, bir ikizkenar üçgen çizmek için pergel ve cetvel kullanmak istiyor. Önce A merkezli bir çember, daha sonra pergelin açıklığını değiştirerek B merkezli ikinci bir çember çiziyor. Bu iki çemberin kesiştiği noktalardan birini C olarak isimlendiriyor ve A, B ile C noktalarını birleştirerek bir üçgen oluşturuyor. Oluşturduğu ABC üçgeninin [AC] ve [BC] kenar uzunluklarının farklı olduğunu fark ediyor. Ayşe'nin bu çizimde ikizkenar üçgen elde edememesinin sebebi nedir ve doğru sonucu alması için ne yapması gerekirdi?
16:54:27
Öğrenci
Cevabım: Bu bir çeşit kanal üçgendir Ayşe'nin doğru Sonucu alması için yarı çaplar ve çaplar aynı uzunlukta ve merkezlerden geçmeyecek bir şekilde Çember çizilmesi gerek ve tekrardan abc diye isimlendirir ve üçgen oluşturur
16:54:28
💭 AI Öğretmen
Hemen Bakıyorum
16:54:34
AI Öğretmen
Cevabınız doğru değil, çünkü Ayşe'nin hatasını tam olarak belirtmemişsiniz ve "kanal üçgen" gibi yanlış bir terim kullanmışsınız.
16:54:36
AI Öğretmen
Ayşe'nin hatası, pergelin açıklığını değiştirerek iki farklı yarıçapta çember çizmesidir. Bu yüzden [AC] ve [BC] kenarları eşit olmamış ve ikizkenar üçgen oluşmamıştır.
16:54:38
AI Öğretmen
İkizkenar üçgen elde etmek için, Ayşe pergelin açıklığını değiştirmeden, yani aynı yarıçapla iki çember çizmelidir. Böylece iki kenar eşit olur.
16:54:39
AI Öğretmen
Örnek olarak, bir çember çizip aynı yarıçapla başka bir çember çizdiğinizde, kesişim noktalarından oluşan üçgenin iki kenarı eşit olur.
16:54:40
AI Öğretmen
Bu yüzden doğru cevap, pergelin açıklığını değiştirmeden eş yarıçaplı iki çember çizmek ve ardından kesişim noktalarını birleştirmektir.
16:54:41
AI Öğretmen
Bu nedenle doğru cevap, Ayşe'nin pergelin açıklığını değiştirmeden, eşit yarıçaplı iki çember çizmesi gerektiğidir.
16:54:41
AI Öğretmen
Derse devam edelim mi?
16:55:31
Öğrenci
Olur, devam edelim
16:55:32
💭 AI Öğretmen
Güzel, ilerleyelim
16:55:46
Görsel
Görsel
16:55:48
AI Öğretmen
Eşkenar üçgenin bütün kenarları aynı uzunluktadır.
16:55:49
AI Öğretmen
Pergel ve cetvel kullanılarak bir eşkenar üçgen çizmek için, pergelin açıklığını değiştirmemek çok önemlidir.
16:55:51
AI Öğretmen
Öncelikle, pergel istenen genişlikte açılır ve iğnesi bir yere batırılarak bir çember çizilir, bu nokta üçgenin bir köşesi olan A noktası olur.
16:55:55
AI Öğretmen
Sonra, pergeli hiç kapatmadan ve genişliğini değiştirmeden, iğne bu ilk çemberin çevresindeki herhangi bir noktaya taşınır ve aynı açıklıkla ikinci bir çember çizilir.
16:55:56
AI Öğretmen
Bu durumda, ikinci çemberin merkezi, birinci çemberin üzerinde bir noktada yer alır.
16:55:57
AI Öğretmen
İki çemberin kesiştiği üst noktadan, çemberlerin merkezlerine doğru düz çizgiler çizildiğinde bir üçgen oluşur.
16:55:59
AI Öğretmen
Birinci ve ikinci kenar, çizilen çemberlerin yarıçapıdır, yani ikisi de pergel açıklığı kadar olur.
16:55:59
AI Öğretmen
Çember merkezleri arasındaki mesafe de yine pergel açıklığına eşit olur.
16:56:01
AI Öğretmen
Bu yüzden, üç kenarın da uzunluğu aynı olur ve bu üçgen tanımı gereği eşkenar üçgen olur.
16:56:02
AI Öğretmen
Bu kısmı anladın mı, yoksa açıklamamda bir yerde takıldın mı?
16:56:57
Öğrenci
Pergel açıklığı neden değişmemelidir?
16:57:01
💭 AI Öğretmen
Güzel bir nokta
16:57:03
AI Öğretmen
Pergel açıklığının değişmemesi çok önemlidir çünkü böylece çizilen çemberlerin yarıçapları eşit olur.
16:57:06
AI Öğretmen
Pergelin açıklığı sabit kalırsa, çizilen iki çemberin yarıçapları ve merkezler arası mesafe eşit olur.
16:57:07
AI Öğretmen
Bu da üçgenin tüm kenarlarının eşit uzunlukta olmasını sağlar ve böylece eşkenar üçgen elde edilir.
16:57:08
AI Öğretmen
Eğer pergel açıklığı değişirse, çemberlerin yarıçapları farklı olur ve üçgen eşkenar olmaz.
16:57:09
AI Öğretmen
Anladın mı bu açıklamayı?
16:57:35
Öğrenci
Anladım
16:57:38
💭 AI Öğretmen
Güzel, anladın
16:57:39
❓ Soru medium
Ayşe, bir eşkenar üçgen çizmek için pergelini 6 cm açarak A merkezli bir çember çiziyor. Daha sonra pergelin iğnesini, bu çember üzerindeki bir B noktasına koyuyor ve pergelin açıklığını yanlışlıkla 5 cm olacak şekilde değiştirerek B merkezli ikinci bir çember çiziyor. Bu iki çemberin kesiştiği C noktasını, A ve B noktalarıyla birleştirerek bir ABC üçgeni oluşturuyor. Ayşe'nin bu çizimde yaptığı hata nedir ve eğer hata yapmasaydı oluşturacağı doğru eşkenar üçgenin çevresi kaç santimetre olurdu?
16:58:25
Öğrenci
Bir ipucu verir misiniz hocam?
16:58:28
💭 AI Öğretmen
Hemen bakıyorum now
16:58:30
AI Öğretmen
Pergel açıklığının eşkenar üçgen çizimindeki rolü nedir sizce?
16:58:31
AI Öğretmen
İkinci çember çizilirken pergel açıklığının değiştirilmesinin üçgenin kenar uzunluklarına nasıl etkisi olabilir?
16:58:33
AI Öğretmen
Eğer pergel açıklığı sabit tutulursa üçgenin kenar uzunlukları nasıl olur ve bu da çevreyi nasıl etkiler?
16:58:54
Öğrenci
Bir ipucu verir misiniz hocam?
16:58:56
💭 AI Öğretmen
Bir bakalım şimdi
16:58:59
AI Öğretmen
Ayşe'nin çiziminde pergel açıklığını neden değiştirmemesi gerektiğini düşünürsek, bu değişikliğin üçgenin kenar uzunlukları üzerinde ne gibi bir etkisi olabilir?
16:59:00
AI Öğretmen
Eşkenar üçgenin tüm kenarlarının eşit olması gerektiğini hatırlarsak, pergel açıklığının sabit kalması bu eşitliği nasıl sağlar?
16:59:03
AI Öğretmen
Eğer pergel açıklığını değiştirmeden doğru şekilde çizseydi, üçgenin bir kenarının uzunluğu kaç cm olurdu ve bu durumda çevresi nasıl hesaplanırdı?
17:00:56
Öğrenci
şimdiki soruyu anlamadım
17:00:57
💭 AI Öğretmen
Maalesef.
17:00:58
AI Öğretmen
Daha fazla ipucu veremem. Lütfen soruyu cevaplamaya çalış.
17:30:58
Öğrenci
haydi derse devam edelim
17:30:58
💭 AI Öğretmen
Tamam, şimdi en son bu soruya bakıyorduk
17:30:58
❓ Soru medium
Ayşe, bir eşkenar üçgen çizmek için pergelini 6 cm açarak A merkezli bir çember çiziyor. Daha sonra pergelin iğnesini, bu çember üzerindeki bir B noktasına koyuyor ve pergelin açıklığını yanlışlıkla 5 cm olacak şekilde değiştirerek B merkezli ikinci bir çember çiziyor. Bu iki çemberin kesiştiği C noktasını, A ve B noktalarıyla birleştirerek bir ABC üçgeni oluşturuyor. Ayşe'nin bu çizimde yaptığı hata nedir ve eğer hata yapmasaydı oluşturacağı doğru eşkenar üçgenin çevresi kaç santimetre olurdu?
17:31:08
Öğrenci
Bir ipucu verir misiniz hocam?
17:31:08
💭 AI Öğretmen
Maalesef.
17:31:09
AI Öğretmen
Daha fazla ipucu veremem. Lütfen soruyu cevaplamaya çalış.
17:33:50
Öğrenci
Cevabım: önce çizdiği üçgen İle sonraki çizdiği üçgenin santimetresini eşit çizseydi kenarda bir üçgen olurdu tabi doğru yapsaydı yanlış yaptığı için de bu bir çeşit kenar veya ikizkenar üçgen olabilir
17:33:50
💭 AI Öğretmen
Hemen Bakıyorum
17:33:58
AI Öğretmen
Cevabınız tam olarak doğru değil, çünkü Ayşe'nin yaptığı hatayı ve doğru cevabın çevresini belirtmemişsiniz.
17:34:00
AI Öğretmen
Ayşe'nin yaptığı temel hata, pergel açıklığını ilk çizimdeki 6 cm'den sonra 5 cm'ye düşürmesidir. Eşkenar üçgen çizmek için pergel açıklığı sabit kalmalıdır.
17:34:02
AI Öğretmen
Eğer pergel açıklığı hep 6 cm olsaydı, üçgenin tüm kenarları 6 cm olurdu ve çevresi 3 x 6 = 18 cm olurdu.
17:34:04
AI Öğretmen
Bu yüzden, doğru eşkenar üçgenin çevresi 18 cm'dir. Siz kenar uzunluklarını ve çevreyi belirtmediğiniz için cevabınız eksik kalmış.
17:34:05
AI Öğretmen
Doğru cevap, Ayşe'nin pergel açıklığını değiştirmemesi ve üçgenin çevresinin 18 cm olmasıdır.
17:34:05
AI Öğretmen
Derse devam edelim mi?
17:37:17
Öğrenci
Olur, devam edelim
17:37:20
💭 AI Öğretmen
Hmm
17:37:29
AI Öğretmen
Üçgen çiziminde, pergelle yapılan işlemlerde pergelin açıklığının aynı kalması çok önemlidir.
17:37:30
AI Öğretmen
Eğer ikinci bir çember çizerken pergelin açıklığını değiştirirsek, ikinci çemberin yarıçapı farklı olur ve üçgenin kenarları eşit çıkmaz.
17:37:31
AI Öğretmen
Bu yüzden üçgeni doğru bir şekilde inşa edemeyiz.
17:37:34
AI Öğretmen
Geometri sorularında sıkça geçen “ölçüsüz cetvel” ifadesi de önemlidir çünkü bu cetvelin üzerinde sayılar, ölçü birimleri dikkate alınmaz.
17:37:35
AI Öğretmen
Cetvel sadece düz bir doğru çizmek için kullanılır, cetvelin üstündeki işaretlere veya numaralara bakılmaz.
17:37:36
AI Öğretmen
Yani çizim yaparken kenarların uzunluğu ölçülmez, sadece doğruların kendisi çizilir.
17:37:37
AI Öğretmen
Üçgen oluştururken de çizgiler rastgele noktalardan geçmemelidir.
17:37:40
AI Öğretmen
Çizgiler, pergelin iğnesinin bıraktığı merkez noktalar ve çemberlerin kesişim noktalarından geçirilmelidir.
17:37:42
AI Öğretmen
Pergelin açıklığı hiç değişmediğinde, yapılan tüm yaylar ve çemberlerin yarıçapları birbirine eşit olur.
17:37:43
AI Öğretmen
Böylece, bu merkezler ve kesişim noktaları doğru şekilde birleştirildiğinde hedeflenen özellikte üçgenler oluşturulur.
17:37:44
AI Öğretmen
Bu kısmı anladın mı, yoksa açıklamamı istediğin bir yer var mı?
17:38:37
Öğrenci
Anladım
17:38:42
💭 AI Öğretmen
Hmm
17:38:43
❓ Soru medium
Elif, bir eşkenar üçgen çizmek için pergel ve cetvel kullanıyor. Önce 8 cm uzunluğunda bir AB doğru parçası çiziyor. Sonra pergelini 8 cm açıp sivri ucunu A noktasına koyarak bir yay çiziyor. Bu adımdan sonra, pergelin açıklığını yanlışlıkla 7 cm'e düşürüyor ve sivri ucunu B noktasına koyarak ilk yayı kesen ikinci bir yay çiziyor. Yayların kesişim noktasını C olarak adlandırıp A, B ve C noktalarını birleştiriyor. Elif'in yaptığı hata nedir ve bu hatanın sonucunda ortaya çıkan ABC üçgeni, kenar uzunluklarına göre nasıl bir üçgendir?

Voltran Okul Analiz Sistemi