← Ana Rapor / ÖMER METE PULAT / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
25 October 2025, 12:54
Bitiş
Devam ediyor
Süre
23 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Çarpanlar Ve Katlar
Alt Konular:
  • Pozitif Tam Sayıların Pozitif Tam Sayı Çarpanları
Kazanımlar:
  • Verilen pozitif tam sayıların pozitif tam sayı çarpanlarını bulur, pozitif tam sayıların pozitif tam sayı çarpanlarını üslü ifadelerin çarpımı şeklinde yazar.

Detaylı Değerlendirme

Öğrenci Performans Analizi

Bu ders seansında öğrencinin "Çarpanlar ve Katlar" konusundaki performansı karma bir tablo çizmiştir. Öğrenci, bir sayının pozitif tam sayı çarpanlarını bularak temel problemleri çözme konusunda başarılı olurken, konunun daha karmaşık ve soyut kısımlarında belirgin zorluklar yaşamıştır.

# Başarılı Olduğu Konular
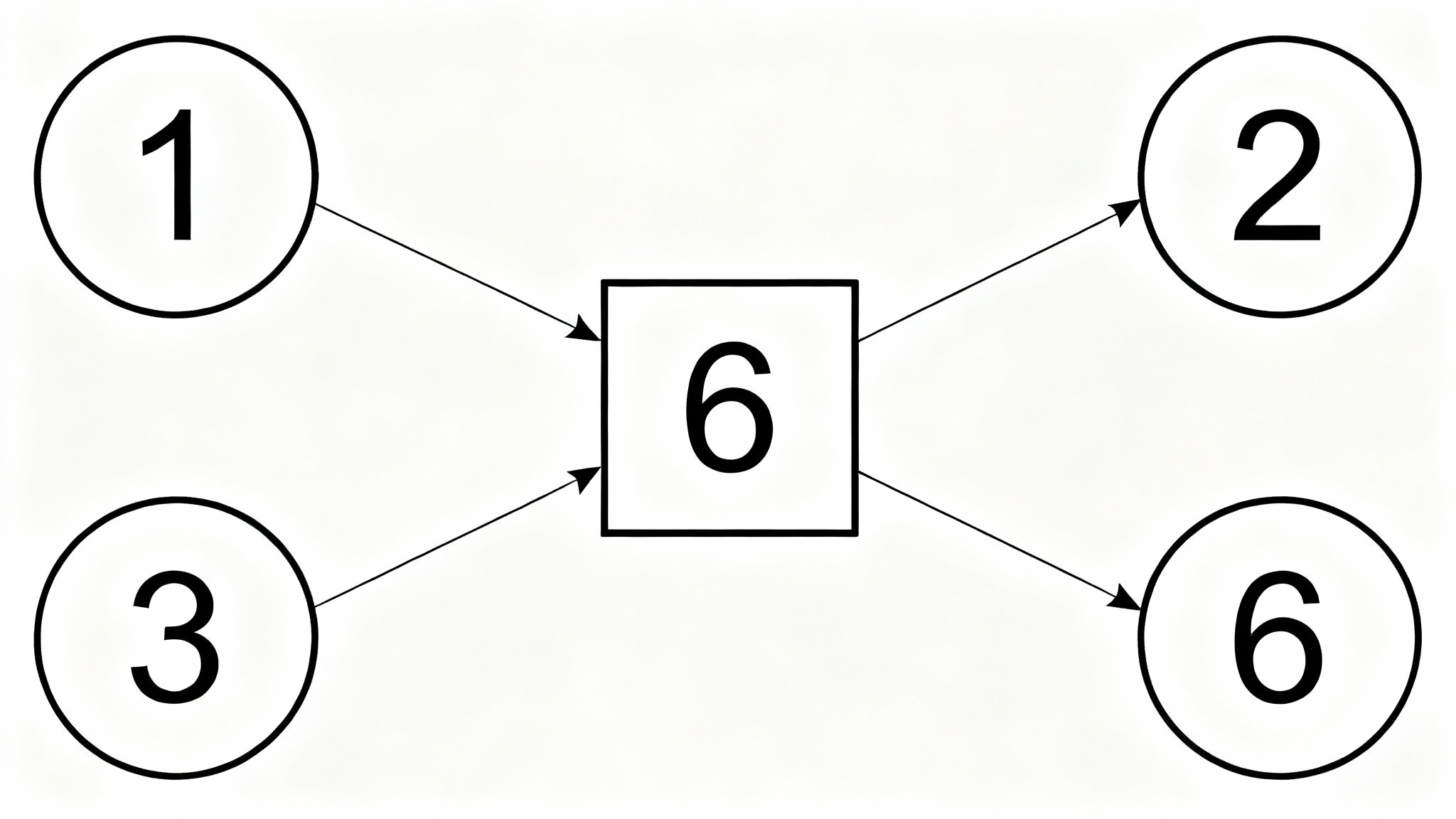
Öğrenci, bir sayının pozitif tam sayı çarpanlarını (bölenlerini) listeleyerek bu bilgiyi problem çözümünde kullanma konusunda yetkinlik göstermiştir. Özellikle, alanı verilen bir dikdörtgenin olası çevre uzunluklarını hesaplamayı gerektiren iki soruyu da doğru yanıtlamıştır. Bu, öğrencinin somut örnekler üzerinden çarpan bulma ve bu çarpanları geometrik problemlerle ilişkilendirme becerisinin iyi olduğunu göstermektedir.

- Örnek: Alanı 72 cm² ve 120 cm² olan dikdörtgenlerin çevreleriyle ilgili soruları doğru çözmesi.

# Geliştirilmesi Gereken Konular
Öğrencinin en belirgin eksiği, pozitif tam sayı çarpanlarının sayısını bulma ve asal çarpanlar algoritması (bölen listesi) konularında ortaya çıkmıştır.
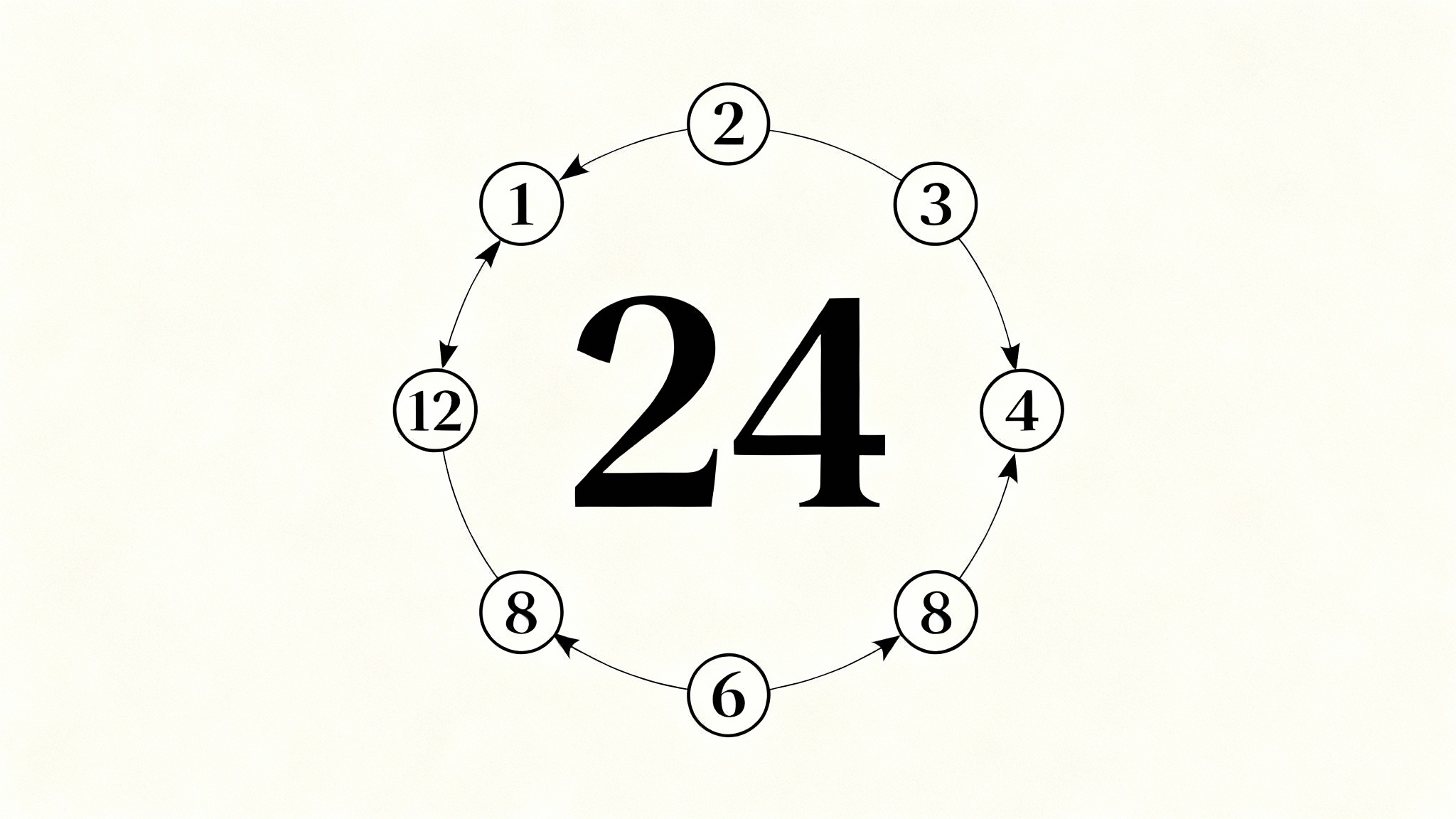
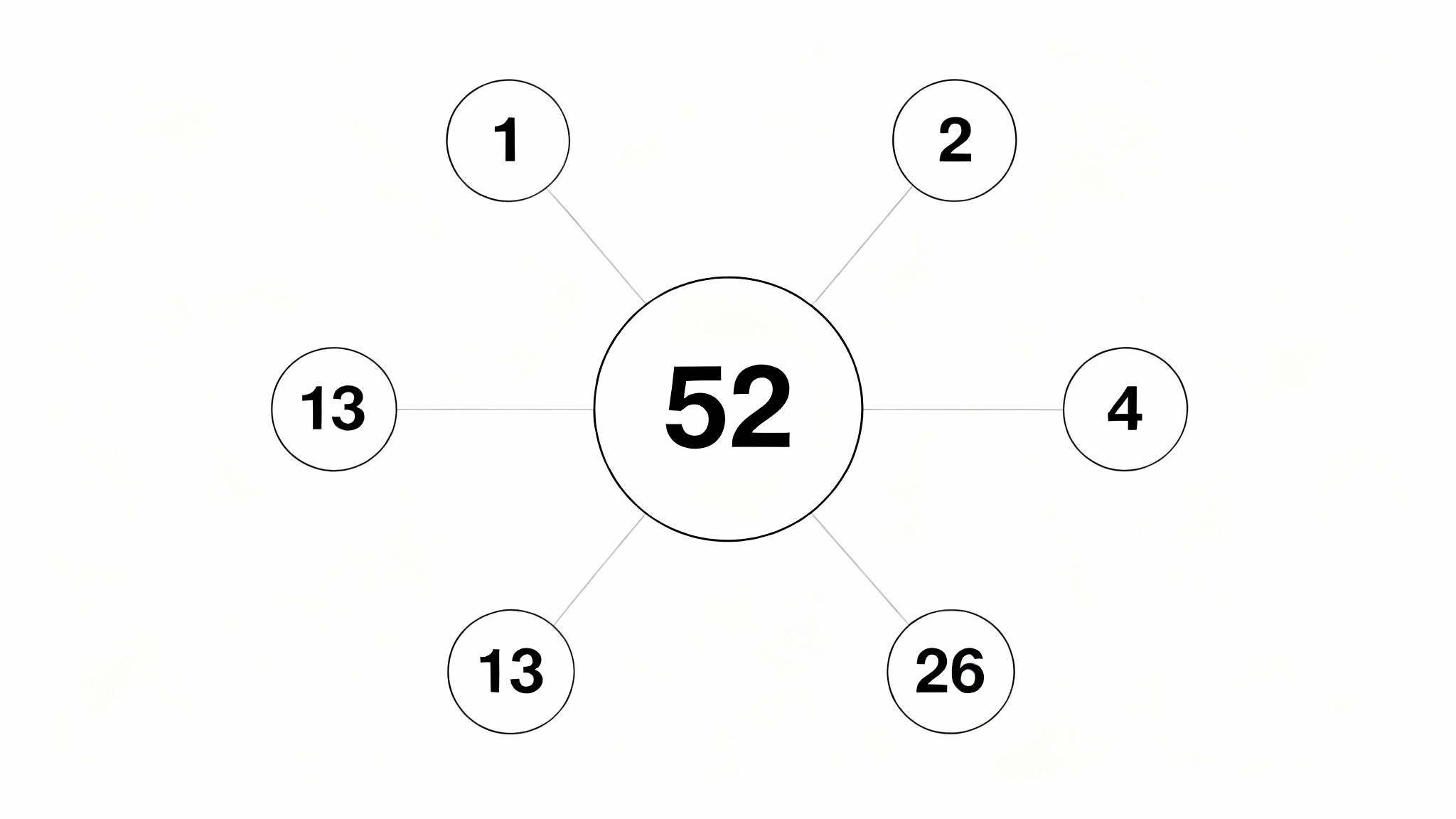
- Çarpan Sayısı Formülü: Pozitif çarpan sayısı verilen bir sayının kendisini bulmayı gerektiren ilk soruda, öğrenci iki kez ipucu istemesine rağmen çözüme ulaşamamış ve "bulamadım" yanıtını vermiştir. Bu durum, sayıyı asal çarpanların üslü çarpımı şeklinde yazma ve üsleri kullanarak çarpan sayısını bulma formülünü anlamakta zorlandığını göstermektedir.
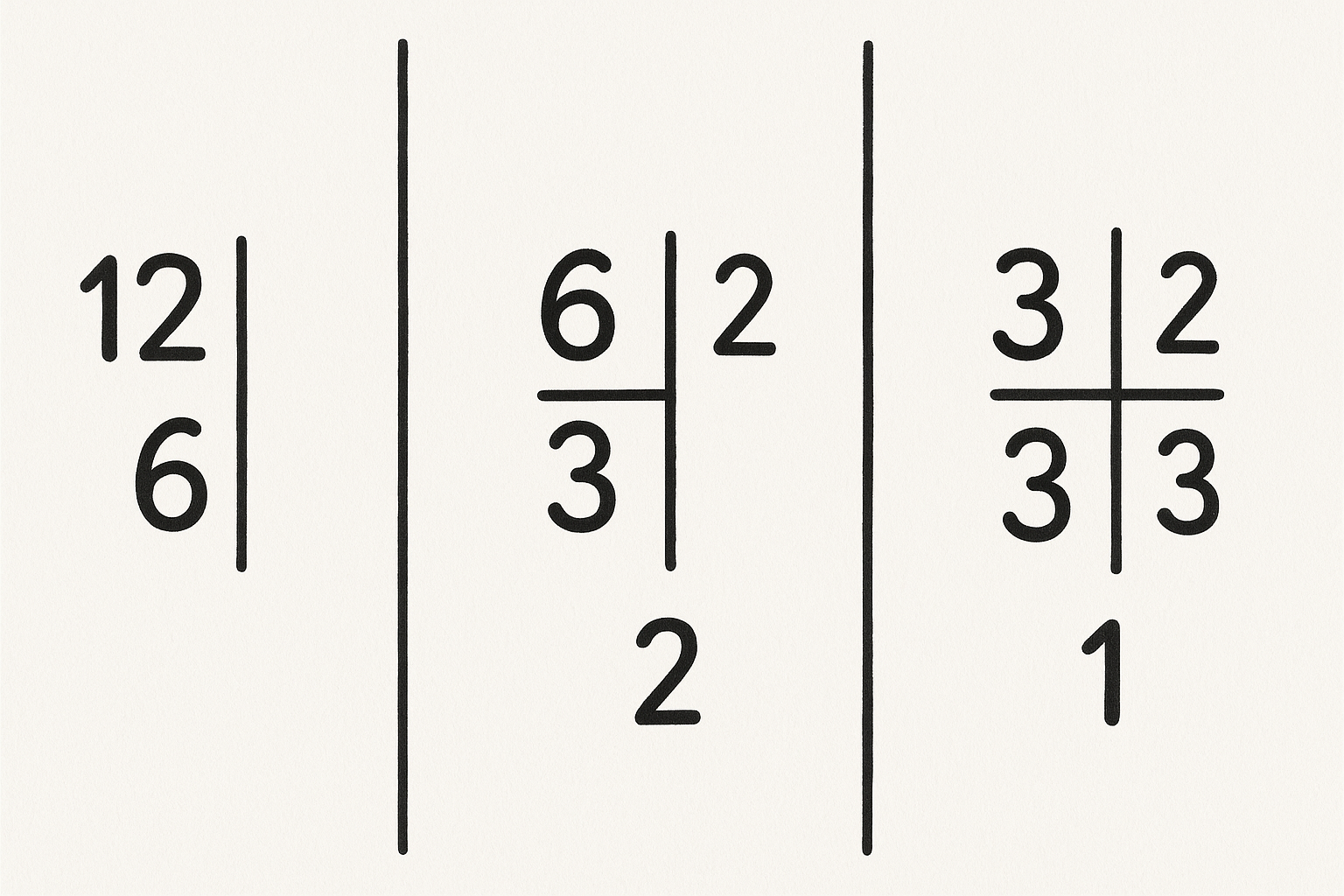
- Asal Çarpanlara Ayırma: Öğretmen, "bölen listesi" yöntemini kullanarak bir sayıyı asal çarpanlarına ayırmayı anlattığında, öğrenci "Biraz daha yavaş anlatır mısınız?" diyerek konuyu takip etmekte zorlandığını belirtmiştir. Bu, asal çarpanlara ayırma yönteminin temel mantığını kavramada güçlük çektiğine işaret etmektedir.

# Özet
Öğrenci, "çarpan" kavramını temel düzeyde anlamış ve basit problem türlerinde uygulayabilmektedir. Ancak, konunun temelini oluşturan asal çarpanlara ayırma ve bunun uygulamaları (çarpan sayısı bulma gibi) konusunda ciddi eksiklikleri bulunmaktadır. Öğrencinin bu konulardaki temelini sağlamlaştırması, ilerleyen konularda (EBOB-EKOK vb.) başarılı olması için kritik öneme sahiptir.

📜 Oturum Detayları

12:54:31
Öğrenci
Evet, hazırım Hocam! Bu konuyu detaylıca anlatır mısın?
12:54:32
💭 AI Öğretmen
Hemen başlıyoruz
12:54:32
Görsel
Görsel
12:54:35
AI Öğretmen
Her doğal sayı, iki doğal sayının çarpılmasıyla elde edilebilir.
12:54:36
AI Öğretmen
Bu şekilde çarpılan iki sayıya, o doğal sayının çarpanları denir.
12:54:37
AI Öğretmen
Bir doğal sayının pozitif tam sayı çarpanları, o sayıyı kalansız yani tam bölebilen pozitif tam sayılardır.
12:54:38
AI Öğretmen
Başka bir deyişle, pozitif tam sayı çarpanları aynı zamanda o sayının bölenleridir.
12:54:38
AI Öğretmen
Çarpanlar konusu, bir sayının hangi sayılara tam bölünebildiğini bulmamıza yardımcı olur.
12:54:40
AI Öğretmen
Örneğin, 6 sayısının çarpanları 1, 2, 3 ve 6’dır.
12:54:41
AI Öğretmen
Bu sayılar, 6’yı kalansız bölebilen pozitif tam sayılardır.
12:54:42
AI Öğretmen
Pozitif tam sayıların çarpanlarını bulmak da çarpanlar ve katlar konusunun temelini oluşturur.
12:54:43
AI Öğretmen
Çarpanlar konusu ile ilgili anlattıklarımı anladın mı?
12:55:15
Öğrenci
Anladım
12:55:16
💭 AI Öğretmen
Şimdi konuyu pekiştirelim
12:55:17
❓ Soru medium
$A$ pozitif tam sayısının pozitif tam sayı çarpanlarının sayısı $15$'tir. $A \lt 500$ olduğuna göre, $A$'nın alabileceği tüm değerlerin toplamı kaçtır?
12:55:54
Öğrenci
Bir ipucu verir misiniz hocam?
12:55:55
💭 AI Öğretmen
Bir düşünelim hemen
12:55:57
AI Öğretmen
Pozitif tam sayıların çarpan sayısını bulmak için sayının asal çarpanlarına ayrılması gerektiğini biliyor musun?
12:55:58
AI Öğretmen
Çarpan sayısı formülünde üslerin ne şekilde kullanıldığını hatırlıyor musun?
12:55:59
AI Öğretmen
Çarpan sayısı 15 olduğunda, bu sayıyı hangi çarpanların çarpımı olarak yazabilirsin?
12:59:31
Öğrenci
Bir ipucu verir misiniz hocam?
12:59:32
💭 AI Öğretmen
Bir bakalım
12:59:34
AI Öğretmen
Bir sayının pozitif tam sayı çarpanlarının sayısını bulmak için sayı hangi şekilde ifade edilir?
12:59:35
AI Öğretmen
Asal çarpanlara ayrılmış bir sayının çarpan sayısını bulmak için hangi formülü kullanırız?
12:59:36
AI Öğretmen
Çarpan sayısı 15 olan bir sayının asal çarpanlarının üsleri nasıl olabilir?
13:06:02
Öğrenci
Cevabım: bulamadım
13:06:02
💭 AI Öğretmen
Hemen Bakıyorum
13:06:08
AI Öğretmen
Cevabınız doğru değil, çünkü sorunun çözümünü bulamadığınızı belirtmişsiniz. Endişelenmeyin, birlikte adım adım açıklayalım.
13:06:10
AI Öğretmen
Bir sayının pozitif tam sayı çarpanlarının sayısını bulmak için sayıyı asal çarpanlarına ayırırız. Eğer sayı \(A = x^a \cdot y^b \cdot z^c \cdot ...\) şeklindeyse, çarpan sayısı \((a+1)(b+1)(c+1)...\) formülüyle hesaplanır.
13:06:14
AI Öğretmen
Soruda çarpan sayısı 15 olarak verilmiş. 15 sayısını çarpanlarına ayırdığımızda, ya tek bir asal sayının kuvveti olarak \((a+1) = 15\) ya da iki asal sayının kuvvetlerinin çarpımı olarak \((a+1)(b+1) = 15\) olabilir.
13:06:16
AI Öğretmen
İlk durumda \(a = 14\) olur ve sayı \(x^{14}\) şeklindedir. En küçük asal sayı 2 olduğunda \(2^{14} = 16384\) olur ki bu 500’den büyüktür, bu yüzden bu durum geçerli değildir.
13:06:20
AI Öğretmen
İkinci durumda ise 15’i 3 ve 5 olarak ayırabiliriz: \((a+1) = 3\) ve \((b+1) = 5\) veya tam tersi. Yani \(a=2\), \(b=4\) veya \(a=4\), \(b=2\) olur.
13:06:22
AI Öğretmen
Şimdi \(A = x^4 \cdot y^2\) veya \(A = x^2 \cdot y^4\) şeklinde sayılar arıyoruz. En küçük asal sayılarla deneyelim:
13:06:25
AI Öğretmen
- \(2^4 \cdot 3^2 = 16 \cdot 9 = 144 < 500\)
13:06:27
AI Öğretmen
- \(3^4 \cdot 2^2 = 81 \cdot 4 = 324 < 500\)
13:06:31
AI Öğretmen
- \(2^4 \cdot 5^2 = 16 \cdot 25 = 400 < 500\)
13:06:33
AI Öğretmen
- \(5^4 \cdot 2^2 = 625 \cdot 4 = 2500 > 500\) (geçerli değil)
13:06:36
AI Öğretmen
Böylece \(A\) sayısının alabileceği değerler 144, 324 ve 400’dür.
13:06:37
AI Öğretmen
Bu sayıların toplamı \(144 + 324 + 400 = 868\) olur.
13:06:39
AI Öğretmen
Sonuç olarak, doğru cevap 868’dir. Soru zor görünebilir ama bu yöntemle adım adım ilerlemek çözümü kolaylaştırır.
13:06:39
AI Öğretmen
Derse devam edelim mi?
13:08:08
Öğrenci
Olur, devam edelim
13:08:09
💭 AI Öğretmen
Devam ediyoruz hemen
13:08:14
Görsel
Görsel
13:08:17
AI Öğretmen
Bir sayının çarpanları, o sayıyı tam olarak bölen yani bölüm yaptığımızda kalan sıfır olan pozitif tam sayılardır.
13:08:18
AI Öğretmen
24 sayısının çarpanlarını bulmak için, hangi sayıların 24’ü kalansız böldüğüne bakarız.
13:08:19
AI Öğretmen
Çarpan çiftlerini araştırdığımızda şöyle sıralayabiliriz: 1 × 24, 2 × 12, 3 × 8, 4 × 6.
13:08:21
AI Öğretmen
Bu çiftlerde yer alan tüm sayılar, 24’ü böler ve bu yüzden çarpanlardır.
13:08:23
AI Öğretmen
Yani, 24’ü kalansız bölen pozitif tam sayılar şunlardır: 1, 2, 3, 4, 6, 8, 12 ve 24.
13:08:24
AI Öğretmen
Bu sayılardan biriyle başka bir çarpanı çarptığımızda sonuç daima 24 olur.
13:08:25
AI Öğretmen
Örneğin, 2 × 12 = 24 olduğu için hem 2 hem de 12, 24’ün çarpanlarıdır.
13:08:28
AI Öğretmen
Aynı şekilde, 3 × 8 = 24 ve 4 × 6 = 24 işlemlerini incelediğimizde diğer çarpanları da görebiliriz.
13:08:30
AI Öğretmen
Sonuç olarak 24’ü kalansız bölebilen pozitif tam sayılar şunlardır: 1, 2, 3, 4, 6, 8, 12 ve 24.
13:08:31
AI Öğretmen
24 sayısının çarpanlarını bulma konusunu anladın mı?
13:09:21
Öğrenci
Anladım
13:09:22
💭 AI Öğretmen
Şimdi soruya geçelim
13:09:23
❓ Soru medium
Alanı $72$ cm$^2$ olan bir dikdörtgenin kenar uzunlukları, santimetre cinsinden $1$'den büyük birer tam sayıdır. Bu dikdörtgenin çevre uzunluğunun alabileceği kaç farklı tam sayı değeri vardır?
13:11:11
Öğrenci
Cevabım: 5
13:11:12
💭 AI Öğretmen
Hemen Bakıyorum
13:11:15
AI Öğretmen
Harika bir iş çıkardın! Cevabın kesinlikle doğru!
13:11:16
AI Öğretmen
Alanı 72 cm² olan bir dikdörtgenin kenar uzunlukları için 72'nin 1'den büyük tüm çarpan çiftlerini bulman, soruyu çözmenin anahtarıydı.
13:11:17
AI Öğretmen
Bu çarpan çiftlerini bulduktan sonra, her bir çift için çevre uzunluğunu doğru bir şekilde hesaplayarak farklı değerleri belirledin.
13:11:18
AI Öğretmen
Bu tür sorularda tüm olası durumları gözden geçirmek ve her bir durum için istenen değeri hesaplamak çok önemlidir. Tebrikler!
13:11:19
AI Öğretmen
Doğru cevap 5'tir.
13:11:19
AI Öğretmen
Derse devam edelim mi?
13:11:48
Öğrenci
Olur, devam edelim
13:11:48
💭 AI Öğretmen
Devam edelim şimdi
13:12:01
Görsel
Görsel
13:12:04
AI Öğretmen
Bir sayının pozitif tam sayı çarpanlarını bulmak için, 1’den başlayarak o sayıyı kalansız bölen tüm tam sayılar seçilir.
13:12:06
AI Öğretmen
Şimdi 52 sayısının çarpanlarını adım adım bulalım.
13:12:07
AI Öğretmen
İlk adımda $52 \div 1 = 52$ olduğunda, 1 ve 52 çarpan olur.
13:12:09
AI Öğretmen
$52 \div 2 = 26$ işlemiyle de 2 ve 26 çarpan yapar.
13:12:10
AI Öğretmen
$52$ sayısı 3’e tam bölünmediği için, 3 çarpan değildir.
13:12:11
AI Öğretmen
$52 \div 4 = 13$ işlemiyle 4 ve 13 de çarpan olur.
13:12:13
AI Öğretmen
52; 5, 6 ve 7’ye bölünmez, yani bu sayılar çarpan değildir.
13:12:14
AI Öğretmen
Bunlar dışında kalan başka bir çarpan yoktur.
13:12:16
AI Öğretmen
Sonuç olarak, 52 sayısının pozitif tam sayı çarpanları 1, 2, 4, 13, 26 ve 52’dir.
13:12:17
AI Öğretmen
Ayrıca, pratik olarak, kontrol ederken sadece $\sqrt{52}$ yani yaklaşık 7,2’ye kadar olan sayılara bakarsak diğer tüm çarpanları da bulabiliriz.
13:12:19
AI Öğretmen
52 sayısının çarpanlarını bulma yöntemini anladın mı?
13:13:00
Öğrenci
Anladım
13:13:02
💭 AI Öğretmen
Şimdi bir soru gelecek
13:13:03
❓ Soru medium
Kenar uzunlukları santimetre cinsinden birer pozitif tam sayı olan bir dikdörtgenin alanı $144 \text{ cm}^2$'dir. Bu bilgilere göre, bu dikdörtgenin çevre uzunluğunun alabileceği en büyük değer ile en küçük değerin farkı kaç santimetredir?
13:14:39
Öğrenci
Cevabım: 242
13:14:40
💭 AI Öğretmen
Hemen Bakıyorum
13:14:45
AI Öğretmen
Harika bir iş çıkardın! Cevabın kesinlikle doğru!
13:14:45
AI Öğretmen
Dikdörtgenin alanını kullanarak kenar uzunluklarının çarpanlarını doğru bir şekilde belirledin ve bu çarpanlar arasından çevreyi en büyük ve en küçük yapanları buldun.
13:14:47
AI Öğretmen
Burada önemli olan, kenar uzunlukları arasındaki fark büyüdükçe çevrenin de büyümesi ve kenarlar birbirine yaklaştıkça çevrenin küçülmesidir.
13:14:49
AI Öğretmen
Bu tür problemler, çarpanları ve geometrik şekillerin özelliklerini anlamak için çok faydalıdır.
13:14:49
AI Öğretmen
Doğru cevap 242.
13:14:49
AI Öğretmen
Derse devam edelim mi?
13:15:14
Öğrenci
Olur, devam edelim
13:15:15
💭 AI Öğretmen
Tamam, hemen ilerliyoruz
13:15:24
Görsel
Görsel
13:15:26
AI Öğretmen
Bir sayının pozitif tam sayı çarpanları vardır ve bu çarpanlardan yalnızca kendisi ve 1'e bölünebilenlere asal sayı denir.
13:15:28
AI Öğretmen
Yani bir sayının asal çarpanları dediğimizde, o sayının kendisi dışında pozitif olarak bölen asal sayıları kastediyoruz.
13:15:29
AI Öğretmen
Asal çarpanlar, verilen sayıyı hiç kalan olmadan bölebilen asal sayılardır.
13:15:30
AI Öğretmen
Bir sayının asal çarpanlarını bulmak için en çok kullanılan yöntemlerden biri bölen listesi yöntemidir.
13:15:35
AI Öğretmen
Bölen listesi yöntemini uygularken, önce asal çarpanlarına ayırmak istediğimiz sayıyı yazar ve hemen yanına dik bir çizgi çizeriz.
13:15:37
AI Öğretmen
Daha sonra, bu sayıyı kalansız bölen en küçük asal sayıyı çizginin sağına yazarız ve bölme işlemini başlatırız.
13:15:38
AI Öğretmen
Elde ettiğimiz sonucu çizginin solundaki sayının altına yazarız.
13:15:39
AI Öğretmen
Bu işlemi, sonuç 1 olana kadar devam ettiririz, her seferinde asal sayılarla böleriz.
13:15:39
AI Öğretmen
Çizginin sağına yazdığımız asal sayılar, o sayının asal çarpanlarıdır.
13:15:41
AI Öğretmen
Şimdi, 12 sayısını örnek olarak bölen listesi yöntemiyle asal çarpanlarına ayıralım.
13:15:42
AI Öğretmen
Önce 12'nin yanına dik çizgimizi çekiyoruz ve en küçük asal sayı 2 ile bölüyoruz:
13:15:43
AI Öğretmen
12 | 2 → 6
13:15:44
AI Öğretmen
Sonra, 6'yı tekrar 2 ile böleriz:
13:15:45
AI Öğretmen
6 | 2 → 3
13:15:46
AI Öğretmen
3 ise asal bir sayı olduğu için 3 ile böleriz:
13:15:46
AI Öğretmen
3 | 3 → 1
13:15:47
AI Öğretmen
En son sonuç 1 olduğu için duruyoruz.
13:15:49
AI Öğretmen
Sonuç olarak, 12'nin asal çarpanları 2, 2 ve 3'tür. Yani 12 = 2·2·3 şeklinde yazılır.
13:15:50
AI Öğretmen
Bölen listesi yöntemiyle asal çarpanları bulma kısmını anladın mı?
13:17:12
Öğrenci
Biraz daha yavas anlatirmisiniz
13:17:17
💭 AI Öğretmen
Tabii, biraz daha açıklayayım
13:17:20
AI Öğretmen
Tabii, daha yavaş ve adım adım anlatalım. Öncelikle 12 sayısını ele alalım.
13:17:21
AI Öğretmen
12 sayısını yazıyoruz ve yanına kalansız bölebildiğimiz en küçük asal sayı olan 2’yi yazıyoruz.
13:17:23
AI Öğretmen
Sonra 12’yi 2’ye bölüyoruz, sonuç 6 oluyor. 6’yı da tekrar 2’ye bölüyoruz, sonuç 3 oluyor.
13:17:24
AI Öğretmen
Son olarak 3’ü kendisine bölüyoruz, sonuç 1 oluyor ve işlem burada bitiyor.
13:17:26
AI Öğretmen
Yan tarafta yazdığımız asal sayılar 2, 2 ve 3’tür. Bunlar 12’nin asal çarpanlarıdır.
13:17:27
AI Öğretmen
Yani 12 = 2 × 2 × 3 şeklinde yazılır.
13:17:29
AI Öğretmen
Böylece bir sayının asal çarpanlarını bulmuş oluyoruz.
13:17:29
AI Öğretmen
Bu anlatımı anladın mı, yoksa başka bir örnekle devam edelim mi?

Voltran Okul Analiz Sistemi