← Ana Rapor / ALAATTİN ARAS ULUSOY / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
07 December 2025, 16:34
Bitiş
Devam ediyor
Süre
15 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Detaylı Değerlendirme

Genel Değerlendirme
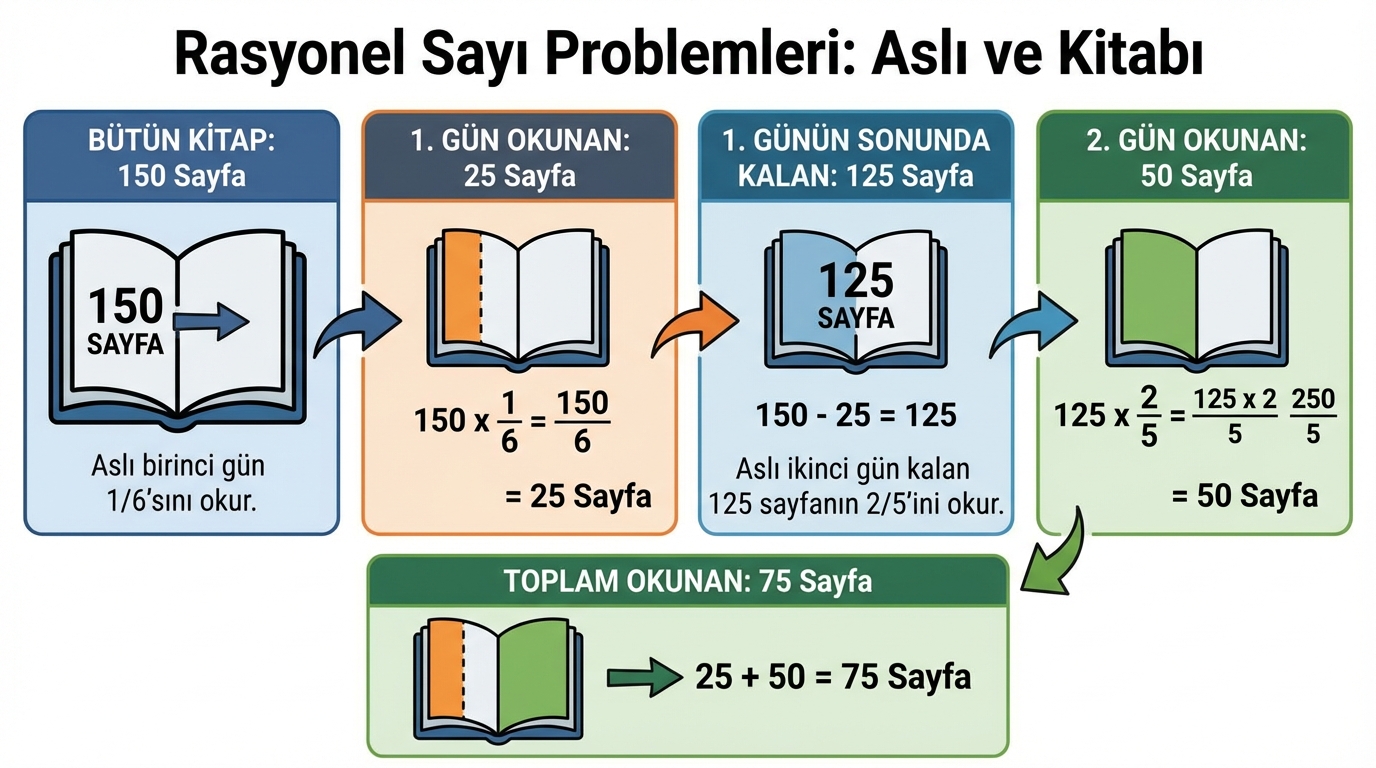
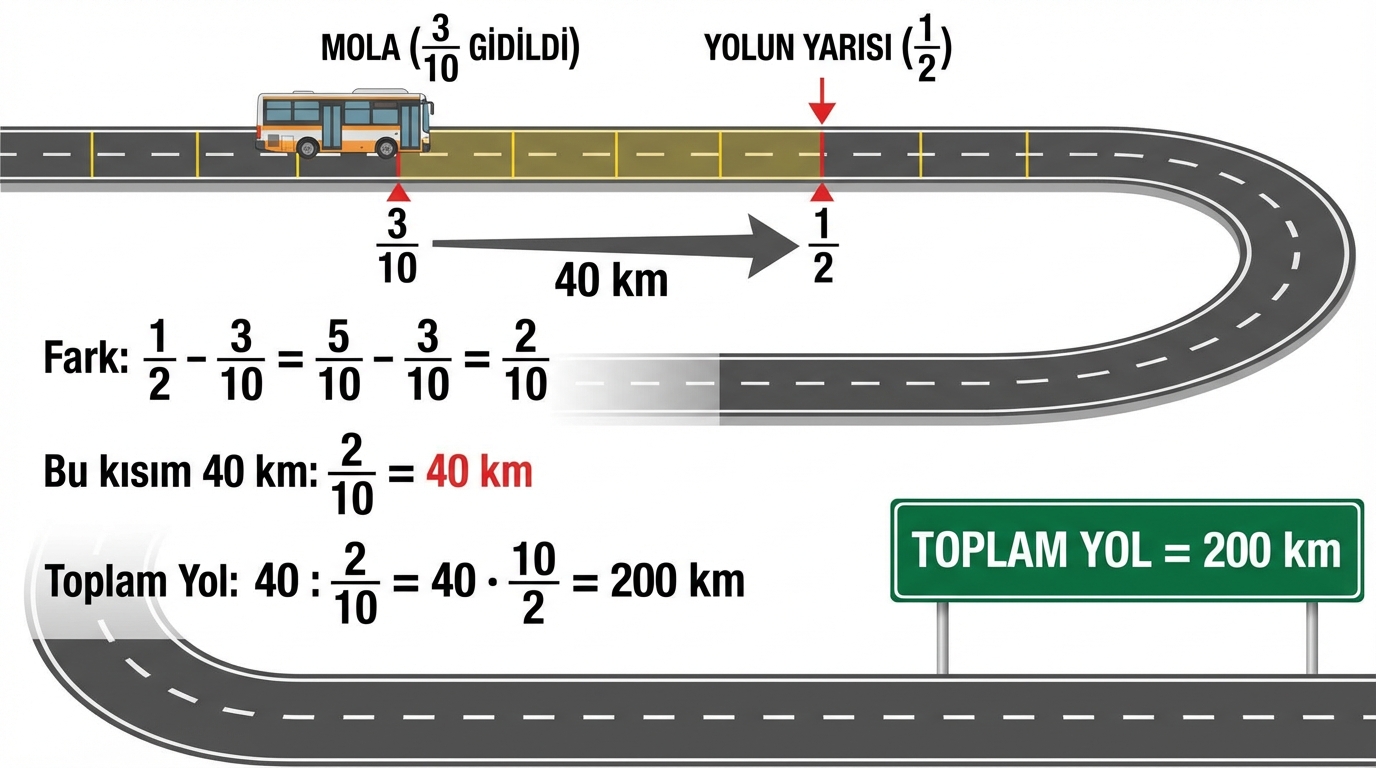
Öğrenci, "Rasyonel Sayı Problemleri" alt konusu üzerinde oldukça başarılı bir performans sergilemiştir. Dersin başında konunun detaylı anlatılmasını istemesine rağmen, sorulan tüm problem çözme ve hata tespiti sorularını doğru ve açıklayıcı bir şekilde yanıtlamıştır. Özellikle, çok adımlı problemlerde sıkça yapılan "kalanın kesrini" bulma gibi kritik hataları başarıyla tespit etmesi, konunun mantığını iyi kavradığını göstermektedir. Rasyonel sayılarla toplama ve çarpma işlemlerini problem senaryoları içinde doğru bir şekilde uygulamıştır. Öğrencinin konuyla ilgili belirgin bir eksiği gözlemlenmemiştir.

Öğrencinin İyi Olduğu Konular
- Rasyonel Sayılarla İşlemler: Öğrenci, ders boyunca rasyonel sayılarla toplama, çıkarma, çarpma ve bölme işlemlerini içeren problemleri çözme becerisini göstermiştir.
- Rasyonel Sayı Problemleri: Bu alt konuda öğrenci özellikle başarılıdır. Problemi anlama, çözüm için gerekli adımları belirleme ve işlemleri doğru bir şekilde uygulama konusunda yetkinlik göstermiştir. Çok adımlı problemleri ve hata analizi sorularını sorunsuz bir şekilde çözmüştür.

Öğrencinin Eksik Olduğu Konular
Bu ders seansı boyunca öğrencinin herhangi bir konu, alt konu veya kazanımda belirgin bir eksikliği tespit edilmemiştir.

Ders Dışı Yorumlar
- "anladım hocam ve burayı az önce çözmüştük" (Öğrenci, yapay zeka öğretmenin bir önceki örneği tekrar açıkladığını belirtmiştir.)

📜 Oturum Detayları

16:34:52
Öğrenci
Evet, hazırım Hocam! Bu konuyu detaylıca anlatır mısın?
16:34:52
💭 AI Öğretmen
Tabii, hemen başlıyorum
16:34:55
AI Öğretmen
Rasyonel sayılarla problemler, rasyonel sayıların yani kesirli sayıların toplama, çıkarma, çarpma ve bölme işlemlerinin günlük hayat durumlarına uyarlanarak ortaya çıkan soru tipleridir.
16:34:56
AI Öğretmen
Bu tip problemler, tam sayılarla yapılan problemlere çok benzer şekilde ele alınır. Çünkü temel mantık aynıdır.
16:34:58
AI Öğretmen
Bir problemi çözerken ilk olarak, elimizde hangi bilgiler bulunduğunu ve bizden neyin istenildiğini tespit ederiz. Yani verilenler ve istenenler belirlenir.
16:35:00
AI Öğretmen
Verilenler, soruda bize açıkça verilen bilgilerdir. İstenenler ise ulaşmamız gereken cevaptır.
16:35:02
AI Öğretmen
Verilen ve istenenleri belirledikten sonra, rasyonel sayılar arasındaki ilişkileri göz önünde bulundurarak bir çözüm planı oluşturulur.
16:35:04
AI Öğretmen
Bu çözüm planında, hangi rasyonel sayı işlemlerinin yapılacağına ve bu işlemlerin hangi sırayla uygulanacağına karar verilir.
16:35:07
AI Öğretmen
Son olarak, oluşturulan çözüm planına uygun şekilde işlemler adım adım yapılır ve ulaşılan sonucun, problemin bizden istediği cevaba uyup uymadığı kontrol edilir.
16:35:08
AI Öğretmen
Rasyonel sayılarla problemler konusunda anlattıklarımı anladın mı?
16:36:18
Öğrenci
Anladım
16:36:21
💭 AI Öğretmen
Şimdi bir soruya geçelim
16:36:21
❓ Soru medium
Bir geziye katılan 48 kişilik bir grubun 3/8'ü erkek öğrencidir. Gruptaki kız öğrencilerin ise 1/3'ü gözlüklüdür. Bu problemi çözen bir öğrencinin adımları aşağıda verilmiştir: 1. Adım: Erkek öğrenci sayısını bulmak için 48'i 3/8 ile çarparım: 48 * (3/8) = 18 erkek öğrenci. 2. Adım: Kız öğrenci sayısını bulmak için toplam kişi sayısından erkek öğrenci sayısını çıkarırım: 48 - 18 = 30 kız öğrenci. 3. Adım: Gözlüklü kız öğrenci sayısını bulmak için toplam öğrenci sayısını 1/3 ile çarparım: 48 * (1/3) = 16 gözlüklü kız öğrenci. 4. Adım: Grupta 16 tane gözlüklü kız öğrenci vardır. Bu öğrenci, çözümün bir adımında hata yapmıştır. Hatalı olan adım hangisidir ve bu gruptaki gözlüklü kız öğrenci sayısı gerçekte kaçtır?
16:37:17
Öğrenci
Cevabım: 3. adım 10 gözlüklü kız öğrenci olması lazım
16:37:18
💭 AI Öğretmen
Hemen Bakıyorum
16:37:23
AI Öğretmen
Harika bir iş çıkardın! Cevabın kesinlikle doğru!
16:37:24
AI Öğretmen
Üçüncü adımda yapılan hatayı ve doğru gözlüklü kız öğrenci sayısını tam isabetle belirlemişsin.
16:37:26
AI Öğretmen
Bu tür problemlerde, bir grubun belirli bir kısmını hesaplarken, o kısmın ait olduğu "bütün"ü doğru seçmek çok önemlidir.
16:37:28
AI Öğretmen
Yani, gözlüklü kız öğrencileri bulmak için tüm kız öğrencilerin sayısını temel alman gerektiğini çok iyi anlamışsın!
16:37:29
AI Öğretmen
Hatalı adım 3. adımdır ve grupta 10 gözlüklü kız öğrenci vardır.
16:37:29
AI Öğretmen
Derse devam edelim mi?
16:37:54
Öğrenci
Olur, devam edelim
16:37:55
💭 AI Öğretmen
Devam edelim o halde
16:38:10
Görsel
Görsel
16:38:13
AI Öğretmen
Rasyonel sayı problemleri, bir bütünün belirli bir kesir kadarının alınması, satılması veya kullanılması gibi durumları anlatır.
16:38:14
AI Öğretmen
Örneğimizde kirazların önce $\dfrac{2}{5}$’i öğleden önce satılıyor.
16:38:15
AI Öğretmen
Sonra, kalan kirazların değil, tüm kirazların $\dfrac{1}{3}$’ü öğleden sonra satılıyor.
16:38:16
AI Öğretmen
Günün sonunda satılan toplam kiraz oranını bulmamız isteniyor.
16:38:17
AI Öğretmen
Bu oranı bulmak için iki farklı kesiri topluyoruz, yani rasyonel sayılarda toplama işlemi yapmamız gerekiyor.
16:38:19
AI Öğretmen
Kesirleri toplarken önce paydalarını aynı yapmamız gerekir, yani payda eşitlemesi yaparız.
16:38:21
AI Öğretmen
Burada 5 ve 3'ün ortak paydası 15'tir.
16:38:24
AI Öğretmen
Öyleyse $\dfrac{2}{5}$ kesirini $\dfrac{6}{15}$, $\dfrac{1}{3}$ kesirini de $\dfrac{5}{15}$ olarak yazarız.
16:38:25
AI Öğretmen
Artık iki kesirin paydaları aynı olduğu için direkt toplayabiliriz: $\dfrac{6}{15} + \dfrac{5}{15}$.
16:38:27
AI Öğretmen
Bu toplama işleminin sonucu $\dfrac{11}{15}$'tir.
16:38:28
AI Öğretmen
Yani, gün sonunda kirazların $\dfrac{11}{15}$’i satılmış olur.
16:38:30
AI Öğretmen
Anlattıklarımı bu noktaya kadar anladın mı?
16:39:12
Öğrenci
Anladım
16:39:14
💭 AI Öğretmen
Şimdi bir soruya geçelim
16:39:14
❓ Soru medium
Bir çiftçi, tarlasının önce $\dfrac{2}{7}$'sini, sonra da $\dfrac{1}{4}$'ünü sürüyor. Çiftçinin bir öğrencisi olan Elif, tarlanın sürülmeden kalan kısmını hesaplarken aşağıdaki adımları izliyor: 1. Adım: Sürülen toplam alanı bulmak için $\dfrac{2}{7}$ ile $\dfrac{1}{4}$'ü toplarım. 2. Adım: Paydaları eşitlemek için birinci kesri 4 ile, ikinci kesri 7 ile genişletirim: $\dfrac{8}{28} + \dfrac{7}{28}$ 3. Adım: Payları kendi arasında, paydaları kendi arasında toplarım: $\dfrac{8+7}{28+28} = \dfrac{15}{56}$ 4. Adım: Kalan kısmı bulmak için bütünden, yani 1'den, bulduğum sonucu çıkarırım: $1 - \dfrac{15}{56} = \dfrac{41}{56}$ Elif'in çözümünde ilk hata hangi adımda yapılmıştır ve bu problemin doğru cevabı nedir?
16:40:00
Öğrenci
Cevabım: 3. adım, paydalar toplanamaz
16:40:01
💭 AI Öğretmen
Hemen Bakıyorum
16:40:07
AI Öğretmen
Harika bir iş çıkardın!
16:40:08
AI Öğretmen
Kesinlikle doğru, Elif 3. adımda paydaları da toplayarak bir hata yapmış.
16:40:10
AI Öğretmen
Kesirleri toplarken paydalar eşitlendikten sonra sadece paylar toplanır, ortak payda ise aynı kalır.
16:40:11
AI Öğretmen
Bu kuralı hatırlaman çok önemli!
16:40:12
AI Öğretmen
Dolayısıyla doğru cevap $\dfrac{13}{28}$'dir.
16:40:12
AI Öğretmen
Derse devam edelim mi?
16:40:27
Öğrenci
Olur, devam edelim
16:40:29
💭 AI Öğretmen
Hemen devam edelim
16:40:34
Görsel
Görsel
16:40:38
AI Öğretmen
Rasyonel sayı problemlerinde, verilen bütünün kesirleri üzerinden işlem yapılarak okunan, kalan ya da yapılan miktarlar bulunur.
16:40:40
AI Öğretmen
Verilen durumda kitabın tamamı 150 sayfadır ve Aslı birinci gün bu kitabın $\tfrac{1}{6}$'sını okur; birinci gün okunan sayfa sayısı, bütün sayfa sayısının kesir ile çarpılmasıyla bulunur:
16:40:41
AI Öğretmen
$$150 \tfrac{1}{6} = \tfrac{150}{6} = 25 \text{ sayfa}$$
16:40:43
AI Öğretmen
Birinci günün sonunda kalan sayfa sayısı, toplam sayfa sayısından okunan sayfa sayısının çıkarılmasıyla elde edilir:
16:40:45
AI Öğretmen
$$150 - 25 = 125$$
16:40:48
AI Öğretmen
İkinci gün Aslı, kalan 125 sayfanın $\tfrac{2}{5}$'ini okur ve bu miktar çarpma işlemiyle hesaplanır:
16:40:51
AI Öğretmen
$$125 \tfrac{2}{5} = \tfrac{125 \times 2}{5} = \tfrac{250}{5} = 50 \text{ sayfa}$$
16:40:52
AI Öğretmen
Toplam okunan sayfa sayısı, birinci ve ikinci gün okunan sayfaların toplanmasıyla bulunur:
16:40:54
AI Öğretmen
$$25 + 50 = 75 \text{ sayfa}$$
16:40:55
AI Öğretmen
Bu kısmı anladın mı?
16:41:34
Öğrenci
Anladım
16:41:37
💭 AI Öğretmen
Şimdi bir soruya geçelim
16:41:37
❓ Soru medium
240 dönümlük bir tarlanın sahibi, tarlasının $\frac{1}{4}$'üne buğday, kalan tarlanın ise $\frac{2}{3}$'üne mısır ekiyor. Bir öğrenci, bu tarlada ekilmeyen alanı hesaplarken aşağıdaki adımları izliyor: 1. Adım: Buğday ekilen alan: $240 \times \frac{1}{4} = 60$ dönüm 2. Adım: Mısır ekilen alan: $240 \times \frac{2}{3} = 160$ dönüm 3. Adım: Toplam ekili alan: $60 + 160 = 220$ dönüm 4. Adım: Kalan alan: $240 - 220 = 20$ dönüm Bu öğrencinin çözümündeki hata hangi adımda yapılmıştır ve tarlanın ekilmeyen alanı gerçekte kaç dönümdür?
16:42:52
Öğrenci
Cevabım: 2. adım 240'tan 60'ı çıkarmamız gerek
16:42:53
💭 AI Öğretmen
Hemen Bakıyorum
16:42:58
AI Öğretmen
Harika bir iş çıkardın! Cevabın kesinlikle doğru!
16:42:59
AI Öğretmen
Öğrencinin hatası gerçekten de 2. adımdaydı, çünkü mısır ekilen alan tarlanın tamamının değil, buğday ekildikten sonra *kalan* kısmın üzerinden hesaplanmalıydı.
16:43:01
AI Öğretmen
Bu tür sorularda "kalanın" ifadesine dikkat etmek, doğru sonuca ulaşmak için çok önemli bir detaydır.
16:43:02
AI Öğretmen
Tarlanın ekilmeyen alanı 60 dönümdür.
16:43:03
AI Öğretmen
Derse devam edelim mi?
16:43:24
Öğrenci
Olur, devam edelim
16:43:24
💭 AI Öğretmen
Hemen ilerliyoruz
16:43:32
Görsel
Görsel
16:43:35
AI Öğretmen
Bir rasyonel sayı probleminde, yolun belirli bir kesri ile yolun yarısı gibi başka bir kesri karşılaştırarak bilinmeyen toplam uzunluk bulunabilir.
16:43:39
AI Öğretmen
Bu örnekte, bir otobüsün gideceği yolun $\frac{3}{10}$'unu tamamladıktan sonra mola verdiği belirtiliyor ve eğer otobüs 40 km daha gitseydi yolun $\frac{1}{2}$'sine ulaşacağı ifade ediliyor.
16:43:41
AI Öğretmen
Bu durumda yolun yarısını ifade eden $\frac{1}{2}$ kesri ile, şu ana kadar gidilen yolu ifade eden $\frac{3}{10}$ kesri arasındaki mesafe 40 km'ye karşılık geliyor.
16:43:43
AI Öğretmen
Aradaki mesafeyi bulmak için, kesirler birbirinden çıkarılır:
16:43:46
AI Öğretmen
$\frac{1}{2} - \frac{3}{10} = \frac{5}{10} - \frac{3}{10} = \frac{2}{10}$
16:43:48
AI Öğretmen
Yani, yolun $\frac{2}{10}$'luk kısmı 40 km'ye eşittir.
16:43:51
AI Öğretmen
Yolun tamamını bulmak için, 40 km'lik mesafeyi $\frac{2}{10}$ kesirine böleriz:
16:43:53
AI Öğretmen
$40 : \frac{2}{10} = 40 \cdot \frac{10}{2} = \frac{40 \cdot 10}{2} = \frac{400}{2} = 200$
16:43:54
AI Öğretmen
Bu hesaplamanın sonucunda, yolun tamamının 200 km olduğu bulunur.
16:43:55
AI Öğretmen
Anlattığım kısmı anladın mı?
16:44:43
Öğrenci
Anladım
16:44:45
💭 AI Öğretmen
Şimdi bir soruya geçiyoruz
16:44:46
❓ Soru medium
Bir su deposunun önce $\frac{1}{4}$'ü, daha sonra da $\frac{1}{6}$'sı su ile dolduruluyor. Eğer depoya 50 litre daha su eklenseydi deponun $\frac{3}{4}$'ü dolmuş olacaktı. Buna göre, bu su deposunun tamamı kaç litre su alır?
16:46:35
Öğrenci
Cevabım: 150 L
16:46:36
💭 AI Öğretmen
Güzel, devam ediyoruz
16:46:36
Görsel
Görsel
16:46:40
AI Öğretmen
Rasyonel sayı problemlerinde, bir bütünü parçalara ayırırken kesirlerin bölüntü ve orantı ilişkileri esas alınır; miktarların belirlenmesinde ise verilen bütün üzerinde yapılan işlemler matematiksel modellemeyle çözülür.
16:46:43
AI Öğretmen
Buradaki örnekte, kitabın tamamı 150 sayfa olarak belirlenmiş ve Aslı, ilk gün bu kitabın $\frac{1}{6}$’sını okuyor.
16:46:46
AI Öğretmen
Bir büyüklüğün belirli bir kesir kadarı sorulduğunda çarpma işlemi kullandığımızın sebebi; bütünü, istenen miktar kadar eşit parçaya ayırıp, o parçalardan belirli bir kısmını almaktır.
16:46:48
AI Öğretmen
Bu durum, pratikte örneğin bir bütçenin belli bir oranının harcanmasında veya bir günün belirli bir bölümünün çalışmaya ayrılmasında da tamamen aynı şekilde geçerlidir.
16:46:50
AI Öğretmen
Örneğin: $150 \cdot \frac{1}{6} = \frac{150}{6} = 25$ sayfa okundu.
16:46:51
AI Öğretmen
Birinci günün sonunda kalan sayfa sayısını bulurken çıkarma işlemi yaparız; bu adımda, tam bütünden kısmi bütünü çıkararak aradaki farkı yani kalan işi belirleriz.
16:46:54
AI Öğretmen
Bu pratik olarak kalan iş miktarının tespiti ve takip edilmesinde kullanılır: $150 - 25 = 125$ sayfa kalır.
16:46:56
AI Öğretmen
İkinci gün, Aslı kalan 125 sayfanın $\frac{2}{5}$’ini okuyor; burada kesrin payı işlemin kaç katı yapılacağını, paydası ise bütünün kaç eşit parçaya bölüneceğini gösterir.
16:46:59
AI Öğretmen
Aynı yöntem, örneğin bir işin belirli oranlarda paylaşılması veya stokların kısmî olarak kullanılmasında uygulanır: $125 \cdot \frac{2}{5} = \frac{125 \times 2}{5} = \frac{250}{5} = 50$ sayfa okunur.
16:47:01
AI Öğretmen
İki gün boyunca okunan toplam sayfa miktarı, ardışık işlemlerin birikimli etkisini gösterir ve çok adımlı süreçlerde genel ilerlemenin takibini sağlar: $25 + 50 = 75$ sayfa okunmuştur.
16:47:01
AI Öğretmen
Anlattıklarımı anladın mı, yoksa açıklamamı istediğin bir bölüm var mı?
16:49:05
Öğrenci
anladım hocam ve burayı az önce çözmüştük
16:49:06
💭 AI Öğretmen
Devam edelim o halde
16:49:06
Görsel
Görsel
16:49:08
AI Öğretmen
Rasyonel sayılarla çözüm yapılan problemler genellikle oranlar arasındaki değişimi gözlemleyerek bilinmeyen değerlerin bulunmasına dayanır.
16:49:09
AI Öğretmen
Bu tür durumlarda, farklı kesirler bir bütünün farklı parçalarını gösterir ve bunlar arasındaki fark gerçek, ölçülebilir bir büyüklüğe dönüştürülür.
16:49:12
AI Öğretmen
Örneğin, bir otobüs yolun $\frac{3}{10}$'unu kat ettikten sonra mola verdiğinde ve ardından sadece 40 km daha giderek yolun $\frac{1}{2}$'sine ulaşabiliyorsa, burada yolun $\frac{3}{10}$'u ile $\frac{1}{2}$'si arasındaki bölüm 40 km anlamına gelir.
16:49:13
AI Öğretmen
Yani iki kesir arasındaki fark kadar yol almak 40 km'ye tekabül eder ve bu da oranların nasıl mutlak değerlere çevrildiğine dair bir örnektir.
16:49:15
AI Öğretmen
Bu gibi soruları çözerken, iki kesirin farkı, gerçek hayatta ne kadar mesafeye karşılık geldiği açısından analiz edilir ve matematiksel süreçte genellikle paydaları eşitleme ve ters kesirle çarpma kullanılır.
16:49:17
AI Öğretmen
Yukarıdaki örneği çözmek için, yolun yarısıyla o ana kadar gidilen yol arasındaki mesafe, kesirler ortak paydaya getirilerek hesaplanır: $$\frac{1}{2} - \frac{3}{10} = \frac{5}{10} - \frac{3}{10} = \frac{2}{10}$$
16:49:20
AI Öğretmen
Buradaki $\frac{2}{10}$'luk oran, 40 km'lik mesafeye karşılık gelmektedir.
16:49:22
AI Öğretmen
Tüm yolun uzunluğunu bulmak için bu kez 40 km'nin bütünün $\frac{2}{10}$'u olduğu kabul edilir ve ters orantı kurularak yolun tamamı bulunur: $40 \div \frac{2}{10} = 40 \times \frac{10}{2} = 200$ km.
16:49:24
AI Öğretmen
Bu yöntem, oran-proporsiyon prensiplerinin yol hesaplamaları, harita ölçeklendirmeleri ya da taksitlendirme işlemlerinde nasıl pratik olarak kullanılabileceğine de güzel bir örnek oluşturur.
16:49:25
AI Öğretmen
Anlattıklarımı bu kısmına kadar anladın mı?

Voltran Okul Analiz Sistemi