← Ana Rapor / DEFNE GÜDEN / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
22 October 2025, 07:39
Bitiş
Devam ediyor
Süre
8 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
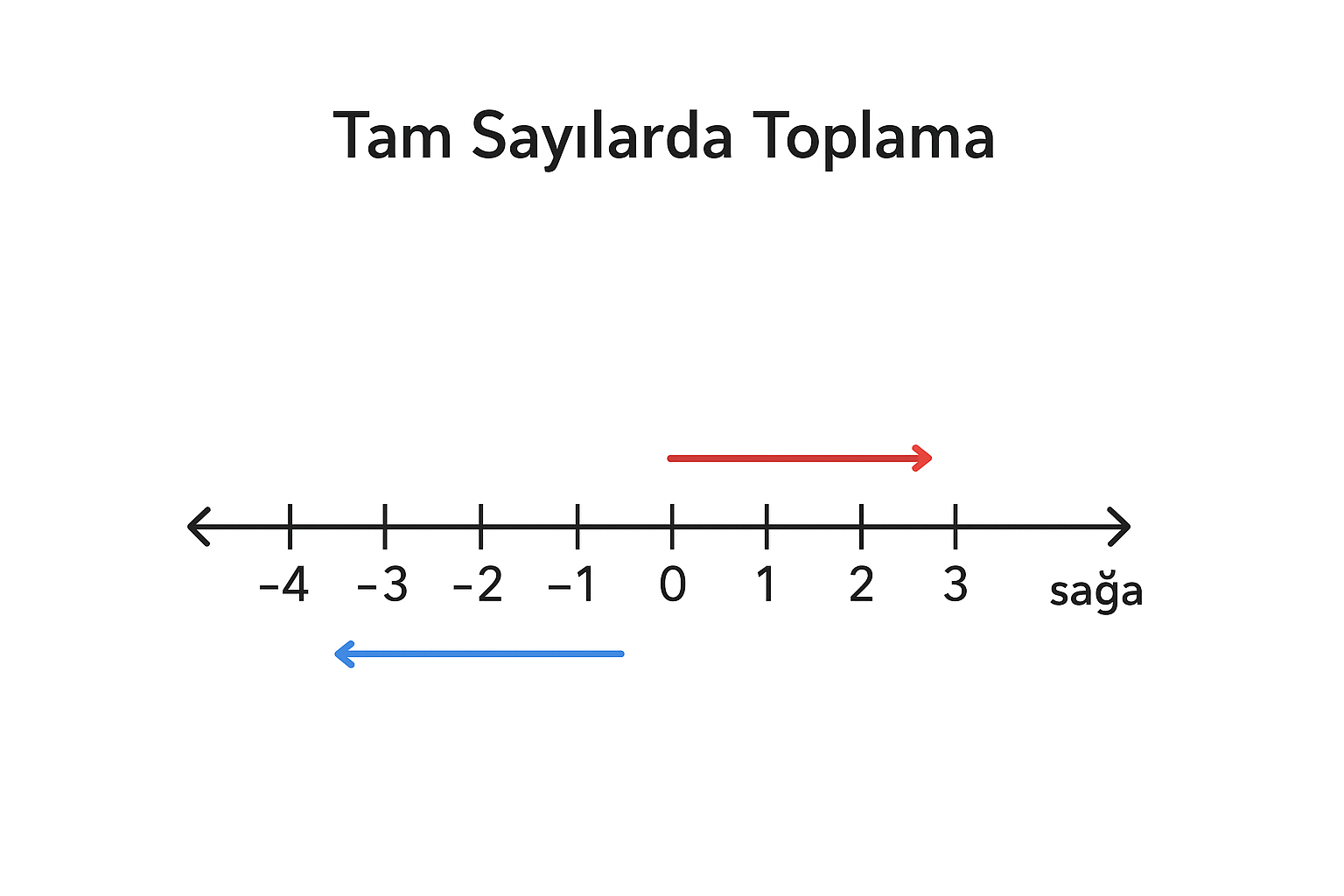
  • Tam Sayılarla İşlemler
Alt Konular:
  • Tam Sayılarla Toplama Ve Çıkarma
Kazanımlar:
  • Tam sayılarla toplama ve çıkarma işlemlerini yapar, ilgili problemleri çözer.
  • Toplama işleminin özelliklerini akıcı işlem yapmak için birer strateji olarak kullanır.

Detaylı Değerlendirme

Öğrenci Performans Analizi

Bu derste öğrencinin Tam Sayılarla İşlemler konusuna genel olarak hakim olduğu ancak bazı temel kavram ve özelliklerde kafa karışıklığı yaşadığı gözlemlenmiştir.

# Genel Değerlendirme
Öğrenci, pratik işlem yapma konusunda başarılı bir performans sergilemiştir. Zıt işaretli tam sayıların toplandığı bir problemi doğru bir şekilde çözmüş ve hatanın kaynağını net bir şekilde açıklamıştır. Bu, temel toplama becerilerinin yerinde olduğunu göstermektedir.

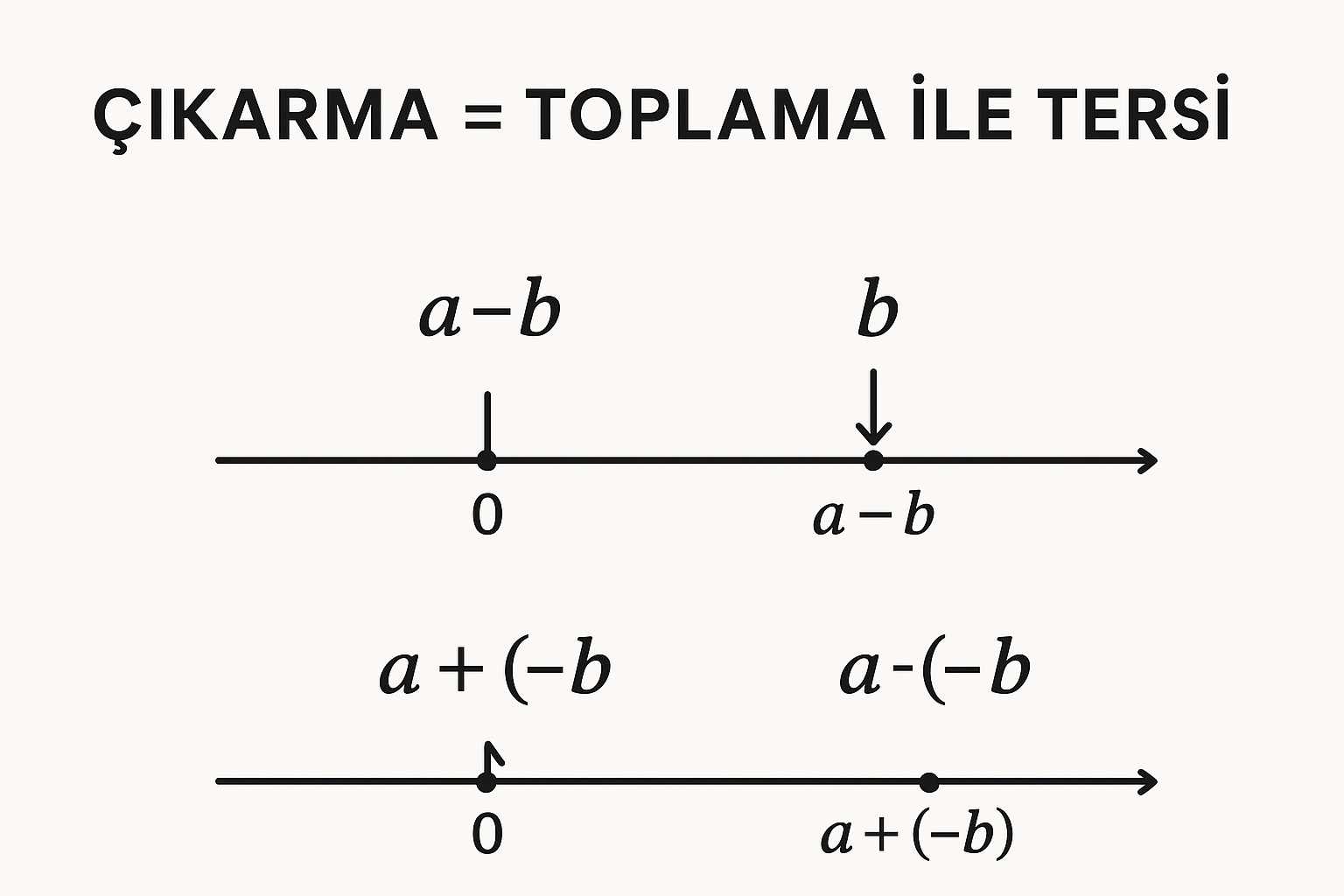
Ancak, konu teorik özelliklere geldiğinde öğrencinin zorlandığı görülmektedir. Özellikle toplama işleminin değişme ve birleşme özelliklerini karıştırdığını kendisi ifade etmiş ve tekrar anlatılmasını istemiştir. Bu teorik bilgilerin önemini ve mantığını kavramak için ek sorular sorması, konuyu ezberlemek yerine anlamaya çalıştığını gösteren olumlu bir işarettir, fakat aynı zamanda bu alanlarda eksiklikleri olduğunu da teyit etmektedir. Çıkarma işleminin toplamanın tersi olduğu kavramıyla ilgili sorduğu "nasıl kanıtlayabiliriz?" sorusu da bu durumu desteklemektedir.

# Öne Çıkanlar
- İyi Olduğu Alanlar: Öğrenci, zıt işaretli tam sayıları toplama ve problemdeki hatayı mantıksal olarak tespit etme konusunda başarılıdır. Etkisiz eleman (0) kavramını anladığını ve soruda doğru bir şekilde kullandığını göstermiştir.
- Geliştirilmesi Gereken Alanlar: Toplama işleminin özellikleri (değişme, birleşme) konusunda belirgin bir kafa karışıklığı yaşamaktadır. İşlemlerin arkasındaki teorik ve kavramsal bilgileri güçlendirmesi gerekmektedir.

Sonuç olarak, öğrencinin işlem yapma yeteneği iyi seviyededir ancak konunun teorik altyapısını ve özelliklerini daha iyi anlaması için bu alanlara odaklanılması faydalı olacaktır.

📜 Oturum Detayları

07:39:34
Öğrenci
Evet, hazırım Hocam! Bu konuyu detaylıca anlatır mısın?
07:39:34
💭 AI Öğretmen
Hemen başlıyoruz
07:39:34
Görsel
Görsel
07:39:34
AI Öğretmen
Tam sayılarla toplama işleminde, iki sayının işaretleri aynı ise önce sayıların mutlak değerleri toplanır, ardından ortak işaret sonuca eklenir.
07:39:34
AI Öğretmen
Örneğin, iki negatif tam sayı toplandığında, \(-3 + (-5) = -(3 + 5) = -8\) şeklinde hesaplanır.
07:39:34
AI Öğretmen
Sayı doğrusunda toplama yaparken, eklenen sayı pozitifse sağa doğru, negatifse sola doğru hareket edilir.
07:39:34
AI Öğretmen
\(+\) işaretli bir sayı ekleniyorsa, örneğin \(3 + 2\) işleminde sağa 2 birim ilerlenir.
07:39:35
AI Öğretmen
\(-\) işaretli bir sayı ekleniyorsa, örneğin \(-4 + (-3)\) işleminde sola 3 birim ilerlenir.
07:39:35
AI Öğretmen
Zıt işaretli iki tam sayı toplandığında, sayıların mutlak değerleri arasındaki fark alınır.
07:39:35
AI Öğretmen
Bu farkın sonucuna, mutlak değeri daha büyük olan sayının işareti verilir.
07:39:35
AI Öğretmen
Örneğin, \(7 + (-10) = -(10 - 7) = -3\) şeklinde bulunur.
07:39:35
AI Öğretmen
Bu açıklamayı anladın mı?
07:40:15
Öğrenci
Anladım
07:40:15
💭 AI Öğretmen
Harika, şimdi bir soruya geçelim
07:40:15
❓ Soru medium
Ali, `(-15) + 9 + (-5)` işleminin sonucunu bulmaya çalışırken ilk olarak `(-15) + 9` işlemini yapmış ve sonucu 6 bulmuştur. Ardından, bulduğu bu sonuç ile `(-5)` sayısını toplayarak nihai cevabı 1 olarak hesaplamıştır. Ali'nin çözümündeki hata nedir ve bu işlemin doğru sonucu kaçtır?
07:42:12
Öğrenci
Cevabım: yanlış bulmasının sebebi -15 +9'u - 6 yerine +6 bulmuştur doğru Cevap -11dir
07:42:12
💭 AI Öğretmen
Kontrol ediyorum
07:42:12
AI Öğretmen
Harika bir iş çıkardın! Ali'nin hatasını ve işlemin doğru sonucunu mükemmel bir şekilde bulmuşsun.
07:42:12
AI Öğretmen
Zıt işaretli tam sayıları toplarken, mutlak değeri büyük olan sayının işaretini almamız gerektiğini çok iyi anlamışsın. Bu, tam sayılarla işlemlerde çok önemli bir kural!
07:42:12
AI Öğretmen
Bu sayede `(-15) + 9` işleminin `+6` değil, `-6` olduğunu doğru tespit ettin ve sonuca ulaştın.
07:42:12
AI Öğretmen
Doğru cevap -11'dir.
07:42:12
AI Öğretmen
Derse devam edelim mi?
07:42:56
Öğrenci
Olur, devam edelim
07:42:57
💭 AI Öğretmen
Hemen ilerliyoruz
07:42:57
Görsel
Görsel
07:42:57
AI Öğretmen
Tam sayılarla toplama işleminin dört temel özelliği vardır: değişme, birleşme, etkisiz eleman ve ters eleman.
07:42:57
AI Öğretmen
Değişme özelliği, toplama işleminde sayıların yerini değiştirsen de sonucun aynı kalacağını söyler.
07:42:57
AI Öğretmen
Örneğin 7 + (-5) = (-5) + 7 olur.
07:42:57
AI Öğretmen
Birleşme özelliği, üç ya da daha fazla tam sayı toplandığında, hangi iki sayı önce toplanırsa sonucun aynı olacağını ifade eder.
07:42:57
AI Öğretmen
Örneğin [2 + (-5)] + 4 = 2 + [(-5) + 4] = 1; her iki grupta da sonuç aynıdır.
07:42:57
AI Öğretmen
Etkisiz eleman özelliği, 0 sayısının toplama işleminde etkisiz olduğunu gösterir.
07:42:57
AI Öğretmen
Yani -12 + 0 = 0 + (-12) = -12 ve 0 + 9 = 9 + 0 = 9.
07:42:57
AI Öğretmen
Ters eleman özelliği, bir tam sayı ile toplandığında sonucu 0 yapan sayıyı tanımlar.
07:42:58
AI Öğretmen
Örneğin (+3) + (-3) = 0; bu iki sayı birbirinin toplama işlemine göre tersi sayılardır.
07:42:58
AI Öğretmen
Tam sayılarla toplama işleminin bu dört temel özelliğini anladın mı?
07:44:22
Öğrenci
Ben kendimi bu konuda eksik hissediyorum özellikle birleşme ve değişme özelliklerini karıştırıyorum tekrar yavaş bir şekilde anlatabilir misin
07:44:22
💭 AI Öğretmen
Elbette, hemen toparlıyorum
07:44:23
AI Öğretmen
Tabii, değişme ve birleşme özelliklerini yavaşça açıklayalım.
07:44:23
AI Öğretmen
Değişme özelliği, toplama işleminde sayıların yerini değiştirdiğimizde sonucun değişmemesi demektir. Mesela, \(7 + (-5) = (-5) + 7\) olur; sonuç her iki durumda da aynıdır.
07:44:23
AI Öğretmen
Birleşme özelliği ise üç veya daha fazla sayı toplarken hangi ikisini önce toplarsak toplayalım sonucun değişmemesidir. Örneğin, \([2 + (-5)] + 4 = 2 + [(-5) + 4]\) işlemlerinin sonucu aynıdır.
07:44:23
AI Öğretmen
Yani değişme özelliği sayıları yer değiştirirken, birleşme özelliği toplama işleminin sırasını değiştirmemizle ilgilidir.
07:44:23
AI Öğretmen
Bunu anladın mı, biraz daha örnekle açıklamamı ister misin?
07:45:08
Öğrenci
Değişme özelliği toplama işleminde neden önemlidir?
07:45:09
💭 AI Öğretmen
Hemen açıklıyorum
07:45:09
AI Öğretmen
Değişme özelliği toplama işleminde çok önemlidir çünkü sayıların yerini değiştirdiğimizde sonucu değiştirmemesi, işlemi daha esnek ve kolay yapmamızı sağlar.
07:45:09
AI Öğretmen
Bu sayede toplama işleminde sayıları istediğimiz sırayla toplayabiliriz, bu da hesaplamayı hızlandırır ve hata yapma riskini azaltır.
07:45:09
AI Öğretmen
Örneğin, \(7 + (-5)\) işlemi ile \((-5) + 7\) işlemi aynı sonucu verir, böylece hangi sayıyı önce yazarsak yazalım sonuç değişmez.
07:45:09
AI Öğretmen
Bunu anladın mı?
07:45:39
Öğrenci
Anladım
07:45:39
💭 AI Öğretmen
Hemen bir soru geliyor
07:45:39
❓ Soru medium
`(-25) + (+13) + A + (+25) + (-9) = (+13) + (-9)` eşitliğinin doğru olması için A yerine hangi tam sayı gelmelidir?
07:46:20
Öğrenci
Cevabım: 0
07:46:20
💭 AI Öğretmen
Kontrol ediyorum
07:46:20
AI Öğretmen
Harika bir iş çıkardın! Cevabın kesinlikle doğru!
07:46:20
AI Öğretmen
Eşitliğin her iki tarafında da aynı ifadeler olduğundan, A'nın 0 olması dengeyi korur.
07:46:20
AI Öğretmen
Bu, toplama işleminde etkisiz eleman özelliğini ve zıt işaretli sayıların birbirini sıfırladığını çok iyi anladığını gösteriyor. Süper!
07:46:20
AI Öğretmen
Dolayısıyla doğru cevap 0'dır.
07:46:20
AI Öğretmen
Derse devam edelim mi?
07:47:00
Öğrenci
Olur, devam edelim
07:47:00
💭 AI Öğretmen
Tamam, devam ediyoruz
07:47:00
Görsel
Görsel
07:47:01
AI Öğretmen
Çıkarma yaparken, çıkan sayının toplama işlemine göre tersi alınır.
07:47:01
AI Öğretmen
Bu ters sayı, eksilen sayı ile toplanır.
07:47:01
AI Öğretmen
Matematiksel olarak bu, \(a - b = a + (-b)\) şeklinde gösterilir.
07:47:01
AI Öğretmen
Burada \(a\), eksilen sayıyı; \(b\) ise çıkan sayıyı ifade eder.
07:47:01
AI Öğretmen
Çıkarma, toplamanın ters işlemi olarak düşünülebilir.
07:47:01
AI Öğretmen
Sonuç, eksilen sayıya çıkan sayının toplama işlemine göre tersinin eklenmesiyle bulunur.
07:47:01
AI Öğretmen
Tam sayılarla çıkarma işleminin toplama işlemiyle ilişkisini anladın mı?
07:47:35
Öğrenci
Çıkarma işleminin toplama işleminin tersi olduğunu nasıl kanıtlayabiliriz?
07:47:35
💭 AI Öğretmen
Düşünüyorum, biraz sabret
07:47:35
AI Öğretmen
Çıkarma işleminin toplama işleminin tersi olduğunu kanıtlamak için, çıkarma işlemini toplama işlemi cinsinden yazabiliriz.
07:47:36
AI Öğretmen
Örneğin, \(a - b\) işlemini \(a + (-b)\) olarak ifade ederiz; burada \(-b\), \(b\) sayısının toplama işlemine göre tersidir.
07:47:36
AI Öğretmen
Bu şekilde çıkarma, toplama işleminin tersini almak demektir.
07:47:36
AI Öğretmen
Ayrıca, toplama işlemiyle bir sayıya tersini eklediğimizde sonuç sıfır olur; bu da ters işlemin varlığını gösterir.
07:47:36
AI Öğretmen
Yani, çıkarma işlemi aslında toplama işlemine ters sayı eklemekle aynıdır ve bu yüzden toplamanın tersidir.
07:47:36
AI Öğretmen
Bunu anladın mı?

Voltran Okul Analiz Sistemi