Oturum Detayları - a262ab92-a1e8-4724-b43a-61c0a1a36877

14:29:03

Öğrenci

Evet, hazırım Hocam! Bu konuyu detaylıca anlatır mısın?

14:29:04

💭 AI Öğretmen

Hemen başlıyoruz

14:29:04

Görsel

14:29:06

AI Öğretmen

Her doğal sayı, iki tane doğal sayının çarpımı olarak yazılabilir.

14:29:08

AI Öğretmen

Bu şekilde çarpılan iki sayıya, ilgili doğal sayının çarpanları denir.

14:29:10

AI Öğretmen

Bir doğal sayının pozitif tam sayı çarpanları, o sayıyı kalansız bölebilen pozitif tam sayılardır.

14:29:10

AI Öğretmen

Yani, pozitif tam sayı çarpanları aynı zamanda o sayının bölenleridir.

14:29:11

AI Öğretmen

Çarpanlar konusu bize bir sayının hangi sayılara bölünebildiğini gösterir.

14:29:12

AI Öğretmen

Örneğin; 6 sayısının çarpanları 1, 2, 3 ve 6'dır.

14:29:14

AI Öğretmen

Bu sayılar, 6'yı kalansız bölebilen pozitif tam sayılardır.

14:29:15

AI Öğretmen

Pozitif tam sayıların çarpanlarını bulmak, çarpanlar ve katlar konusunun temelidir.

14:29:16

AI Öğretmen

Bu kısmı anladın mı, yoksa çarpanlar konusunda açıklamamı istediğin bir bölüm var mı?

14:29:44

Öğrenci

Anladım

14:29:47

💭 AI Öğretmen

Şimdi soruya geçiyorum

14:29:47

❓ Soru medium

$A$ pozitif tam sayısının pozitif tam sayı çarpanlarının sayısı $15$'tir. $A \lt 500$ olduğuna göre, $A$'nın alabileceği tüm değerlerin toplamı kaçtır?

14:30:01

Öğrenci

Cevabım: bilmem

14:30:02

💭 AI Öğretmen

Hemen Bakıyorum

14:30:06

AI Öğretmen

Cevabınız doğru değil, çünkü soruyu çözmek için matematiksel bir işlem yapmanız gerekiyor.

14:30:10

AI Öğretmen

Bir sayının pozitif tam sayı çarpanlarının sayısını bulmak için sayıyı asal çarpanlarına ayırırız ve üslerine 1 ekleyip çarparız. Örneğin, $A = x^a \cdot y^b \cdot z^c \dots$ ise çarpan sayısı $(a+1)(b+1)(c+1)\dots$ olur.

14:30:13

AI Öğretmen

Soruda çarpan sayısı 15 olarak verilmiş, yani $(a+1)(b+1)(c+1)\dots = 15$ olmalı. 15 sayısını çarpanlarına ayırdığımızda ya tek bir sayı olarak (15) ya da $3 \times 5$ şeklinde iki sayı olarak yazabiliriz.

14:30:15

AI Öğretmen

Eğer tek asal sayının kuvveti ise, $(a+1) = 15$ yani $a = 14$ olur. Bu durumda sayı $x^{14}$ olur. En küçük asal sayı 2 olduğu için $2^{14} = 16384$ olur ki bu 500’den büyüktür, bu yüzden bu durum geçerli değil.

14:30:18

AI Öğretmen

Diğer durumda ise sayı iki asal sayının kuvvetlerinin çarpımıdır: $(a+1)(b+1) = 3 \times 5$ veya $5 \times 3$. Yani $a=2$, $b=4$ veya $a=4$, $b=2$ olabilir.

14:30:22

AI Öğretmen

Şimdi en küçük asal sayıları kullanarak sayıları bulalım: - $2^4 \times 3^2 = 16 \times 9 = 144$ - $3^4 \times 2^2 = 81 \times 4 = 324$ - $2^4 \times 5^2 = 16 \times 25 = 400$ Bunların hepsi 500’den küçüktür.

14:30:24

AI Öğretmen

Başka kombinasyonlar 500’den büyük olacağı için sadece bu üç sayı geçerlidir. Bu sayıların toplamı $144 + 324 + 400 = 868$ olur.

14:30:26

AI Öğretmen

Yani, $A$ sayısının alabileceği tüm değerlerin toplamı 868’dir. Öğrenmeye devam etmeniz çok güzel, böyle soruları adım adım çözmeye çalışırsanız çok daha iyi anlayabilirsiniz!

14:30:26

AI Öğretmen

Derse devam edelim mi?

14:31:58

Öğrenci

Olur, devam edelim

14:31:59

💭 AI Öğretmen

Devam ediyoruz hemen

14:32:08

Görsel

14:32:10

AI Öğretmen

Bir sayının çarpanları, o sayıyı kalansız bölen pozitif tam sayılardır.

14:32:11

AI Öğretmen

24 sayısının çarpanlarını bulmak için çarpan çiftlerini inceleyebiliriz: 1 × 24, 2 × 12, 3 × 8, 4 × 6.

14:32:13

AI Öğretmen

Buradan hareketle, 24'ü kalansız bölen pozitif tam sayılar şunlardır: 1, 2, 3, 4, 6, 8, 12 ve 24.

14:32:15

AI Öğretmen

Bu sayıların her biri, 24'ü başka bir pozitif tam sayı ile çarptığımızda sonucu 24 yapan sayılardır.

14:32:16

AI Öğretmen

Yani, örneğin 2 × 12 = 24 olduğu için hem 2 hem de 12, 24'ün çarpanlarıdır.

14:32:18

AI Öğretmen

Aynı şekilde 3 × 8 = 24 ve 4 × 6 = 24 çarpımlarını da kontrol ederek diğer çarpanları bulabiliriz.

14:32:20

AI Öğretmen

Böylece 24'ü kalansız bölen pozitif tam sayılar 1, 2, 3, 4, 6, 8, 12 ve 24 olur.

14:32:22

AI Öğretmen

Anlattıklarımı anladın mı?

14:33:01

Öğrenci

Anladım

14:33:03

💭 AI Öğretmen

Şimdi bir soru soracağım

14:33:04

❓ Soru medium

Alanı $72$ cm$^2$ olan bir dikdörtgenin kenar uzunlukları, santimetre cinsinden $1$'den büyük birer tam sayıdır. Bu dikdörtgenin çevre uzunluğunun alabileceği kaç farklı tam sayı değeri vardır?

14:33:37

Öğrenci

Bir ipucu verir misiniz hocam?

14:33:38

💭 AI Öğretmen

Tabii, bakalım

14:33:41

AI Öğretmen

Alanı 72 olan bir dikdörtgenin kenar uzunlukları hangi sayılar olabilir, bu sayılar nasıl bulunur?

14:33:43

AI Öğretmen

Alan 72 olduğuna göre, kenar uzunluklarının çarpımı 72'ye eşit olmalı, peki 72'nin tam sayı çarpanlarını nasıl bulabiliriz?

14:33:45

AI Öğretmen

Kenar uzunluklarının 1'den büyük tam sayılar olduğunu düşünürsek, 72'nin hangi çarpan çiftleri bu koşulu sağlar?

14:35:17

Öğrenci

Cevabım: 5

14:35:18

💭 AI Öğretmen

Hemen Bakıyorum

14:35:23

AI Öğretmen

Harika bir iş çıkardın! Cevabın kesinlikle doğru.

14:35:25

AI Öğretmen

Alanı 72 cm$^2$ olan bir dikdörtgenin kenar uzunlukları için 1'den büyük tüm çarpan çiftlerini buldun ve her bir çift için çevre uzunluğunu doğru bir şekilde hesapladın.

14:35:27

AI Öğretmen

Bu tür sorularda, tüm olası durumları gözden geçirmek (çarpan çiftlerini bulmak gibi) ve her bir durum için istenen değeri (çevre uzunluğu gibi) hesaplamak çok önemlidir.

14:35:28

AI Öğretmen

Farklı çevre uzunluklarının sayısını bularak ne kadar dikkatli olduğunu gösterdin. Tebrikler!

14:35:29

AI Öğretmen

Doğru cevap 5'tir.

14:35:29

AI Öğretmen

Derse devam edelim mi?

14:35:57

Öğrenci

Olur, devam edelim

14:35:58

💭 AI Öğretmen

Harika, ilerliyoruz

14:36:05

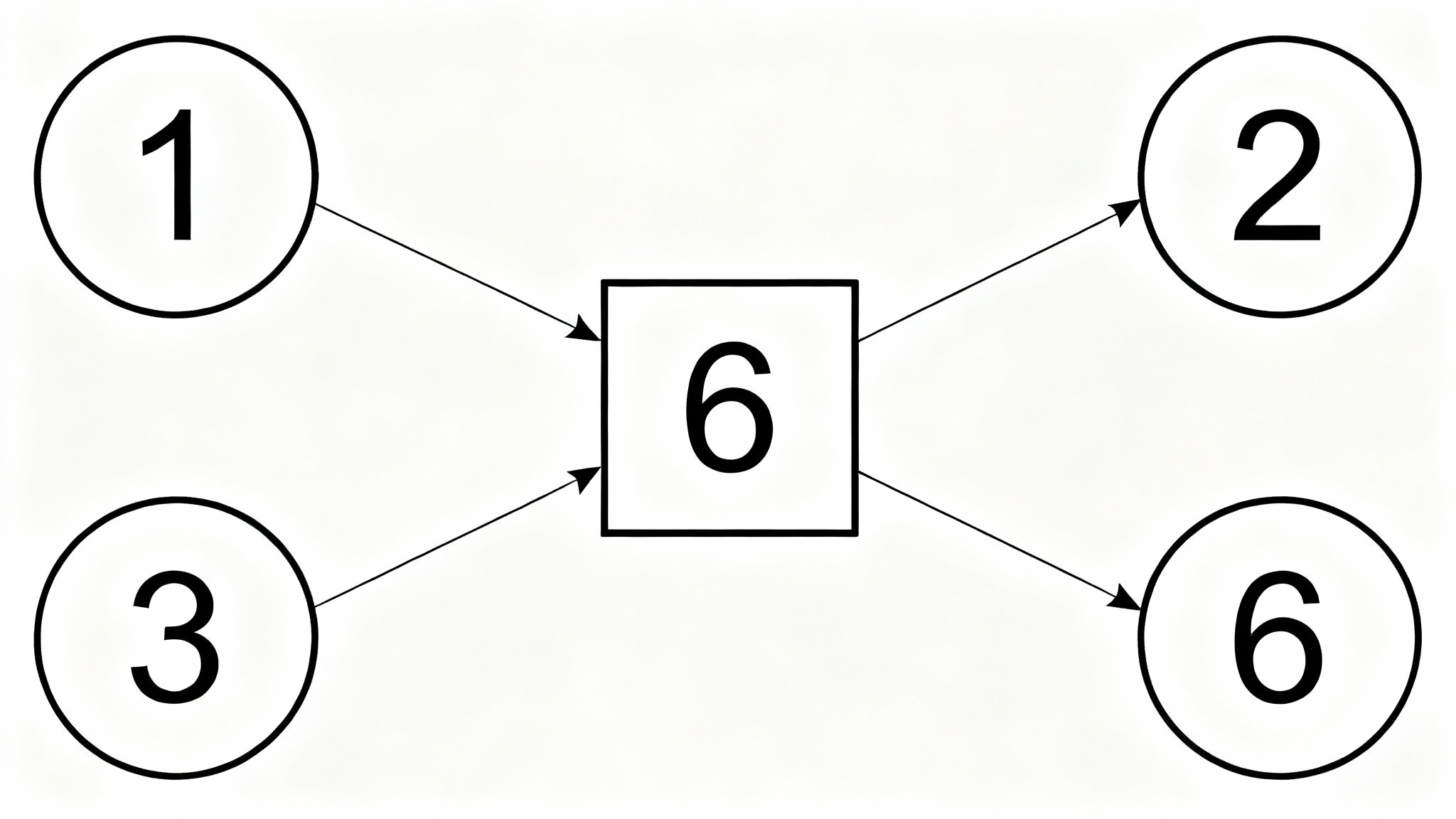
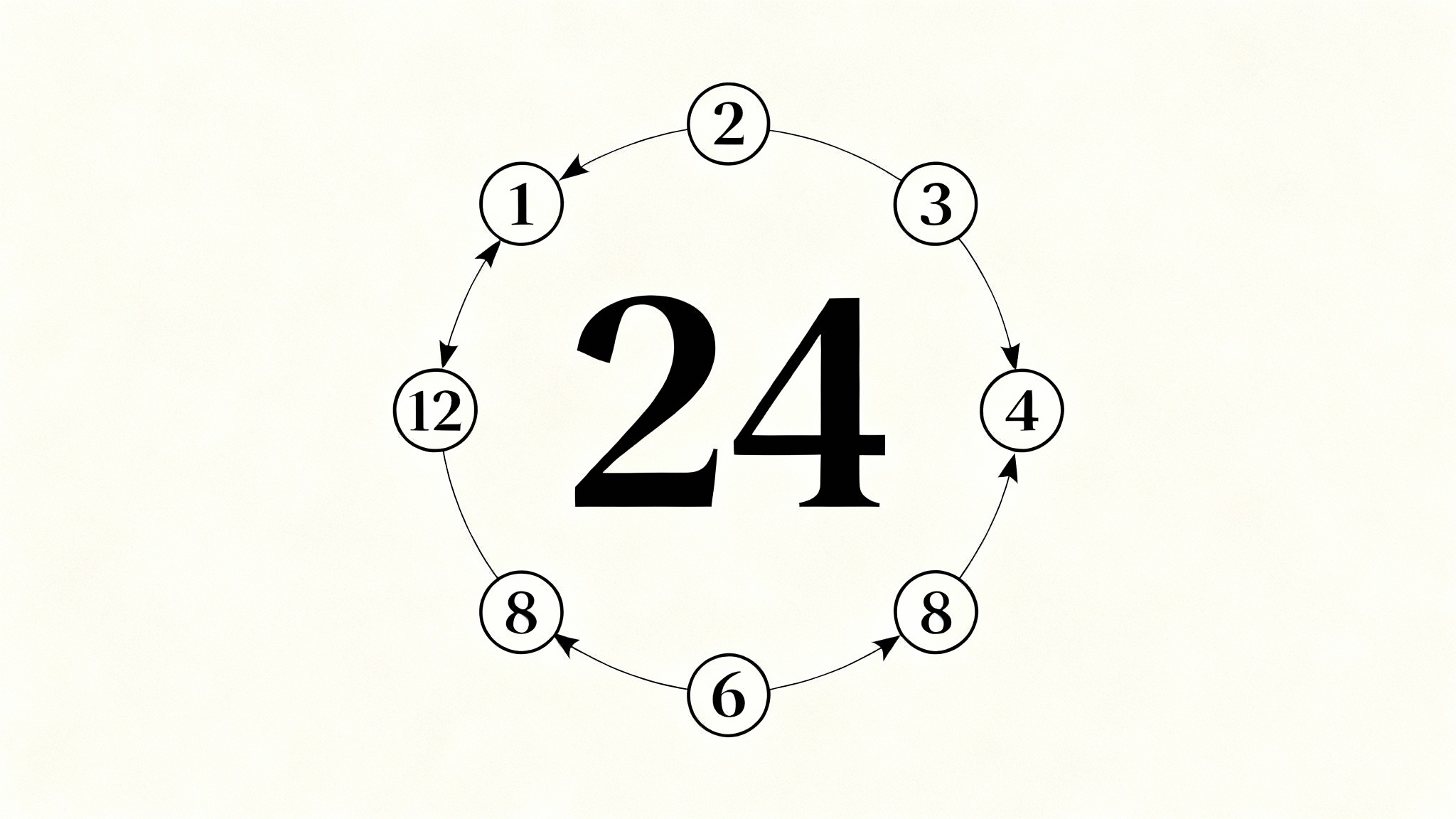
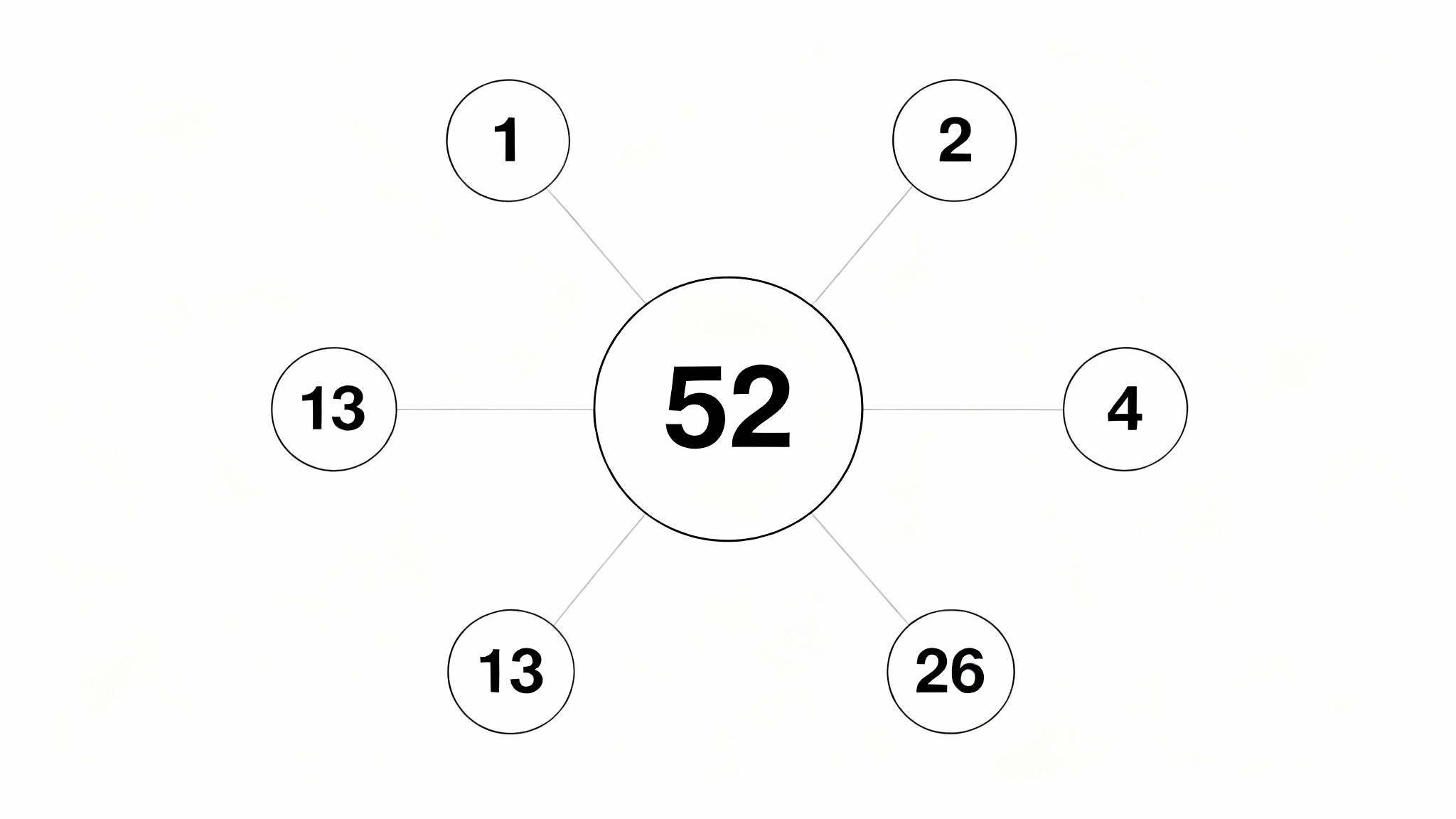
Görsel

14:36:07

AI Öğretmen

Bir sayının pozitif tam sayı çarpanlarını bulmak için, 1’den başlayarak o sayıyı kalansız bölen tüm tam sayılar belirlenir.

14:36:08

AI Öğretmen

52 sayısının çarpanlarını adım adım bulalım.

14:36:11

AI Öğretmen

52'yi 1'e böldüğümüzde sonuç 52 olur, yani 1 ve 52 çarpandır.

14:36:12

AI Öğretmen

52'yi 2'ye böldüğümüzde sonuç 26 çıkar, yani 2 ve 26 da çarpandır.

14:36:13

AI Öğretmen

52, 3'e tam olarak bölünmez, bu yüzden 3 çarpan değildir.

14:36:15

AI Öğretmen

52'yi 4'e böldüğümüzde sonuç 13 olur, böylece 4 ve 13 de çarpandır.

14:36:16

AI Öğretmen

52, 5, 6 ve 7'ye tam bölünmez, bu yüzden bu sayılar da çarpan değildir.

14:36:17

AI Öğretmen

Başka çarpan bulunamaz.

14:36:19

AI Öğretmen

Sonuç olarak, 52 sayısının pozitif tam sayı çarpanları 1, 2, 4, 13, 26 ve 52’dir.

14:36:20

AI Öğretmen

Not: Pratik olarak, sadece $\sqrt{52}$ yani yaklaşık 7,2’ye kadar olan sayılar kontrol edilerek kalan çarpanlar da bulunabilir.

14:36:21

AI Öğretmen

52 sayısının çarpanlarını bulma yöntemini anladın mı?

14:37:08

Öğrenci

Anladım

14:37:12

💭 AI Öğretmen

Şimdi biraz soruya bakalım

14:37:13

❓ Soru medium

Kenar uzunlukları santimetre cinsinden birer pozitif tam sayı olan bir dikdörtgenin alanı $144 \text{ cm}^2$'dir. Bu bilgilere göre, bu dikdörtgenin çevre uzunluğunun alabileceği en büyük değer ile en küçük değerin farkı kaç santimetredir?

14:38:10

Öğrenci

Cevabım: 121

14:38:11

💭 AI Öğretmen

Hemen Bakıyorum

14:38:17

AI Öğretmen

Cevabınız doğru değil, gelin nedenini birlikte inceleyelim.

14:38:25

AI Öğretmen

Alanı 144 cm² olan dikdörtgenin kenar uzunlukları pozitif tam sayılar olduğundan, kenarların 144 sayısının tam bölenleri olması gerekir. Yani kenar çiftlerini 144'ün çarpanları olarak düşünmeliyiz.

14:38:28

AI Öğretmen

144 sayısının çarpan çiftleri: (1,144), (2,72), (3,48), (4,36), (6,24), (8,18), (9,16), (12,12) şeklindedir.

14:38:30

AI Öğretmen

Dikdörtgenin çevresi 2(a+b) formülüyle hesaplanır. En büyük çevre, kenarların toplamının en büyük olduğu çift ile; en küçük çevre ise en küçük toplamı veren çift ile bulunur.

14:38:34

AI Öğretmen

En büyük çevre için (1,144) çifti seçilir: 2 × (1 + 144) = 2 × 145 = 290 cm. En küçük çevre için ise (12,12) çifti seçilir: 2 × (12 + 12) = 2 × 24 = 48 cm.

14:38:35

AI Öğretmen

Bu durumda çevrelerin farkı: 290 - 48 = 242 cm olur.

14:38:36

AI Öğretmen

Muhtemelen çevreyi hesaplarken ya çarpan çiftlerini tam listelemediniz ya da çevre formülünü yanlış kullandınız.

14:38:38

AI Öğretmen

Bu yüzden doğru cevap 242 cm olmalıdır. Bu tür problemlerde çarpanları dikkatlice listelemek ve çevre formülünü doğru uygulamak önemli.

14:38:39

AI Öğretmen

Çalışmalarınıza devam edin, böyle sorularla pratik yaptıkça daha kolay çözeceksiniz!

14:38:40

AI Öğretmen

Derse devam edelim mi?

14:39:49

Öğrenci

Olur, devam edelim

14:39:50

💭 AI Öğretmen

Tamam, bir sonraki konuya geçiyoruz

14:40:00

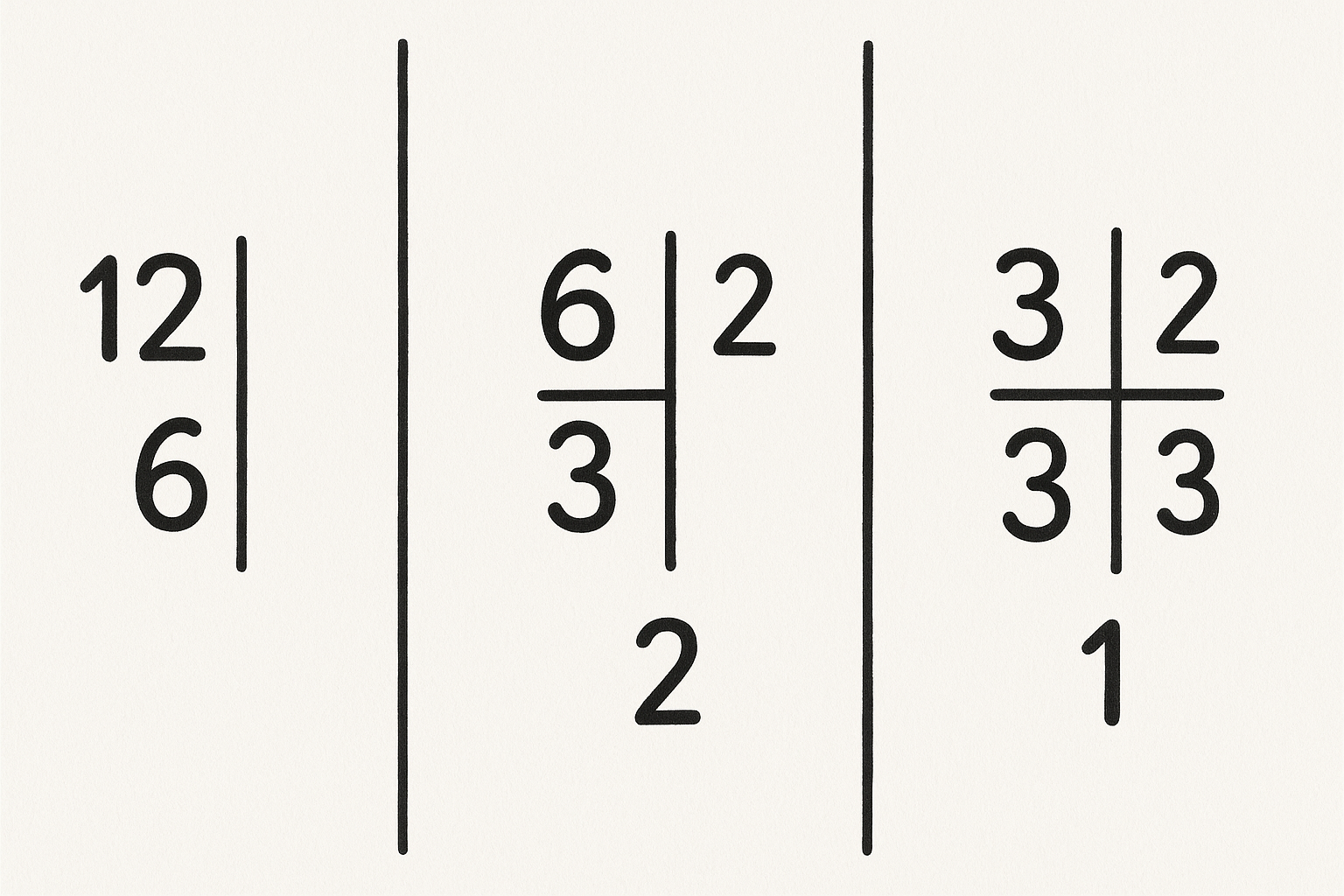
Görsel

14:40:02

AI Öğretmen

Bir sayının pozitif tam sayı çarpanları arasında, kendisi dışında başka pozitif böleni olmayan asal sayılara o sayının asal çarpanları denir.

14:40:03

AI Öğretmen

Asal çarpanlar, verilen sayıyı tam bölen asal sayılardır.

14:40:04

AI Öğretmen

Bir sayının asal çarpanlarını bulmak için en çok kullanılan yöntemlerden biri bölen listesi yöntemidir.

14:40:05

AI Öğretmen

Bölen listesi yönteminin adımlarına bakalım.

14:40:06

AI Öğretmen

Önce, asal çarpanlarına ayırmak istediğimiz sayıyı yazarız ve yanına dik bir çizgi çekeriz.

14:40:08

AI Öğretmen

Sonra, bu sayıyı kalansız bölen en küçük asal sayıyı çizginin sağına yazarız ve bölme işlemine başlarız.

14:40:09

AI Öğretmen

Bulduğumuz sonucu çizginin solundaki sayının altına yazarız.

14:40:10

AI Öğretmen

Sonuç 1 olana kadar aynı işlemi tekrarlayarak her seferinde asal sayılarla böleriz.

14:40:11

AI Öğretmen

Çizginin sağına yazdığımız farklı asal sayıları listeleriz.

14:40:13

AI Öğretmen

Örneğin, 12 sayısı için bölen listesi yöntemi şöyle olur:

14:40:14

AI Öğretmen

İlk olarak 12, 2’ye bölünür ve yanına 2 yazılır, sonuç 6 olur.

14:40:15

AI Öğretmen

6 tekrar 2’ye bölünür ve yine 2 yazılır, sonuç 3 olur.

14:40:16

AI Öğretmen

3, 3’e bölünür ve yanına 3 yazılır, sonuç 1 olur.

14:40:19

AI Öğretmen

Sonuç olarak, asal çarpanları 2, 2 ve 3’tür ve 12 = 2·2·3 şeklinde gösterilir.

14:40:20

AI Öğretmen

Bölen listesi yöntemiyle asal çarpanları bulma sürecini anladın mı?

14:41:13

Öğrenci

Anladım

14:41:15

💭 AI Öğretmen

Şimdi bir soru gelecek

14:41:16

❓ Soru medium

$A$ ve $B$ pozitif tam sayılarının asal çarpanlarına ayrılmış biçimleri aşağıda verilmiştir: $$ A = 2^x \cdot 3^4 \cdot 5^2 $$ $$ B = 2^3 \cdot 3^y \cdot 7^z $$ Bu sayıların en büyük ortak böleni $\text{EBOB}(A, B) = 2^2 \cdot 3^3$ ve en küçük ortak katı $\text{EKOK}(A, B) = 2^3 \cdot 3^4 \cdot 5^2 \cdot 7^5$ olduğuna göre, $x + y + z$ ifadesinin değeri kaçtır?

14:41:49

Öğrenci

Cevabım: 10

14:41:49

💭 AI Öğretmen

Hemen Bakıyorum

14:41:55

AI Öğretmen

Harika bir iş çıkardın! Cevabın kesinlikle doğru!

14:41:56

AI Öğretmen

EBOB ve EKOK'u asal çarpanlarına ayırarak bulma yöntemini çok iyi kavramışsın.

14:41:58

AI Öğretmen

Unutma, EBOB'da ortak asal çarpanların en küçük üslerini alırken, EKOK'ta tüm asal çarpanların en büyük üslerini kullanırız. Bu önemli kuralı başarıyla uyguladın!

14:41:59

AI Öğretmen

Doğru cevap 10'dur.

14:41:59

AI Öğretmen

Derse devam edelim mi?

14:42:17

Öğrenci

Olur, devam edelim

14:42:19

💭 AI Öğretmen

Tamam, devam ediyoruz

14:42:34

AI Öğretmen

Bu derste doğal sayıların çarpanları, pozitif tam sayı çarpanlarının nasıl bulunacağı ve asal çarpanların tanımı ile bölen listesi yöntemi anlatıldı. Ayrıca, 24 ve 52 gibi sayılara örnekler verilerek çarpanların nasıl bulunacağı gösterildi. Anladığın ya da sormak istediğin bir şey var mı?

14:43:01

Öğrenci

Anladım hocam.

14:43:07

AI Öğretmen

Bir sonraki derste görüşmek üzere!

AI Etüt Oturumu

Oturum Bilgileri

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Detaylı Değerlendirme

📜 Oturum Detayları