← Ana Rapor / İPEK DÖNMEZ / Oturum Detayları

AI Etüt Oturumu

Oturum Bilgileri

Başlangıç
21 October 2025, 17:23
Bitiş
Devam ediyor
Süre
39 dakika
Durum
Devam Ediyor

AI Öğretmen Değerlendirmesi

Tespit Edilen Eksikler

Konular:
  • Çarpanlar Ve Katlar
Alt Konular:
  • Pozitif Tam Sayıların Pozitif Tam Sayı Çarpanları
Kazanımlar:
  • Verilen pozitif tam sayıların pozitif tam sayı çarpanlarını bulur, pozitif tam sayıların pozitif tam sayı çarpanlarını üslü ifadelerin çarpımı şeklinde yazar.
  • İki doğal sayının en büyük ortak bölenini (EBOB) ve en küçük ortak katını (EKOK) hesaplar, ilgili problemleri çözer.

Detaylı Değerlendirme

Genel Değerlendirme

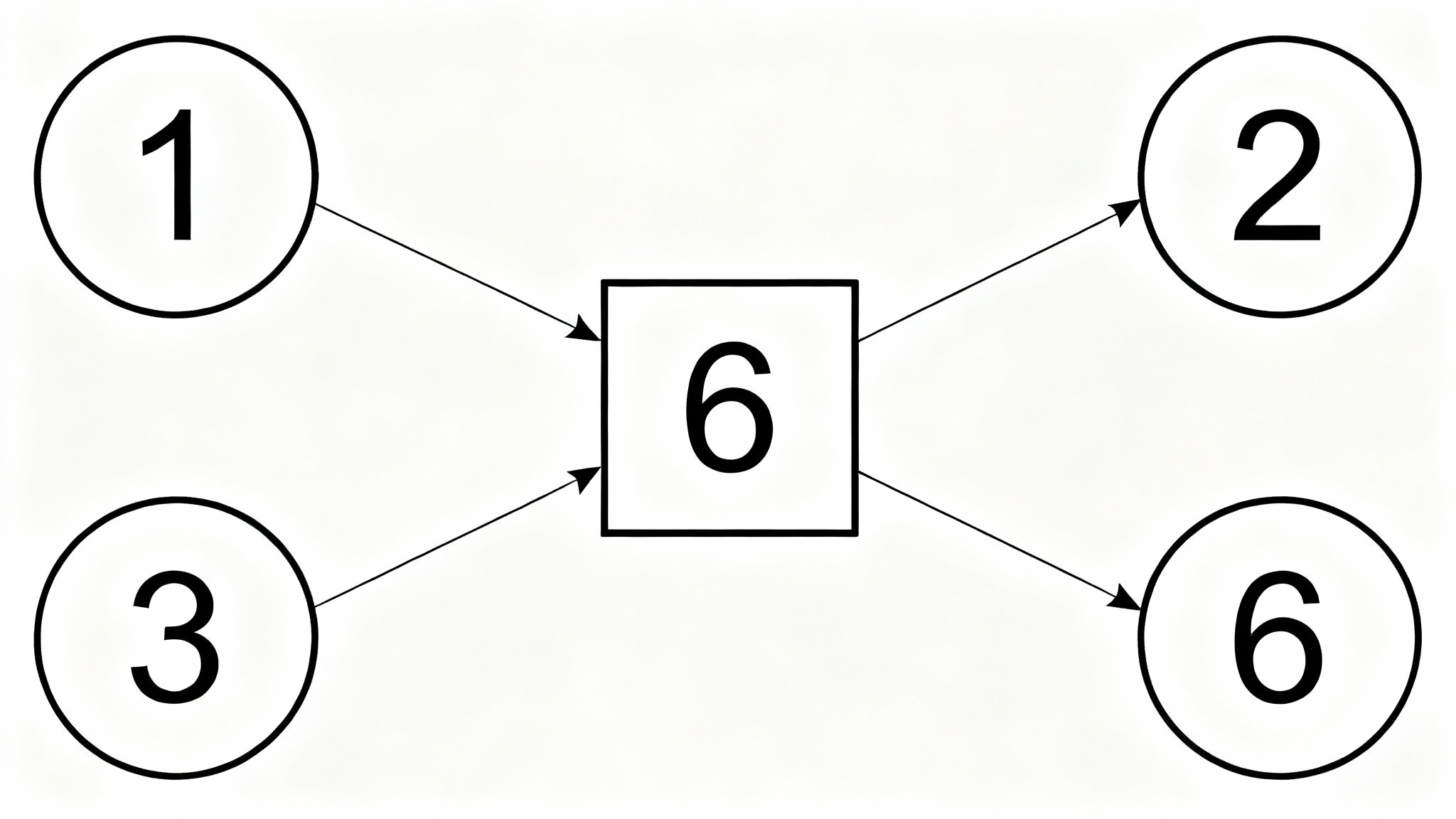
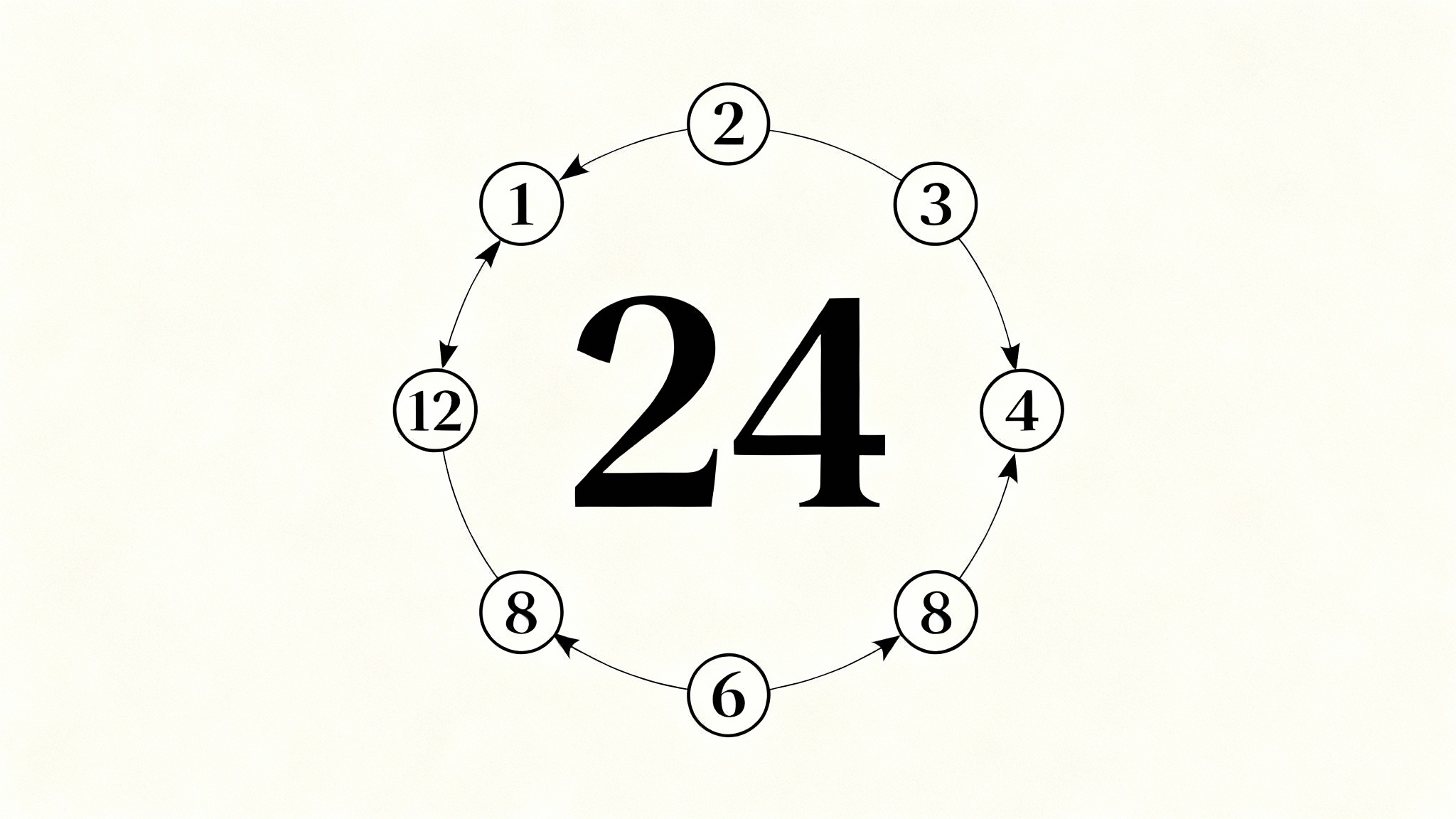
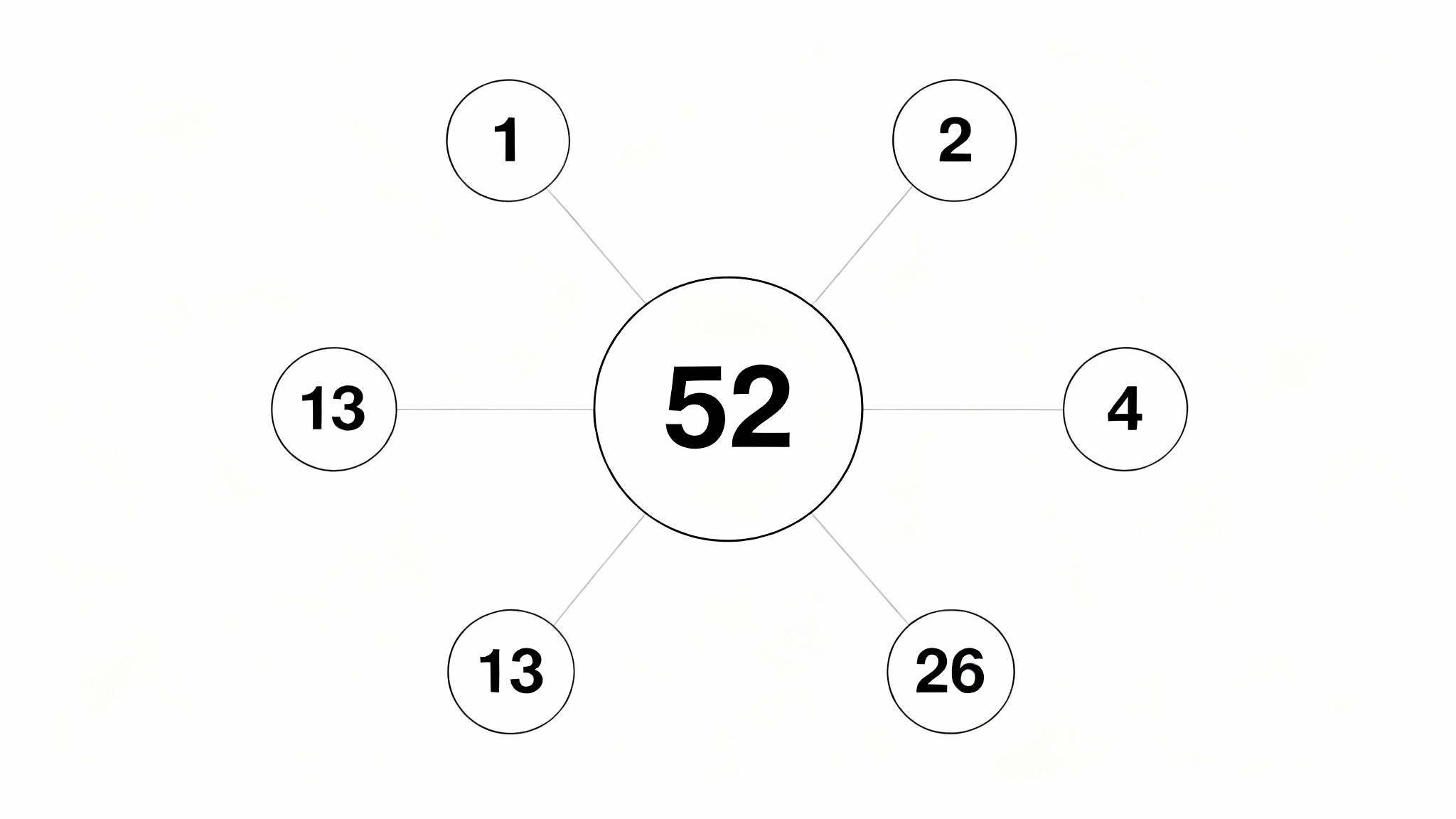
Öğrenci, dersin temel konusu olan pozitif tam sayı çarpanlarını bulma konusunda belirgin zorluklar yaşamaktadır. Ders boyunca, bir sayının tüm çarpanlarını eksiksiz ve doğru bir şekilde listelemesi gereken sorularda (alanı verilen dikdörtgenin çevre uzunluğunu bulma gibi) tekrar tekrar hata yapmıştır. Öğrenci, bazı çarpan çiftlerini bulabilse de genellikle listeyi eksik bırakmakta veya hatalı hesaplamalar yapmaktadır.

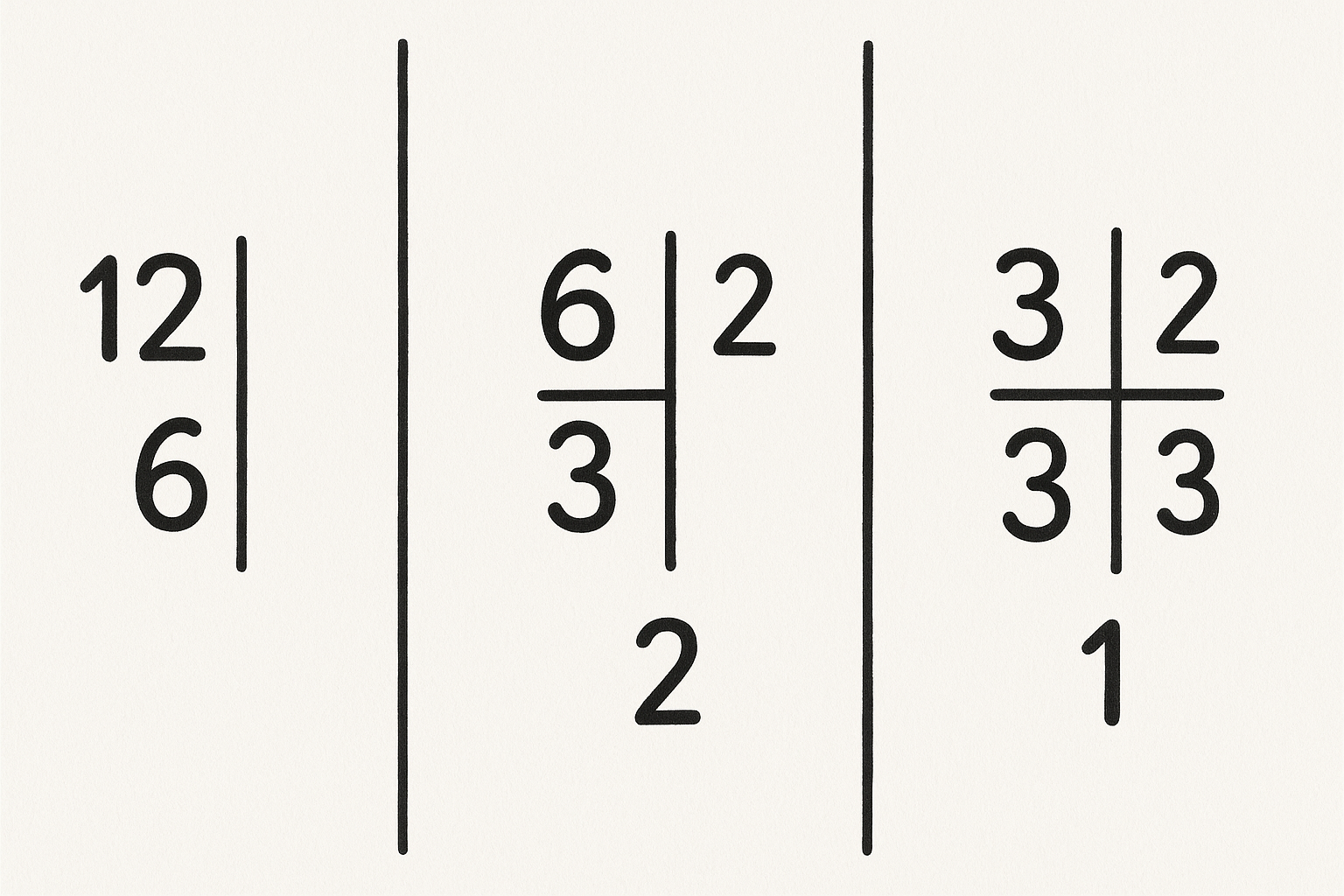
Asal çarpanlara ayırma ve bu yöntemi kullanarak bir sayının pozitif bölen sayısını bulma gibi daha karmaşık konularda temel bilgi eksikliği göze çarpmaktadır. Bu durum, dersin başındaki ilk soruda verdiği tamamen ilgisiz cevapla net bir şekilde görülmüştür.

Öğrencinin olumlu yanı, anlamadığı noktaları sormasıdır ("bu işlemin asal bölen bulma ile farkı nedir" gibi). Bu, öğrenme isteğini göstermektedir. EBOB-EKOK sorusunda ipucu istedikten sonra soruyu doğru çözmesi, konuyu rehberlikle anlayabildiğini ancak tek başına problem çözme konusunda henüz yetkin olmadığını göstermektedir. Dersin sonunda konunun en temel kısmının ("bir sayının doğal sayılarına ayırma") tekrar anlatılmasını istemesi, konunun temel mantığının tam olarak oturmadığını doğrulamaktadır.

Konu Analizi

# Eksiklikler Gözlemlenen Konular (Gaps)

- Konular:
- Çarpanlar Ve Katlar
- Alt Konular:
- Pozitif Tam Sayıların Pozitif Tam Sayı Çarpanları
- Kazanımlar:
- Verilen pozitif tam sayıların pozitif tam sayı çarpanlarını bulur, pozitif tam sayıların pozitif tam sayı çarpanlarını üslü ifadelerin çarpımı şeklinde yazar.
- İki doğal sayının en büyük ortak bölenini (EBOB) ve en küçük ortak katını (EKOK) hesaplar, ilgili problemleri çözer.

# İyi Olduğu Konular (Good At)

Bu derste öğrencinin hiçbir sorun yaşamadan, yardım almadan veya hata yapmadan başarıyla tamamladığı bir konu/kazanım bulunmamaktadır.

Ders Dışı Sorular/Yorumlar

- "hocam yarın bilfen sınavım var sizce en çok hangi soru tipinden çıkar"

📜 Oturum Detayları

17:24:11
Öğrenci
Evet, hazırım Hocam! Bu konuyu detaylıca anlatır mısın?
17:24:11
💭 AI Öğretmen
Tamam, başlıyoruz
17:24:11
Görsel
Görsel
17:24:11
AI Öğretmen
Her doğal sayı, iki doğal sayının çarpımı şeklinde yazılabilir.
17:24:11
AI Öğretmen
Bu şekilde çarpılan iki sayıya, ilgili doğal sayının çarpanları denir.
17:24:11
AI Öğretmen
Bir doğal sayının pozitif tam sayı çarpanları, o sayıyı kalansız bölebilen pozitif tam sayılardır.
17:24:11
AI Öğretmen
Yani, pozitif tam sayı çarpanları aynı zamanda o sayının bölenleridir.
17:24:11
AI Öğretmen
Çarpanlar konusu, bir sayının hangi sayılara bölünebildiğini anlamamıza yardımcı olur.
17:24:11
AI Öğretmen
Örnek olarak; 6 sayısının çarpanları 1, 2, 3 ve 6'dır.
17:24:11
AI Öğretmen
Bu sayılar, 6'yı kalansız bölebilen pozitif tam sayılardır.
17:24:12
AI Öğretmen
Pozitif tam sayıların çarpanlarını bulmak, çarpanlar ve katlar konusunun temelini oluşturur.
17:24:12
AI Öğretmen
Çarpanlar konusu hakkında anlattıklarımı anladın mı?
17:25:39
Öğrenci
Anladım
17:25:39
💭 AI Öğretmen
Şimdi soruya geçelim
17:25:40
❓ Soru medium
$A$ pozitif tam sayısının pozitif tam sayı çarpanlarının sayısı $15$'tir. $A \lt 500$ olduğuna göre, $A$'nın alabileceği tüm değerlerin toplamı kaçtır?
17:27:23
Öğrenci
Cevabım: 1•500 2•250. cevap358 5•100
17:27:23
💭 AI Öğretmen
Kontrol ediyorum
17:27:24
AI Öğretmen
Cevabınız doğru değil, çünkü soruda sayının tam sayı çarpanlarının sayısını bulmak için asal çarpanlarına ayrılması gerektiği gözden kaçmış.
17:27:24
AI Öğretmen
Bir sayının pozitif tam sayı çarpanlarının sayısını bulmak için sayıyı asal çarpanlarına ayırırız. Örneğin, $A = x^a \cdot y^b \cdot z^c \cdot ...$ şeklindeyse, çarpan sayısı $(a+1)(b+1)(c+1)...$ formülüyle hesaplanır.
17:27:24
AI Öğretmen
Soruda, çarpan sayısının 15 olduğu verilmiş. 15 sayısını iki şekilde çarpanlarına ayırabiliriz: 15 (tek asal çarpan kuvveti) veya 3×5 (iki asal çarpanın kuvvetleri).
17:27:24
AI Öğretmen
İlk durumda, $A = x^{14}$ olur ama $2^{14} = 16384$ sayısı 500’den büyük olduğu için bu seçenek uygun değil.
17:27:24
AI Öğretmen
İkinci durumda ise $A = x^4 \cdot y^2$ veya $x^2 \cdot y^4$ şeklinde olabilir. En küçük asal sayılarla denediğimizde 144, 324 ve 400 sayıları 500’den küçük ve çarpan sayısı 15 olan sayılar olarak bulunur.
17:27:24
AI Öğretmen
Örneğin, $2^4 \cdot 3^2 = 16 \times 9 = 144$ sayısı, tam sayı çarpan sayısı $(4+1)(2+1) = 5 \times 3 = 15$ olur.
17:27:24
AI Öğretmen
Sorunun doğru cevabı, $A$'nın alabileceği tüm değerlerin toplamı olan $144 + 324 + 400 = 868$’dir.
17:27:24
AI Öğretmen
Bu nedenle, doğru cevap 868 olmalıdır. Çalışmaya devam et, böylece benzer sorularda daha kolay çözümler bulabilirsin!
17:27:24
AI Öğretmen
Derse devam edelim mi?
17:30:08
Öğrenci
Olur, devam edelim
17:30:08
💭 AI Öğretmen
Devam ediyoruz hemen
17:30:08
Görsel
Görsel
17:30:08
AI Öğretmen
Bir sayının çarpanları, o sayıyı kalansız bölen pozitif tam sayılardır.
17:30:08
AI Öğretmen
24 sayısının çarpanlarını bulmak için çarpan çiftlerini inceleyebiliriz: 1 × 24, 2 × 12, 3 × 8, 4 × 6.
17:30:09
AI Öğretmen
Buradan hareketle, 24'ü kalansız bölen pozitif tam sayılar şunlardır: 1, 2, 3, 4, 6, 8, 12 ve 24.
17:30:09
AI Öğretmen
Bu sayıların her biri, 24'ü başka bir pozitif tam sayı ile çarptığımızda sonucu 24 yapan sayılardır.
17:30:09
AI Öğretmen
Yani, örneğin 2 × 12 = 24 olduğu için hem 2 hem de 12, 24'ün çarpanlarıdır.
17:30:09
AI Öğretmen
Aynı şekilde 3 × 8 = 24 ve 4 × 6 = 24 çarpımlarını da kontrol ederek diğer çarpanları bulabiliriz.
17:30:09
AI Öğretmen
Böylece 24'ü kalansız bölen pozitif tam sayılar 1, 2, 3, 4, 6, 8, 12 ve 24 olur.
17:30:09
AI Öğretmen
24 sayısının çarpanlarını bulma yöntemini anladın mı?
17:32:50
Öğrenci
Anladım
17:32:50
💭 AI Öğretmen
Şimdi bir soru soracağım
17:32:50
❓ Soru medium
Alanı $72$ cm$^2$ olan bir dikdörtgenin kenar uzunlukları, santimetre cinsinden $1$'den büyük birer tam sayıdır. Bu dikdörtgenin çevre uzunluğunun alabileceği kaç farklı tam sayı değeri vardır?
17:36:11
Öğrenci
Cevabım: 1•72 2.36 3•26 cevap6 4•8 6•12 8•9
17:36:12
💭 AI Öğretmen
Kontrol ediyorum
17:36:12
AI Öğretmen
Cevabın doğru değil, çünkü bazı çarpan çiftlerini yanlış yazmışsın ve eksik bırakmışsın. Mesela, $3 \times 26$ diye yazmışsın, oysa doğru çarpan çifti $3 \times 24$ olmalıydı.
17:36:12
AI Öğretmen
Alan $72$ cm$^2$ olduğuna göre, kenar uzunlukları $72$ sayısının tam çarpanları olmalıdır. Ayrıca, kenar uzunlukları $1$'den büyük tam sayılar olmalı, yani $1 \times 72$ çifti uygun değil.
17:36:12
AI Öğretmen
Doğru çarpan çiftleri şunlardır: $(2, 36)$, $(3, 24)$, $(4, 18)$, $(6, 12)$ ve $(8, 9)$.
17:36:12
AI Öğretmen
Şimdi her bir çift için çevre uzunluğunu hesaplamamız gerekiyor. Dikdörtgenin çevresi $2 \times (a + b)$ formülüyle bulunur. Örneğin, $(2, 36)$ için çevre $2 \times (2+36) = 76$ cm olur.
17:36:12
AI Öğretmen
Diğer çevre uzunlukları ise sırasıyla: $54$, $44$, $36$ ve $34$ cm'dir. Böylece toplamda $5$ farklı çevre uzunluğu elde edilir.
17:36:12
AI Öğretmen
Özetle, doğru cevap $5$ farklı tam sayı değeri vardır. Çalışmalarına devam et, böylece daha da iyi anlayacaksın!
17:36:12
AI Öğretmen
Derse devam edelim mi?
17:38:19
Öğrenci
Olur, devam edelim
17:38:19
💭 AI Öğretmen
Hemen bakıyorum
17:38:19
Görsel
Görsel
17:38:20
AI Öğretmen
Bir sayının pozitif tam sayı çarpanlarını bulmak için, 1’den başlayarak o sayıyı kalansız bölen tüm tam sayılar belirlenir.
17:38:20
AI Öğretmen
Şimdi 52 sayısının çarpanlarını adım adım bulalım.
17:38:20
AI Öğretmen
52 ÷ 1 = 52, bu yüzden 1 ve 52 çarpandır.
17:38:20
AI Öğretmen
52 ÷ 2 = 26, bu yüzden 2 ve 26 çarpandır.
17:38:20
AI Öğretmen
52, 3’e tam bölünmez.
17:38:20
AI Öğretmen
52 ÷ 4 = 13, bu yüzden 4 ve 13 çarpandır.
17:38:20
AI Öğretmen
52, 5, 6 ve 7’ye tam bölünmez.
17:38:20
AI Öğretmen
Başka çarpan bulunamaz.
17:38:20
AI Öğretmen
Sonuç olarak, 52 sayısının pozitif tam sayı çarpanları 1, 2, 4, 13, 26 ve 52’dir.
17:38:20
AI Öğretmen
Not: Pratikte, yalnızca √52’ye (yaklaşık 7,2) kadar olan sayılar kontrol edilerek diğer eşleşen çarpanlar da bulunabilir.
17:38:20
AI Öğretmen
52 sayısının pozitif tam sayı çarpanlarını bulma yöntemini anladın mı?
17:38:55
Öğrenci
Anladım
17:38:56
💭 AI Öğretmen
Şimdi bir soru soracağım
17:38:56
❓ Soru medium
Kenar uzunlukları santimetre cinsinden birer pozitif tam sayı olan bir dikdörtgenin alanı $144 \text{ cm}^2$'dir. Bu bilgilere göre, bu dikdörtgenin çevre uzunluğunun alabileceği en büyük değer ile en küçük değerin farkı kaç santimetredir?
17:46:10
Öğrenci
Cevabım: en küçük 9 ve 16 en büyük 2 ve 72 en küçük 50 en büyük 148 148-50=98
17:46:11
💭 AI Öğretmen
Kontrol ediyorum
17:46:11
AI Öğretmen
Cevabınız doğru değil, size nedenini açıklayayım.
17:46:11
AI Öğretmen
Öncelikle, alanı 144 cm² olan dikdörtgenin kenar uzunlukları pozitif tam sayılar olduğuna göre, kenarların çarpımı 144 olmalıdır. Yani, kenar çiftleri 144 sayısının tam sayı çarpanları olmalı.
17:46:11
AI Öğretmen
144'ün tam sayı çarpan çiftleri şunlardır: (1,144), (2,72), (3,48), (4,36), (6,24), (8,18), (9,16), (12,12). Tüm bu çiftleri göz önünde bulundurmalısınız.
17:46:11
AI Öğretmen
Çevre uzunluğu, 2 × (a + b) formülüyle bulunur. En küçük çevre, kenarların birbirine en yakın olduğu çift (12,12) ile, en büyük çevre ise kenarların çok farklı olduğu çift (1,144) ile elde edilir.
17:46:11
AI Öğretmen
Örneğin, (12,12) için çevre 2 × (12 + 12) = 48 cm, (1,144) için çevre 2 × (1 + 144) = 290 cm olur.
17:46:11
AI Öğretmen
Sizin hesaplamalarınızda bazı kenar çiftleri eksik kalmış ve çevre hesaplamalarında da yanlışlıklar var. Böylece en büyük ve en küçük çevre arasındaki farkı yanlış bulmuşsunuz.
17:46:11
AI Öğretmen
Doğru fark, 290 - 48 = 242 cm'dir. Bu yüzden doğru cevap 242 olmalıdır.
17:46:11
AI Öğretmen
Bu tür problemlerde, tüm olası çarpan çiftlerini dikkatlice listelemek ve çevre formülünü doğru uygulamak çok önemli. Bir dahaki sefere daha dikkatli yapacağınıza eminim!
17:46:12
AI Öğretmen
Derse devam edelim mi?
17:48:52
Öğrenci
Olur, devam edelim
17:48:53
💭 AI Öğretmen
Devam ediyorum hemen
17:48:53
Görsel
Görsel
17:48:53
AI Öğretmen
Bir sayının pozitif tam sayı çarpanları arasında, kendisi dışında başka pozitif böleni olmayan asal sayılara o sayının asal çarpanları denir.
17:48:53
AI Öğretmen
Asal çarpanlar, verilen sayıyı tam bölen asal sayılardır.
17:48:53
AI Öğretmen
Bir sayının asal çarpanlarını bulmak için en çok kullanılan yöntemlerden biri bölen listesi yöntemidir.
17:48:53
AI Öğretmen
Bölen listesi yönteminin ilk adımı, asal çarpanlarına ayırmak istediğimiz sayıyı yazar ve yanına dik bir çizgi çekeriz.
17:48:53
AI Öğretmen
İkinci adımda, bu sayıyı kalansız bölen en küçük asal sayıyı çizginin sağına yazar ve bölme işlemini başlatırız.
17:48:53
AI Öğretmen
Üçüncü adımda, elde ettiğimiz sonucu çizginin solundaki sayının altına yazarız.
17:48:53
AI Öğretmen
Dördüncü adımda, sonuç 1 olana kadar aynı işlemi tekrarlayarak her seferinde asal sayılarla böleriz.
17:48:54
AI Öğretmen
Beşinci adımda, çizginin sağına yazdığımız farklı asal sayıları listeleriz.
17:48:54
AI Öğretmen
Örneğin, 12 sayısı için bölen listesi yöntemi şu şekildedir: 12 | 2 → 6.
17:48:54
AI Öğretmen
Sonra 6 | 2 → 3.
17:48:54
AI Öğretmen
Sonra 3 | 3 → 1.
17:48:54
AI Öğretmen
Sonuç olarak, asal çarpanları 2, 2 ve 3 olup, 12 = 2·2·3 şeklinde ifade edilir.
17:48:54
AI Öğretmen
Bu açıklamayı anladın mı?
17:50:12
Öğrenci
bu işlemin asal bölen bulma ile farkı nedir
17:50:12
💭 AI Öğretmen
Güzel soru, hemen bakıyorum
17:50:12
AI Öğretmen
Asal bölen bulma işlemi, bir sayıyı asal sayıların çarpımı şeklinde ifade etmektir ve bölen listesi yöntemi bunun için kullanılan bir tekniktir.
17:50:12
AI Öğretmen
Pozitif tam sayı çarpanlarını bulmak ise, sayıyı kalansız bölen tüm pozitif tam sayıları bulmak anlamına gelir; burada asal olup olmaması önemli değildir.
17:50:12
AI Öğretmen
Yani, asal bölen bulma işlemi sadece asal çarpanlara odaklanırken, pozitif tam sayı çarpanları bulma işlemi sayının tüm bölenlerini içerir.
17:50:12
AI Öğretmen
Bölen listesi yöntemi ise asal bölenleri bulmak için kullanılan sistematik bir yoldur.
17:50:12
AI Öğretmen
Bu farkı anladın mı?
17:50:42
Öğrenci
Anladım
17:50:42
💭 AI Öğretmen
Şimdi soruya geçiyoruz
17:50:43
❓ Soru medium
$A$ ve $B$ pozitif tam sayılarının asal çarpanlarına ayrılmış biçimleri aşağıda verilmiştir: $$ A = 2^x \cdot 3^4 \cdot 5^2 $$ $$ B = 2^3 \cdot 3^y \cdot 7^z $$ Bu sayıların en büyük ortak böleni $\text{EBOB}(A, B) = 2^2 \cdot 3^3$ ve en küçük ortak katı $\text{EKOK}(A, B) = 2^3 \cdot 3^4 \cdot 5^2 \cdot 7^5$ olduğuna göre, $x + y + z$ ifadesinin değeri kaçtır?
17:51:02
Öğrenci
Bir ipucu verir misiniz hocam?
17:51:02
💭 AI Öğretmen
Bir bakalım hemen
17:51:03
AI Öğretmen
EBOB ve EKOK kavramlarında, ortak asal çarpanların üsleri nasıl belirlenir, hatırlıyor musun?
17:51:03
AI Öğretmen
Mesela, EBOB'ta bir asal sayının üssü nasıl seçilir, bunu nasıl ifade edebilirsin?
17:51:03
AI Öğretmen
EKOK'ta ise asal sayıların üsleri nasıl belirlenir, hangi üs alınır?
17:54:49
Öğrenci
Cevabım: x=2 y=3 z=5 cevap10
17:54:49
💭 AI Öğretmen
Kontrol ediyorum
17:54:50
AI Öğretmen
Harika bir iş çıkardın! Cevabın tamamen doğru.
17:54:50
AI Öğretmen
EBOB ve EKOK'u asal çarpanlarına ayırarak bulmak için üsleri doğru bir şekilde karşılaştırdın.
17:54:50
AI Öğretmen
EBOB için ortak asal çarpanların en küçük üslerini, EKOK için ise tüm asal çarpanların en büyük üslerini alarak doğru sonuca ulaştın.
17:54:50
AI Öğretmen
Bu konuyu çok iyi kavramışsın, tebrikler!
17:54:50
AI Öğretmen
Dolayısıyla doğru cevap 10'dur.
17:54:50
AI Öğretmen
Derse devam edelim mi?
17:55:57
Öğrenci
Olur, devam edelim
17:55:57
💭 AI Öğretmen
Hemen devam ediyorum
17:55:58
AI Öğretmen
Bu derste doğal sayıların pozitif tam sayı çarpanlarını ve asal çarpanlarını öğrendik. Ayrıca, bir sayının çarpanlarını bulmak için bölen çiftlerini ve asal çarpanlara ayırma yöntemini inceledik. Anlatılan konularla ilgili herhangi bir sorunuz var mı?
17:57:15
Öğrenci
hocam yarın bilfen sınavım var sizce en çok hangi soru tipinden çıkar
17:57:15
AI Öğretmen
Bilfen sınavında en çok çıkma ihtimali olan soru tipleri genellikle pozitif tam sayıların çarpanlarını bulma, asal çarpanlara ayırma ve EBOB-EKOK hesaplama konularından olur.
17:57:15
AI Öğretmen
Özellikle bir sayının pozitif tam sayı çarpanlarını bulma ve asal çarpanlara ayırma soruları sık sorulur.
17:57:15
AI Öğretmen
Ayrıca, verilen sayının çarpan sayısını bulma veya çarpanlar arasındaki ilişkileri anlama soruları da karşına çıkabilir.
17:57:15
AI Öğretmen
Sınava hazırlanırken bu konulara ağırlık vermeni öneririm.
17:57:15
AI Öğretmen
Bu konuda başka bir sorunun var mı, anladın mı?
18:02:44
Öğrenci
hocam bana birdaha bir sayının doğal sayılarına ayım
18:02:44
AI Öğretmen
Bir sayının doğal sayı çarpanları, o sayıyı kalansız bölen pozitif tam sayılardır.
18:02:44
AI Öğretmen
Örneğin, 6 sayısının çarpanları 1, 2, 3 ve 6'dır çünkü bu sayılar 6'yı tam böler.
18:02:44
AI Öğretmen
Bir sayının çarpanlarını bulmak için, o sayıyı 1'den başlayarak kendisine kadar olan sayılarla bölüp kalansız bölünenleri listeleyebilirsin.
18:02:44
AI Öğretmen
Bu sayede, sayının hangi doğal sayılarla tam bölündüğünü bulmuş olursun.
18:02:45
AI Öğretmen
Konuyu anladın mı, başka bir sorunuz var mı?

Voltran Okul Analiz Sistemi